Grenzrate der Substitution
Die Grenzrate der Substitution ist die Steigung der Indifferenzkurve und gibt das Austauschverhältnis zweier Güter zu einem konstanten Nutzenniveau an. Die GRS definiert in welchen Maße zwei Güter miteinander substituierbar sind, ohne dass sich das Nutzenniveau verändert.
In diesem Artikel schauen wir uns zunächst an wie du die Grenzrate der Substitution berechnen kannst. Anschließend schauen wir uns ein Beispiel an und stellen dar, wie die Formel für die Grenzrate der Substitution zu Stande kommt. Falls du keine Lust hast dir das alles mühsam durchlesen zu müssen, schau dir unser Lernvideo zur Grenzrate der Substitution an!
Inhaltsübersicht
Grenzrate der Substitution berechnen
Zunächst brauchen wir eine Nutzenfunktion
, um die GRS berechnen zu können. Dafür nehmen wir eine Funktion imperfekter Substitute: 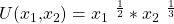 .
.
Für die Grenzrate der Substitution, auf Englisch „Marginal Rate of Substitution“ (MRS) genannt, muss man zunächst den Grenznutzen berechnen. Wie das genau funktioniert und was der Grenznutzen ist, erklären wir dir in unserem Video zum Grenznutzen
. In diesem Fall handelt es sich um einen abnehmenden Grenznutzen. Das siehst du daran, dass sich das Nutzenniveau immer weniger erhöht je mehr du bereits von dem Gut besitzt. Stell dir vor 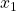 steht hier für Schokolade. Wenn du noch nicht so viel Schokolade gegessen hast, bist du eher bereit mehr für eine weitere Tafel zu zahlen. Wenn du aber bereits sehr viel Schokolade gegessen hast, lässt deine Lust auf eine Weitere nach. Du sprichst der Tafel Schokolade also anfangs einen höheren Nutzen zu.
steht hier für Schokolade. Wenn du noch nicht so viel Schokolade gegessen hast, bist du eher bereit mehr für eine weitere Tafel zu zahlen. Wenn du aber bereits sehr viel Schokolade gegessen hast, lässt deine Lust auf eine Weitere nach. Du sprichst der Tafel Schokolade also anfangs einen höheren Nutzen zu.
Zuerst leitest du die Nutzenfunktion einmal nach 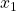 und einmal nach
und einmal nach 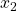 ab. Damit erhältst du die Grenznutzen für Schokolade
ab. Damit erhältst du die Grenznutzen für Schokolade 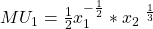 und für Chips
und für Chips 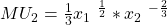 . Um dann die Grenzrate der Substitution auszurechnen musst du nur noch die Grenznutzen durcheinander teilen und ein Minus davor schreiben. Also
. Um dann die Grenzrate der Substitution auszurechnen musst du nur noch die Grenznutzen durcheinander teilen und ein Minus davor schreiben. Also 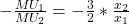 . Wenn du jetzt auch noch Werte für
. Wenn du jetzt auch noch Werte für 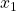 und
und 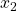 gegeben hast, kannst du durch einsetzten auch schon ein konkretes Austauschverhältnis berechnen.
gegeben hast, kannst du durch einsetzten auch schon ein konkretes Austauschverhältnis berechnen.
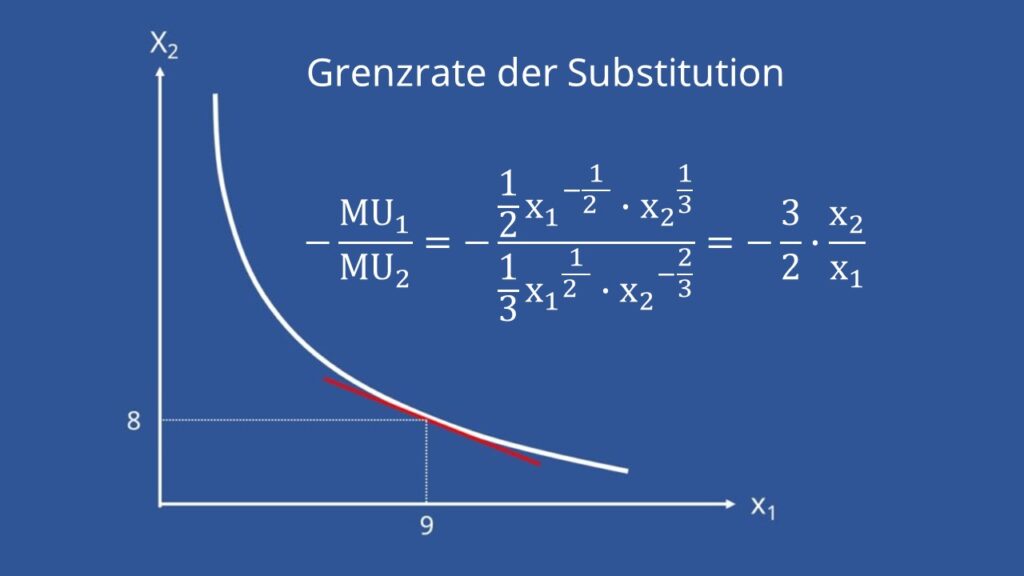
Nehmen wir z.B. an, du hast ein Güterbündel 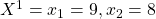 . Das heißt, du besitzt neun Tafeln Schokolade und acht Tüten Chips. Dein Austauschverhältnis wäre dann durch einsetzen, in die ausgerechnete Grenzrate der Substitution
. Das heißt, du besitzt neun Tafeln Schokolade und acht Tüten Chips. Dein Austauschverhältnis wäre dann durch einsetzen, in die ausgerechnete Grenzrate der Substitution 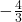 . Du würdest also vier Chipstüten für drei Tafeln Schokolade tauschen.
. Du würdest also vier Chipstüten für drei Tafeln Schokolade tauschen.
Grenzrate der Substitution Beispiel
Klingt erstmal schwer, ist aber eigentlich ganz einfach: Wenn für dich z.B. zwei Tafeln Schokolade genauso viel wert sind wie fünf Tüten Chips, ist dein Austauschverhältnis 2 : 5 bzw. 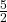 . Die Steigung in diesem Punkt wäre also
. Die Steigung in diesem Punkt wäre also 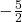 . Die Steigung ändert sich, je nachdem wo sich das Güterbündel auf der Indifferenzkurve befindet. Wichtig ist, dass die Grenzrate der Substitution immer negativ ist, was du an dem fallenden Verlauf der Indifferenzkurve erkennen kannst. Denn Indifferenzkurven sind in der Regel ebenfalls streng monoton fallend.
. Die Steigung ändert sich, je nachdem wo sich das Güterbündel auf der Indifferenzkurve befindet. Wichtig ist, dass die Grenzrate der Substitution immer negativ ist, was du an dem fallenden Verlauf der Indifferenzkurve erkennen kannst. Denn Indifferenzkurven sind in der Regel ebenfalls streng monoton fallend.
Aber wieso hat die Indifferenzkurve eigentlich an unterschiedlichen Punkten eine unterschiedliche Geradensteigung und was bedeutet das für die Grenzrate der Substitution?
Stell Dir vor, du sitzt auf einem Berg Schokolade, hast also viel Schokolade zur Verfügung. Dann bist du gerne bereit, Schokoladentafeln gegen Chips einzutauschen. Hast du von Anfang an aber weniger Schokolade, dann ist deine Bereitschaft zu tauschen gesunken und du willst für eine Tafel Schokolade mehr Chipstüten haben als zuvor. Du hast also in jedem Punkt deiner Kurve eine andere Steigung und damit einen anderen Wert für die Grenzrate der Substitution.
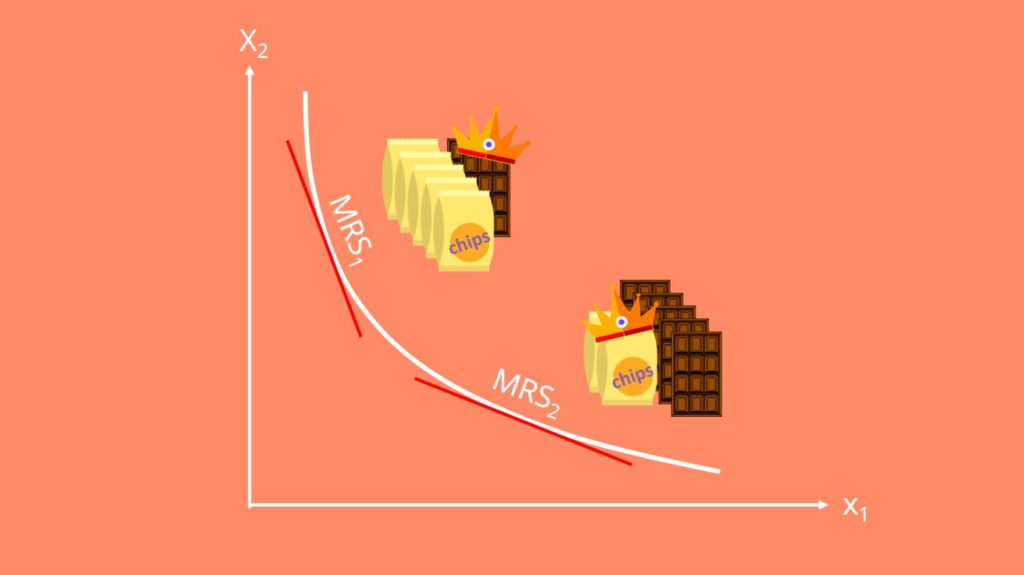
Graphisch schaut das Ganze dann so aus:
Du siehst hier an den roten Tangenten, in welchen Verhältnis du Schokolade und Chips gegeneinander austauschen würdest, um trotzdem noch das gleiche Nutzenniveau zu behalten. Die Grenzrate der Substitution hat damit natürlich in beiden Punkten verschiedene Werte.
Weil du ja im oberen Punkt viel mehr Chipstüten hast, ist Schokolade für dich das knappere Gut und du weist ihr einen höheren Wert zu. Im unteren Punkt ist es genau umgekehrt: hier besitzt du viel weniger Chipstüten als Schokoladentafeln. Du würdest an diesem Punkt also mehr Schokolade für eine weitere Tüte Chips eintauschen.
Grenzrate der Substitution Formel
Um die Grenzrate der Substitution berechnen zu können wird folgende Formel verwendet:
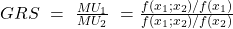
Die Formel der GRS entspricht dem Verhältnis der Grenznutzen der jeweiligen Güter. Dabei wird die Nutzenfunktion nach den Gütern und partiell abgeleitet. Es wird dabei auch von der abnehmenden Grenzrate der Substitution gesprochen.
Zusammenfassung
Die Grenzrate der Substitution: Sie gibt dir das Austauschverhältnis zweier Güter an durch das du auf dem gleichen Nutzenniveau, also auf der gleichen Indifferenzkurve bleibst. Die Grenzrate der Substitution errechnest du einfach indem du die beiden Grenznutzen dividierst und dann die Werte deines Güterbündels einsetzt.