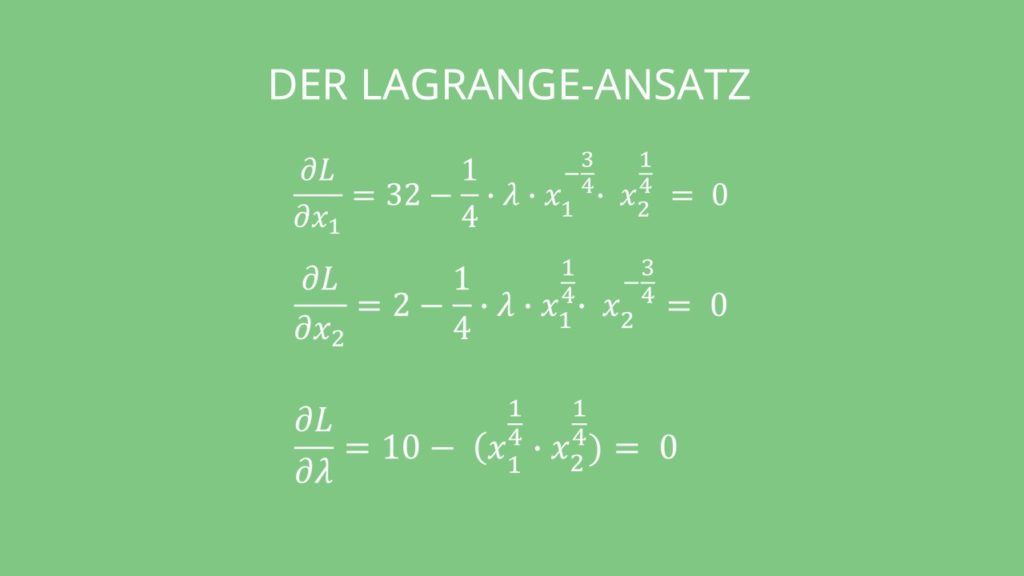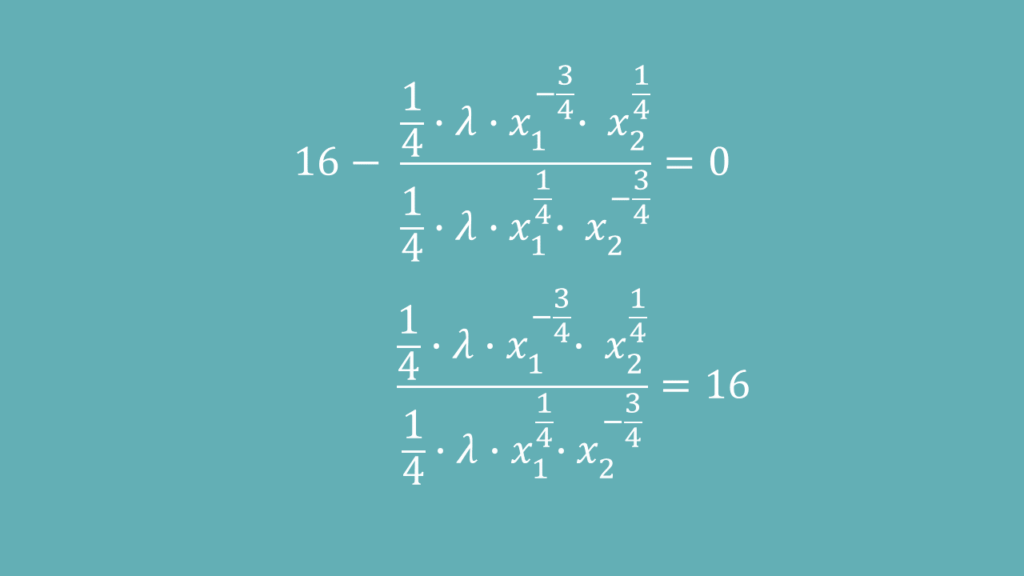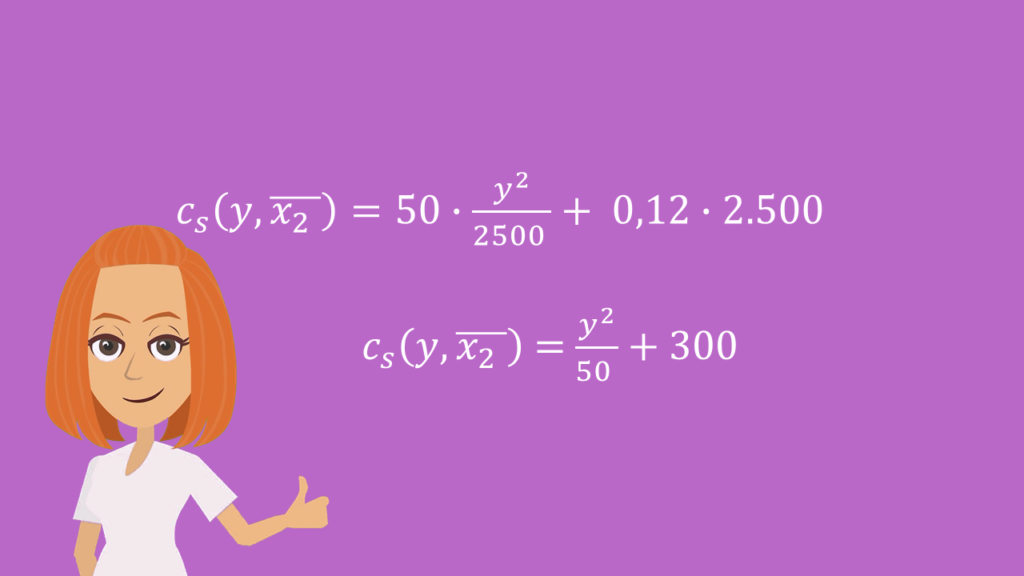Kurz- und langfristige Kostenminimierung
Die Kostenminimierung ist in der Mikroökonomie für Unternehmen besonders wichtig, da sie zu Wettbewerbsvorteilen führt. Die Kostenminimierung wird in langfristig und kurzfristig unterschieden.
Du willst das Ganze abkürzen und ein hochwertiges Video dazu anschauen? Dann klick hier . Denn dort befassen wir uns sowohl mit der langfristigen Kostenminimierung als auch mit der kurzfristigen Kostenminimierung und versuchen dir den Ablauf einfach und verständlich zu erklären.
Inhaltsübersicht
Langfristige Kostenminimierung: Erklärung
Da es hier ja wieder um eine Optimierung auf lange Frist geht, sind auch wieder beide Produktionsfaktoren variabel. Du musst beide Faktoren verändern um Dein Kostenminimum zu erhalten. Machen wir ein Beispiel: Nehmen wir an Du hast ein Unternehmen, das Anzüge produziert. Dann besteht deine Produktion aus Nähmaschinen und Arbeitern. Jetzt willst du die beiden Produktionsfaktoren so kombinieren, dass Du kostenminimal produzierst. Du fragst Dich jetzt bestimmt, wie man das denn berechnen soll? Aber keine Angst, das ist gar nicht so schwer! Fangen wir also am besten gleich an!
Langfristige Kostenminimierung berechnen
Dazu muss erstmal eine Produktionsfunktion
gegeben sein. In unserem Fall 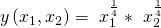 . Die Einsatzmengen von
. Die Einsatzmengen von 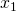 Arbeitern und
Arbeitern und 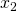 Nähmaschinen sind variabel. Die Preise bzw. Lohnkosten für die Produktionsfaktoren liegen dabei bei
Nähmaschinen sind variabel. Die Preise bzw. Lohnkosten für die Produktionsfaktoren liegen dabei bei 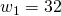 für die Arbeiter
für die Arbeiter 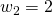 und für die Nähmaschinen. Dazu sollen insgesamt 10 Anzüge produziert werden,
und für die Nähmaschinen. Dazu sollen insgesamt 10 Anzüge produziert werden, 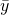 ist also auf 10 festgelegt.
ist also auf 10 festgelegt.
Da wir auch hier wieder eine Nebenbedingung und eine Hauptbedingung haben, benutzen wir den Lagrange-Ansatz. Diesen haben wir ja auch schon bei der Nutzenfunktion verwendet. Wenn du Dir also bei der Anwendung nicht mehr ganz sicher bist, kannst du Dir gerne noch unser Lagrange-Video anschauen!
Hier ist unsere Hauptbedingung die Minimierung der Kostenfunktion. Unsere Nebenbedingung ist das unser Output eine bestimmte Menge erreichen soll. Die Produktion der 10 Anzüge soll also möglichst geringe Kosten verursachen.
Lagrange Ansatz aufstellen:
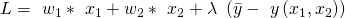
Als nächstes setzen wir die Informationen ein, die wir bereits haben:
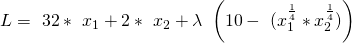
Das leiten wir dann, wie immer, nach allen Variablen einmal ab:
Jetzt teilst du die erste und die zweite Gleichung durcheinander und bringst das Kostenverhältnis der Faktoren auf die andere Seite:
Minimalkostenkombination
Um dann durch Kürzen und Umstellen die Minimalkostenkombination für zu erhalten:
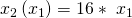
Das war jetzt viel Rechnerei auf einmal, die sich aber gelohnt hat! Denn wir haben auch schon unser erstes Ergebnis: Wir müssen 16 mal so viele Nähmaschinen wie Arbeiter einsetzen.
Das Ganze stellst du nach 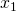 um. Das ergibt dann die Minimalkostenkombination für die Arbeiter
um. Das ergibt dann die Minimalkostenkombination für die Arbeiter
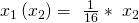 .
.
Die Minimalkostenkombination für setzen wir in die dritte Gleichung ein:
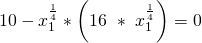
Wenn Du das dann ausrechnest, erhältst Du auch schon einen konkreten Wert für 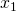 , also die Nähmaschinen:
, also die Nähmaschinen:
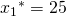
Du solltest also 25 Arbeiter einstellen um Dein langfristiges Kostenminimum zu erreichen. Jetzt brauchst Du nur noch die kostenminimale Anzahl an Nähmaschinen. Dafür setzt Du deinen Wert für 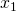 in Deine Minimalkostenkombination von
in Deine Minimalkostenkombination von 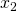 ein. Damit solltest Du also 400 Nähmaschinen in Betrieb nehmen. Schon hast du die Kostenminimierung gemeistert.
ein. Damit solltest Du also 400 Nähmaschinen in Betrieb nehmen. Schon hast du die Kostenminimierung gemeistert.
Langfristige Kostenfunktion
Für die langfristige Kostenfunktion setzt du dann die zugehörige Minimalkostenkombination in die Produktionsfunktion ein und stellst sie nach der passenden Variablen um. Damit erhältst du die konditionalen Faktornachfragen 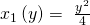 und
und 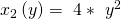 .
.
Wenn Du diese und die Preise der Inputfaktoren in die Kostengleichung 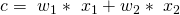 einsetzt, erhältst Du die langfristige Kostenfunktion:
einsetzt, erhältst Du die langfristige Kostenfunktion:
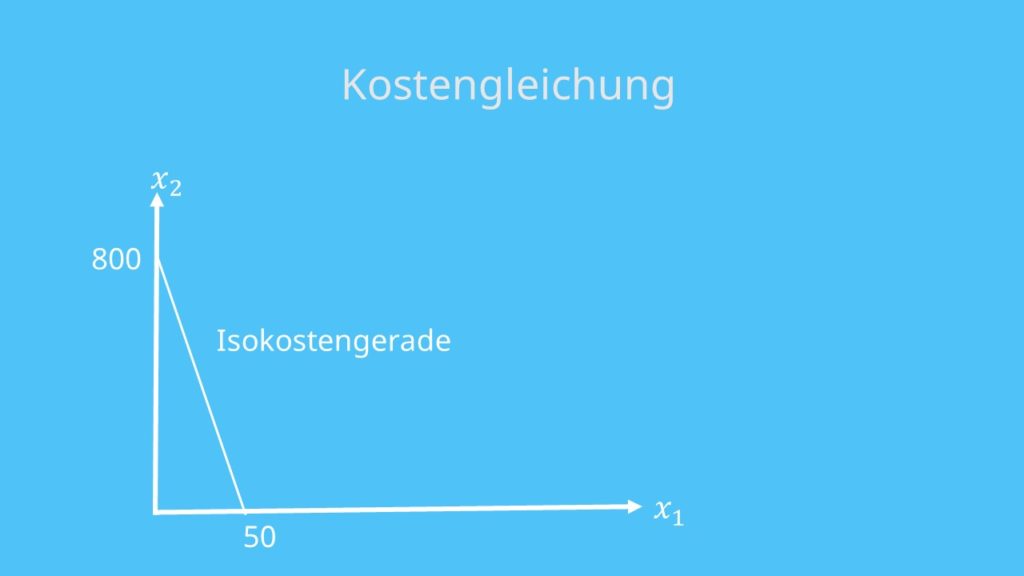
Isokostengerade
Zum Schluss stellen wir noch die Isokostengerade, auch Isokostenlinie genannt, auf. Sie gibt alle Faktor – Mengen – Kombinationen an, welche die gleichen Kosten produzieren. Dafür musst du zunächst Deine Kosten im Kostenminimum ermitteln. Du setzt also Deine kostenminimalen Faktoreinsatzmengen in die Kostengleichung ein:
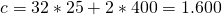
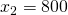 -16
-16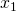
Dein Kostenminimum bei der Produktion von 10 Anzügen beträgt somit 1.600.
Jetzt musst Du nur noch diesen Wert und die Faktorkosten in die Kostengleichung einsetzten und das Ganze nach 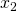 umstellen:
umstellen:
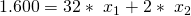
=> 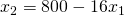
Wir stellen das Ganze nochmal vereinfacht in einer Graphik dar:
Zusammenfassung:
Zunächst stellst du also wieder Deinen Lagrange- Ansatz auf. Dabei ist die Kostengleichung Deine Hauptbedingung, während das Erreichen einer bestimmten Outputmenge Deine Nebenbedingung ist. Dann leitest Du den Lagrange-Ansatz nach allen 3 Variablen ab und teilst die erste durch die zweite Gleichung. Durch umstellen erhältst Du Deine Minimalkostenkombinationen. Die Minimalkostenkombination wird dann in die dritte Gleichung einsetzt. Damit hast Du Deine kostenminimalen Faktoreinsatzmengen. Für die langfristige Kostenkombination musst Du dann nur noch die konditionalen Faktornachfragen in die Kostengleichung einsetzten. Die zuletzt erwähnte Isokostengerade ermittelst Du über das Kostenminimum der gegebenen Outputmenge. Den Wert des Kostenminimums und die Faktorpreise setzt Du dann zum Schluss in Deine Kostengleichung ein und stellst sie nach 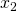 um.
um.
Kurzfristige Kostenminimierung einfach erklärt
Um das Thema der Kostenminimierung abschließen zu können, erklären wir euch im folgenden Abschnitt was genau die kurzfristige Kostenminimierung bedeutet.
Bei der kurzfristigen Kostenminimierung wird, genau wie in der kurzfristigen Gewinnmaximierung, ein Faktor konstant gehalten. Deswegen erklären wir Dir das am besten nochmal am gleichen Beispiel: In der kurzen Frist muss z.B. die Miete für eine Produktionshalle immer gezahlt werden, egal ob die Halle genutzt wird oder nicht. Langfristig kann man dann aber entscheiden ob man die Halle weiterhin mieten möchte.
Der 2. Faktor ist bei der kurzfristigen Produktionsfunktion variabel. Ein Beispiel hierfür wäre die Heizung für die Produktionshalle. Die Halle muss natürlich nur geheizt werden, wenn sie genutzt wird. Der Inputfaktor fällt also nur dann an.
Kurzfristige Kostenminimierung Beispiel
Wir haben zunächst wieder eine Produktionsfunktion 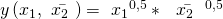 gegeben. Du siehst, dass hier der 2. Faktor, in unserem Fall beispielsweise Kapital, festgesetzt ist. Wir haben hier also einen konkreten Wert gegeben:
gegeben. Du siehst, dass hier der 2. Faktor, in unserem Fall beispielsweise Kapital, festgesetzt ist. Wir haben hier also einen konkreten Wert gegeben: 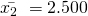 . Jetzt brauchen wir noch einen Preis für das Kapital: sagen wir
. Jetzt brauchen wir noch einen Preis für das Kapital: sagen wir 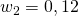 . Das könnten bspw. Opportunitätskosten sein. Du fragst dich, warum Opportunitätskosten? Naja, wenn Du für Dein Kapital in Deinem Unternehmen keine Verwendung hast und es stattdessen zur Bank bringst, erhältst Du Zinsen. Dir entgeht also zusätzliches Geld.
. Das könnten bspw. Opportunitätskosten sein. Du fragst dich, warum Opportunitätskosten? Naja, wenn Du für Dein Kapital in Deinem Unternehmen keine Verwendung hast und es stattdessen zur Bank bringst, erhältst Du Zinsen. Dir entgeht also zusätzliches Geld.
Der Lohnsatz ist in unserem Beispiel auf 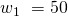 festgelegt.
festgelegt.
So, jetzt haben wir alle Informationen zusammen, die wir brauchen! Legen wir also los!
Dazu stellen wir zunächst den Minimierungsansatz unserer Kosten auf:
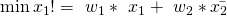
Oder einfach gesagt, wir minimieren unsere Kosten über die allgemeine Kostenfunktion.
Nun stellen wir unsere Produktionsfunktion nach 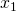 um, damit wir das dann in die Kostenfunktion einsetzen können:
um, damit wir das dann in die Kostenfunktion einsetzen können:
Dann stellen wir unsere allgemeine Kostenfunktion, die von y und 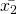 abhängig ist, auf:
abhängig ist, auf:
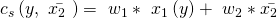
Wie Du siehst, besteht die kurzfristige Kostenfunktion aus variablen Kosten für die Löhne der Arbeiter und Fixkosten für das Kapital.
Nun setzten wir alle unsere Informationen in die Kostenfunktion ein:
Für die kurzfristige Kostenminimierung müssten wir also in unserem Unternehmen diese Kostenfunktion anwenden.
Nun weißt du bescheid was die kurzfristige Kostenminimierung und die langfristige Kostenminimierung bedeutet. Wie nun die Gewinnmaximierung funktioniert, kannst dir in den folgenden Videos anschauen: langfristige Gewinnmaximierung, kurzfristige Gewinnmaximierung.