Nutzenfunktion und Indifferenzkurve
Eine Nutzenfunktion beschreibt alle möglichen Faktorkombinationen zu einem bestimmten Nutzenniveau. In der Mikroökonomie wird sie als Indifferenzkurve dargestellt.
In diesem Artikel stellen wir die unterschiedlichen Arten von Nutzenfunktionen dar und zeigen wie man die Indifferenzkurve zeichnet. Dabei stehen vor allem die Indifferenzkurve von perfekten Komplementen, perfekten Substituten und imperfekten Substituten im Mittelpunkt. Eine graphisch anschaulichere Erklärung erhältst du in unserem Video zur Nutzenfunktion und Indifferenzkurve .
Inhaltsübersicht
Nutzenfunktion und Indifferenzkurve: Perfekte Substitute, perfekte Komplemente und imperfekte Substitute
Beginnen wir zunächst mit der allgemeinen Bedeutung von Nutzenfunktionen und Indifferenzkurven. Die Nutzenfunktion wird in der Volkswirtschaft verwendet, um die Präferenzen der Wirtschaftssubjekte darzustellen. Im Grunde beschreibt sie also, ob und in welchem Ausmaß du ein Gut lieber konsumierst als das andere.
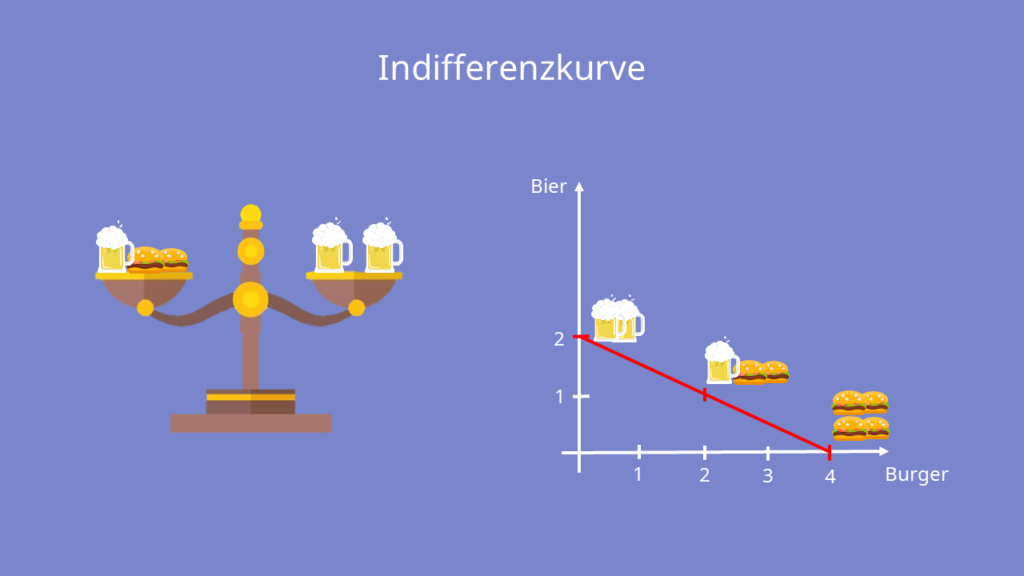
Da könnte also z.B. stehen, dass du für jedes Bier, das du trinkst, gerne zwei Burger verdrücken würdest. Deine Präferenz wäre also zwei Burger für ein Bier. Wenn Du die Nutzenfunktion umstellst, hast Du meist auch schon die passende Indifferenzkurve – dazu aber gleich mehr. Je nach Funktion kann es sich auch um eine lineare, indirekte oder konkave Nutzenfunktion handeln. In der VWL schauen wir uns genauer die speziellen Nutzenfunktionen von perfekten Komplementen, perfekten Substituten und imperfekten Komplementen an.
Indifferenzkurve Definition
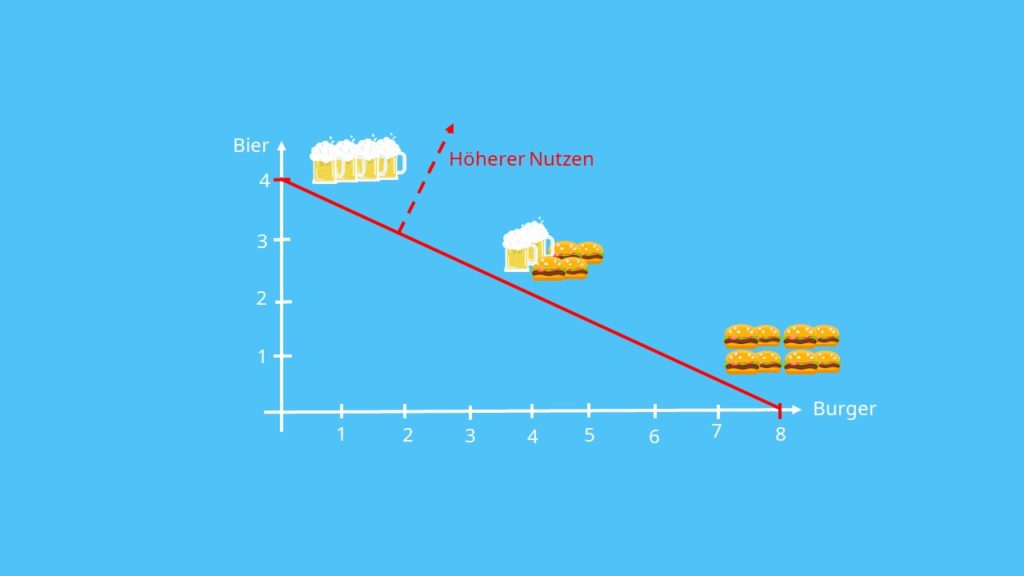
Die Indifferenzkurve wird auch häufig als Iso-Nutzenfunktion, Iso-Nutzenkurve oder Nutzen-Isoquante bezeichnet. Sie stellt dar, welche Güter-Mengen-Kombinationen Dir den gleichen Nutzen bringen. Auf einer Indifferenzkurve bleibt das Nutzenniveau also immer gleich. Wenn Du Dich auf einer Indifferenzkurve entlang bewegst, ändert sich zwar die Kombination Deiner Güter, aber nicht Dein Nutzenniveau. Je weiter die Indifferenzkurve vom Ursprung entfernt ist, desto höher ist dein Nutzen.
Indifferenzkurve zeichnen
Gegebene Nutzenfunktionen lassen sich als Indifferenzkurve zeichnen. Dafür berechnet man zunächst verschiedene Güterbündel zu einem konstantem Nutzenniveau und trägt die Güterkombinationen in ein Diagramm ein. Du stellst dafür im ersten Schritt die Nutzenfunktion nach x2 um. Im zweiten Schritt musst du für eine bestimmtes Nutzenniveau Gütermengenkombinationen berechnen. Anschließend werden die einzelnen Güterkombinationen mit demselben Nutzenniveau zu einer Indifferenzkurve verbunden. Auf Grund der verschiedenen Güterbündeln lassen sich Werte in das Koordinatensystem eintragen. Dadurch kannst du die Indifferenzkurve schnell bestimmen und zeichnen. Anhand unseres Beispiels ist lässt sich das so darstellen:
Nutzenfunktion Beispiel: Perfekte Substitute
Insgesamt gibt es drei Typen von Nutzenfunktionen und ihren dazugehörigen Indifferenzkurven: perfekte Substitute, perfekte Komplemente und imperfekte Substitute.
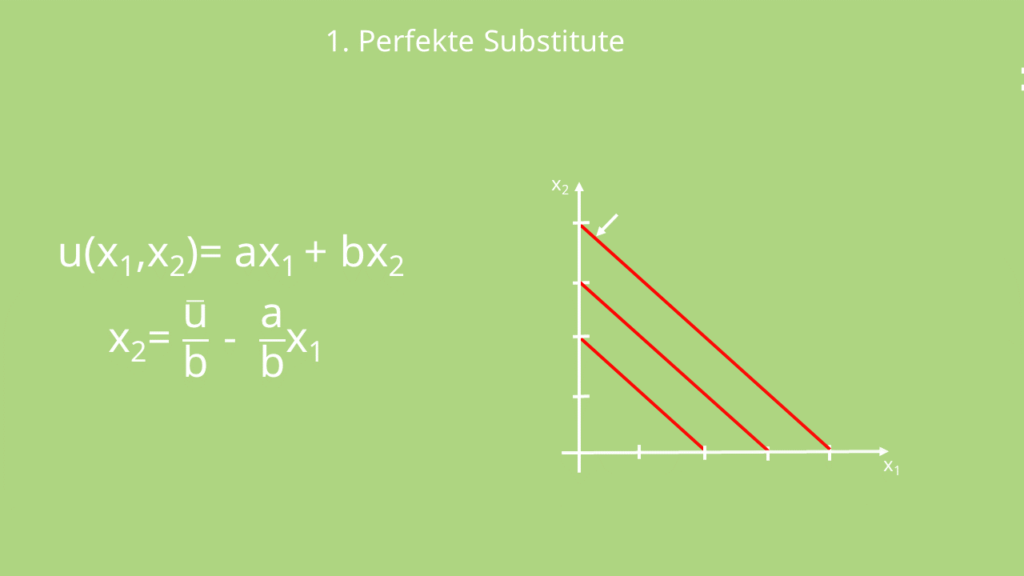
Als erstes nehmen wir uns die Nutzenfunktion der perfekten Substitute vor. Die wichtigste Eigenschaft der perfekten Substitute ist, dass sie beliebig miteinander austauschbar sind. Als Beispiel kann man hier rote und grüne Äpfel nehmen. Beide bringen Dir den gleichen Nutzen, egal ob der Apfel nun rot oder grün ist. Die Nutzenfunktion lautet hier:
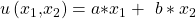
Perfekte Substitute sind also immer additiv miteinander verbunden. Wenn Du das Ganze dann nach 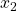 umstellst, hast Du auch schon die passende Indifferenzkurve. Das U mit dem Strich darüber bedeutet einfach, dass hier der Nutzen festgesetzt bzw. konstant ist. Die Steigung
umstellst, hast Du auch schon die passende Indifferenzkurve. Das U mit dem Strich darüber bedeutet einfach, dass hier der Nutzen festgesetzt bzw. konstant ist. Die Steigung 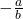 repräsentiert das Austauschverhältnis der beiden Güter.
repräsentiert das Austauschverhältnis der beiden Güter.
Graphisch sieht die Nutzenfunktion dann so aus:
Du siehst bestimmt schon, dass sich das Nutzenniveau auf der Geraden nicht ändert, egal ob du jetzt mehr rote 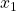 oder grüne
oder grüne 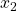 Äpfel hast.
Äpfel hast.
Perfekte Komplemente
Perfekte Komplemente lassen sich ebenfalls als Indifferenzkurve darstellen. Wie der Namen eigentlich schon verrät, vervollständigen sich hier beide Güter. Wenn Du Dir das anhand Drucker 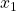 und Druckerpatrone
und Druckerpatrone 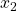 vor Augen führst, verstehst Du die Bedeutung vielleicht schon besser. Sowohl der Drucker als auch die Patrone bringen Dir alleine nichts, da sie sich in ihrem Nutzen ergänzen. Die Nutzenfunktion für perfekte Komplemente ist eine sogenannte Minimum- Funktion und lautet:
vor Augen führst, verstehst Du die Bedeutung vielleicht schon besser. Sowohl der Drucker als auch die Patrone bringen Dir alleine nichts, da sie sich in ihrem Nutzen ergänzen. Die Nutzenfunktion für perfekte Komplemente ist eine sogenannte Minimum- Funktion und lautet:
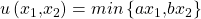
Sie heißt deswegen Minimum-Funktion, da jedes Komplement ein Gegenstück braucht. Dir nutzt es also nichts, wenn du nur einen Drucker, aber dafür 20 Patronen hast. Das bedeutet, Dein Nutzen besteht dann nur aus einem Drucker und einer Patrone. Die restlichen 19 Patronen bringen Dir – zumindest im Augenblick – nichts.
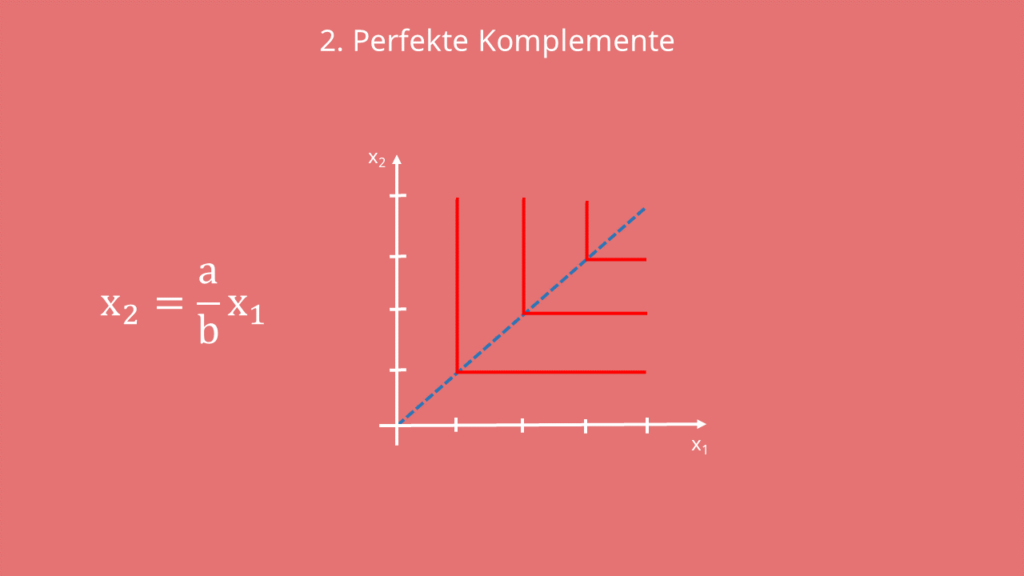
Da hier die Indifferenzkurven nicht explizit darstellbar sind, werden die Mengen der beiden Güter stets im Verhältnis 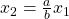 miteinander kombiniert. Das kannst Du Dir also leider nicht rechnerisch herleiten, sondern musst es Dir einfach merken. Aber das ist ja zum Glück keine so komplizierte Gleichung! Graphisch kann die Nutzenfunktion dann so aussehen:
miteinander kombiniert. Das kannst Du Dir also leider nicht rechnerisch herleiten, sondern musst es Dir einfach merken. Aber das ist ja zum Glück keine so komplizierte Gleichung! Graphisch kann die Nutzenfunktion dann so aussehen:
Auf der gepunkteten Linie hast du also von jedem Gut genau gleich viel. Sobald Du von z.B. Patronen 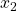 mehr als von Druckern
mehr als von Druckern 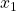 hast, bewegst Du Dich zwar auf der Indifferenzkurve nach oben, Du verlässt sie aber nicht. Dein Nutzenniveau bleibt also gleich.
hast, bewegst Du Dich zwar auf der Indifferenzkurve nach oben, Du verlässt sie aber nicht. Dein Nutzenniveau bleibt also gleich.
Indifferenzkurve berechnen: Imperfekte Substitute
So, jetzt sind wir auch schon bei der letzten Nutzenfunktion angelangt! Das sind die imperfekten Substitute. Bei ihnen handelt es sich um Güter, die einen ähnlichen Nutzen bringen, sich aber in Preis, Qualität oder anderen Merkmalen unterscheiden. Gute Beispiele wären etwa normale und elektronische Bücher, sogenannte E-Books. Beide kannst du lesen, aber vielleicht bevorzugst du auf Papier zu lesen, weil der Akku in deinem Tablet ständig leer geht.
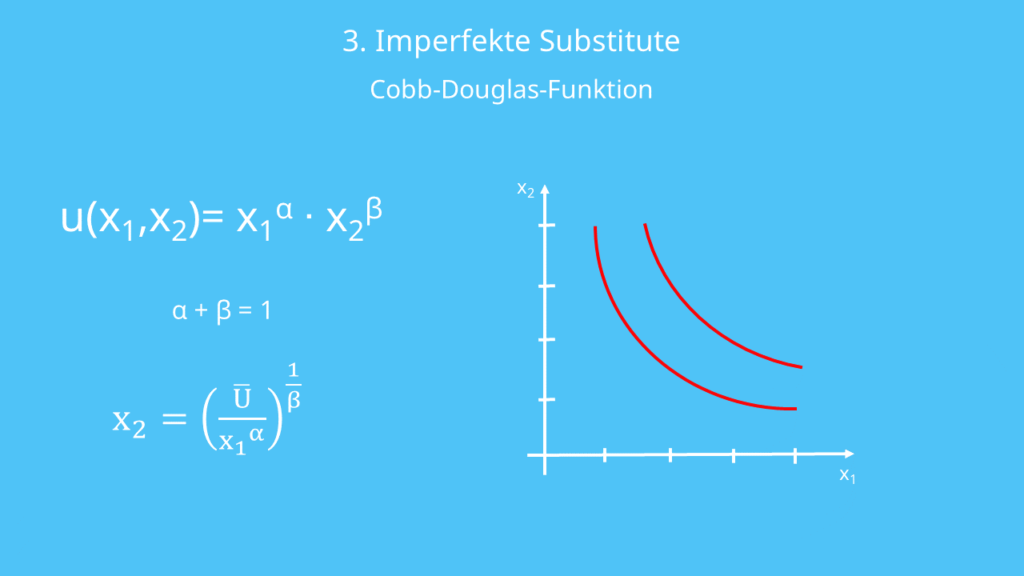
Die gängigste Form für imperfekte Substitute ist die Cobb-Douglas-Funktion , die durch die folgende Gleichung dargestellt wird:
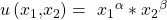
Eine wichtige Eigenschaft von Cobb-Douglas-Funktionen ist, dass sich Alpha und Beta zu 1 addieren lassen bei konstanten Skalenniveaus. Wenn Du das wiederum nach 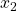 umstellst, hast Du hier auch schon wieder die zugehörige Indifferenzkurve:
umstellst, hast Du hier auch schon wieder die zugehörige Indifferenzkurve:
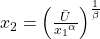
Die Formel sieht jetzt vielleicht etwas kompliziert aus, aber du siehst, es ist nicht schwer eine Nutzenfunktion in eine Indifferenzkurve umzuschreiben. Zur Verdeutlichung haben wir auch hier wieder eine Graphik von der Nutzenfunktion für Dich:
Du siehst bestimmt schon, dass sich das Nutzenniveau auf der Geraden nicht ändert, egal ob du jetzt mehr rote oder grüne Äpfel hast.
Zusammenfassung
Damit Du Dir das auch gut merken kannst, haben wir für Dich nochmal die wichtigsten Fakten zusammengefasst: In der Haushaltstheorie gibt es 3 verschiedene Nutzenfunktionen: Die erste ist die Nutzenfunktionen der perfekten Substituten. Sie repräsentiert Güter, deren Nutzen sich nicht unterscheiden und die austauschbar sind. Die zweite Form ist die der perfekten Komplemente, sie ergänzen sich, sind alleine aber nicht nutzbar. Die dritte und letzte Form ist die der imperfekten Substitute. Das sind Güter, die einen ähnlichen Nutzen haben, sich aber in bestimmten Merkmalen unterscheiden.