Preisdiskriminierung 1. Grades
Im folgenden Beitrag gehen wir auf die verschiedenen Grade der Preisdiskriminierung ein. Anhand einiger Beispiel soll deutlich werden wie die Preisdiskriminierung im Monopol von statten gehen kann.
Heute mal keine Lust aus wissenschaftliche Literatur? Dann schau dir doch einfach unser Video zur Preisdiskriminierung an!
Inhaltsübersicht
Preisdiskriminierung Definition
Die Preisdiskriminierung ist in der Mikroökonomie eine Preispolitik von monopolistischen Anbietern, unterschiedliche Preise für das gleiche Produkt zu verlangen. Man unterscheidet zwischen drei Arten der Diskriminierung: Preisdiskriminierung 1. Grades, Preisdiskriminierung 2. Grades und Preisdiskriminierung 3. Grades. Durch unterschiedliche Preissetzung kann der Monopolist seinen Gewinn maximieren.
Preisdiskriminierung 1. Grades erklärt
Beginnen wir mit der Preisdiskriminierung 1. Grades. Hier kann ein Unternehmer die maximale Zahlungsbereitschaft all seiner Kunden abschöpfen. Deswegen wird sie auch perfekte Preisdiskriminierung genannt. Wenn Du also von Deinem Limonaden-Start-Up ausgehst, dann heißt das, dass Du von jedem Deiner Kunden, gemessen an seiner individuellen Zahlungsbereitschaft, einen anderen Preis verlangst.
Gewinnmaximierende Produktionsmenge
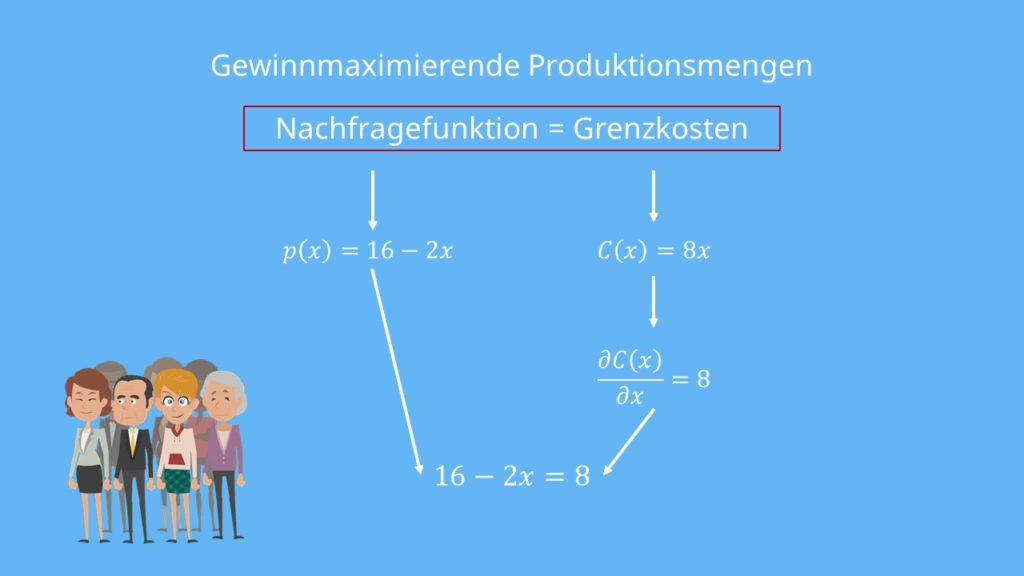
Damit du verstehst, wie das in der Praxis aussieht, berechnen wir die gewinnmaximierenden Produktionsmengen:
Wie vorhin erwähnt, hast Du hier verschiedene Kunden, bei denen Du immer ihre maximale Zahlungsbereitschaft abschöpfst. Wir haben eine Nachfragefunktion 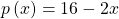 und Kosten mit
und Kosten mit 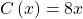 gegeben. Für die Gewinnmaximierung bei der Preisdiskriminierung 1. Grades müssen wir die Grenzkosten mit der Nachfragefunktion gleichsetzen.
gegeben. Für die Gewinnmaximierung bei der Preisdiskriminierung 1. Grades müssen wir die Grenzkosten mit der Nachfragefunktion gleichsetzen.
Um die Grenzkosten zu ermitteln, müssen wir aber zuerst die Kostenfunktion nach x ableiten:
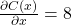
Wir haben also Grenzkosten von 8. Diese setzen wir dann mit der Nachfragefunktion gleich:
Stellst Du die Gleichung nach 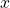 um, ist die gewinnmaximierende Menge 4. Wenn Du die Preisdiskriminierung 1. Grades betreibst und deinen Gewinn maximieren willst, musst Du also 4 Flaschen Limonade produzieren. Diese Menge benötigen wir später nochmal zur Berechnung des Gewinns.
um, ist die gewinnmaximierende Menge 4. Wenn Du die Preisdiskriminierung 1. Grades betreibst und deinen Gewinn maximieren willst, musst Du also 4 Flaschen Limonade produzieren. Diese Menge benötigen wir später nochmal zur Berechnung des Gewinns.
Festlegung Gesamtpreis
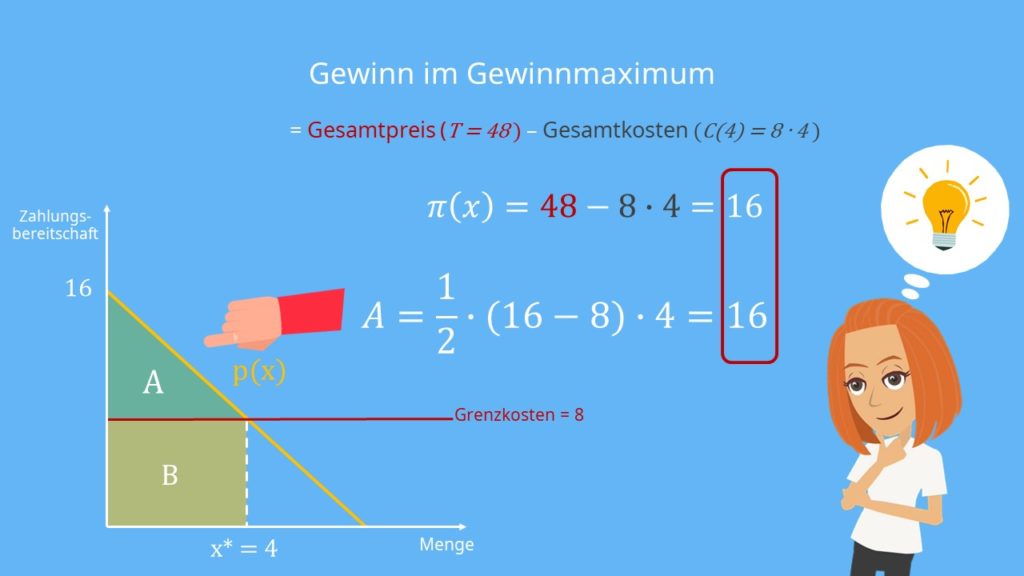
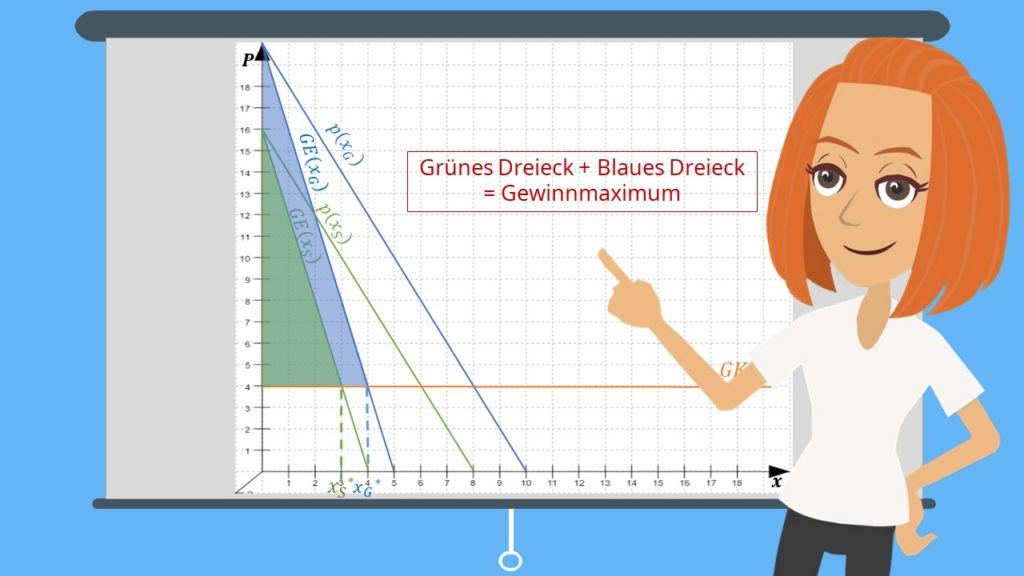
Eine Besonderheit bei der Preisdiskriminierung 1. Grades ist, dass es keinen Stückpreis gibt, da es zu kompliziert wäre für jeden einzelnen Kunden einen Preis zu berechnen. Deswegen legen wir nur einen Gesamtpreis fest. Um zu verstehen wie man diesen ermittelt, schauen wir uns das anhand einer Graphik an:
Der Gesamtpreis ergibt sich aus der Fläche A und der Fläche B. Schauen wir uns zunächst die Größe der Fläche B an. Sie wird von der Nachfragefunktion 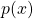 , von der gewinnmaximierenden Menge sowie von der Grenzkostenlinie begrenzt.
, von der gewinnmaximierenden Menge sowie von der Grenzkostenlinie begrenzt.
B stellt somit den gemeinkostendeckenden Betrag dar und gibt die Menge an, die mindestens konsumiert werden muss, damit du keinen Verlust machst. Rechnen wir also die Fläche B aus, um herauszufinden wie viel Limonade wir dafür verkaufen müssen. Die Grenzkosten mal der gewinnmaximierenden Menge ist also 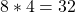
Das Dreieck A liegt über den Grenzkosten.
Preisdiskriminierung: Berechnung des Dreiecks A
Um A zu berechnen, verwendet man einfach die Formel:
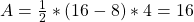
Durch Addition der beiden Flächen A und B erhalten wir nun den Gesamtpreis bei komplettem Konsum. Das ergibt dann einen Wert von 48. Diese Gesamtfläche nennen wir T.
Der Gesamtpreis aller verkauften Flaschen Limonade beträgt also 48 €.
Für den Gewinn im Gewinnmaximum musst Du dann nur noch Deine Gesamtkosten vom Gesamtpreis abziehen:
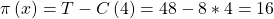
Bestimmt ist dir jetzt aufgefallen, dass der Gewinn deinem Dreieck A entspricht. Du kannst dir also für das Lösen einer solchen Aufgabe merken: Wenn das Dreieck A vollständig über der Grenzkostenlinie liegt, stellt es den Gewinn dar.
Dann musst du nicht mehr beide Flächen addieren, sondern hast so deinen Gewinn schon ermittelt. Dein Gewinnmaximum beträgt also 16 €.
So, wir hoffen du hast die Preisdiskriminierung 1. Grades damit verstanden. Mit der Preisdiskriminierung 2. Grades geht es weiter!
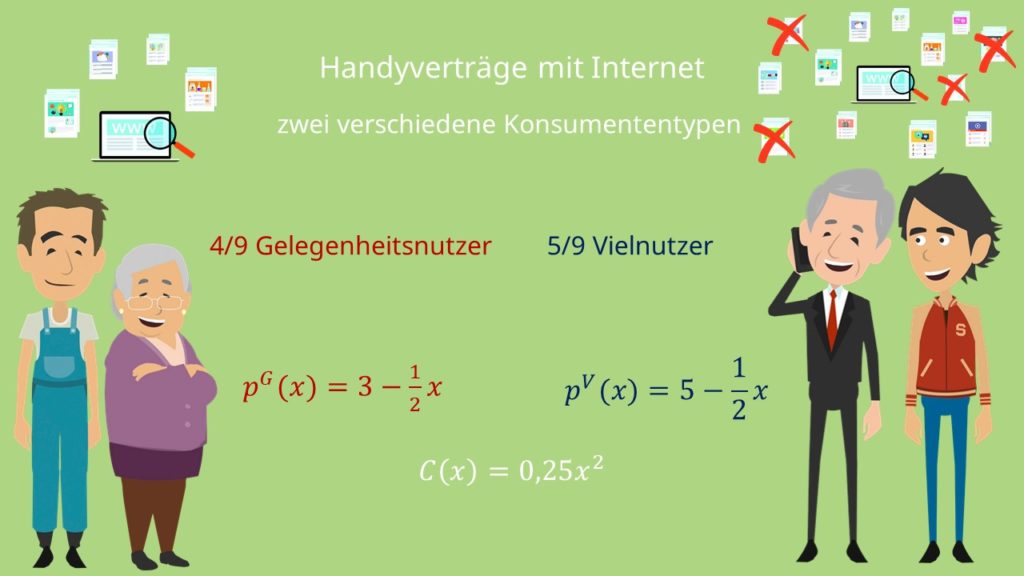
Im Gegensatz zur Preisdiskriminierung 1. Grades kannst du als Unternehmer bei der Preisdiskriminierung 2. Grades nicht mehr zwischen den verschiedenen Kunden unterscheiden. Du musst also einen anderen Weg finden sie zu diskriminieren. Du legst die Preise über die Mengen, die du an einen Kunden verkaufst, fest. Damit du das besser verstehst, nehmen wir als Beispiel Handyverträge mit Internet.
Preisdiskriminierung 2. Grades erklärt
Wir gehen dabei von zwei verschiedenen Konsumententypen aus. 4/9 der Kunden brauchen nur ab und zu Datenvolumen, sie sind also Gelegenheitsnutzer. Die anderen 5/9 sind Vielnutzer, da sie täglich Datenvolumen brauchen. Sie wären aber bereit auf Gigabyte zu verzichten, um Geld zu sparen. Da beide Gruppen ja ein recht unterschiedliches Konsumverhalten haben, hat auch jede von ihnen eine andere Nachfragefunktion. Die Nachfrage der Gelegenheitskonsumenten wird durch die Funktion 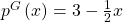 beschrieben. Die der anderen Gruppe durch
beschrieben. Die der anderen Gruppe durch 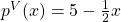 . Beide Gruppen verursachen Kosten von
. Beide Gruppen verursachen Kosten von 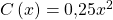 .
.
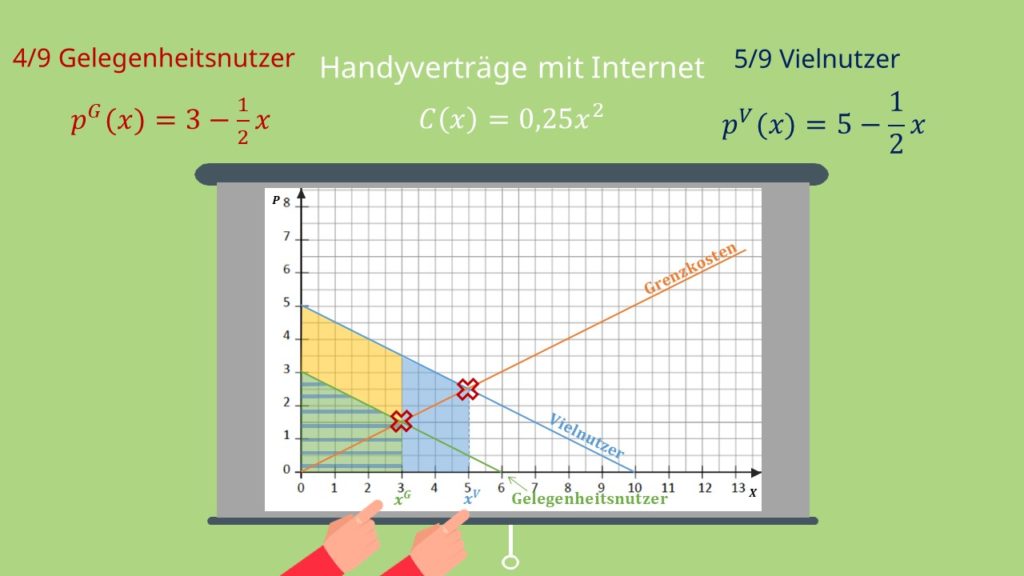
Wir schauen uns das am besten anhand einer Zeichnung an. Die gewinnmaximierende Produktionsmenge bemisst sich wie bei der Preisdiskriminierung 1. Grades am Schnittpunkt der jeweiligen Nachfragefunktion mit den Grenzkosten.
Unterscheidung der Konsumentengruppen
Wenn du die beiden Konsumentengruppen unterscheiden könntest, würdest du dem gelegentlichen Internetnutzer also optimaler Weise 3 Gigabyte und den Vielnutzern, zu einem höheren Preis, 5 Gigabyte anbieten.
Hier jedoch kannst du als Monopolist die verschiedenen Konsumententypen nicht unterscheiden. Du musst dem Kunden also beide Verträge anbieten und ihm die Wahl lassen. Das ist problematisch, da sich die Person mit einer hohen Zahlungsbereitschaft als jemand mit einer geringen Zahlungsbereitschaft ausgeben wird. Sie wird also den günstigeren Vertrag wählen.
Vergleich der Nutzungsarten
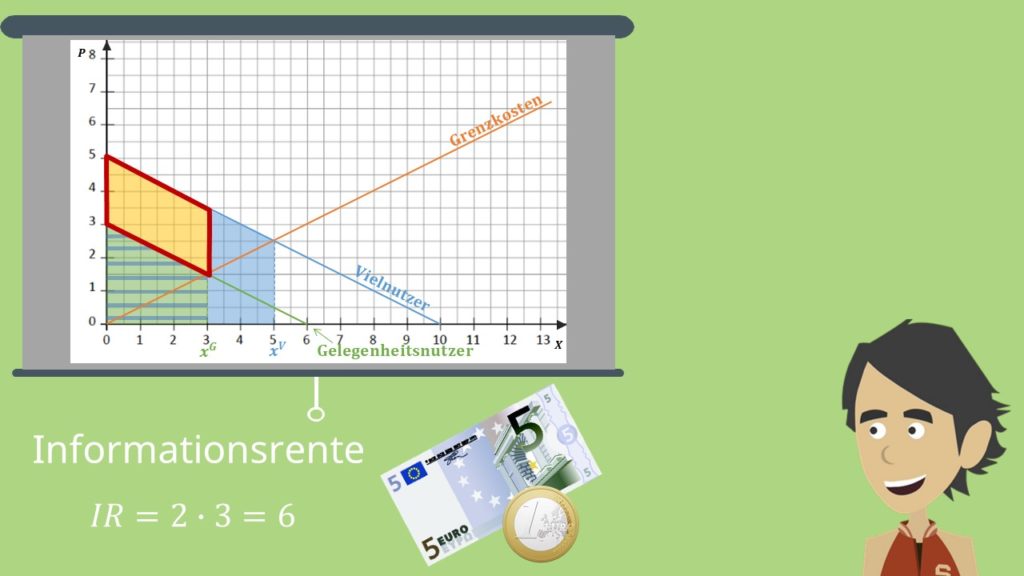
Wieso macht sie das? Das ist ganz einfach. Sie wählt den günstigeren Vertrag, weil sie so einen finanziellen Vorteil hat. Schauen wir in die Zeichnung, sehen wir, dass der Vielnutzer bereit wäre den Betrag der grünen und der gelben Fläche für 3 GB zu zahlen. Da er dafür aber nur die grüne Fläche zahlen muss, wenn er den günstigeren Vertrag wählt, erhält er eine Konsumentenrente, auch Informationsrente genannt.
Die Vielnutzer haben dir gegenüber nämlich einen entscheidenden Informationsvorteil, da sie genau wissen, wie viel Gigabyte sie gerne konsumieren würden. Diese Rente wird durch das gelbe Parallelogramm dargestellt, bemisst sich in Geldeinheiten und lässt sich wie folgt berechnen.
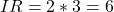
Die Informationsrente beläuft sich auf 6€.
Berechnung der Gesamtzahlung
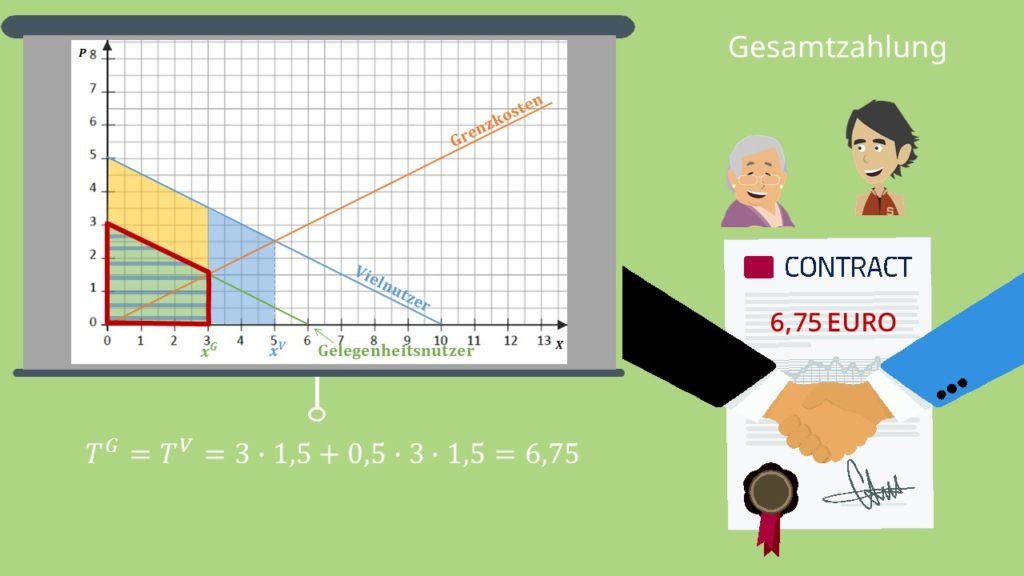
Jetzt kannst du die Gesamtzahlung, also den Preis, pro Vertrag ausrechnen. Wie bei der Preisdiskriminierung 1. Grades bemisst sich diese an der Fläche unterhalb der Nachfragefunktion bis zur gewinnmaximierenden Menge. Da sich auch die Vielnutzer nicht für den Vertrag 2 entscheiden werden, reicht es, wenn wir uns die Gesamtzahlung für den Vertrag 1 anschauen. Das ist die grün-blaue Fläche, die sich so berechnen lässt:
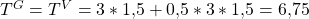
Der Preis für den Vertrag 1 beträgt also 6,75€. Du bekommst also von beiden Gruppen den gleichen Betrag, obwohl sie unterschiedliche Konsumverhalten haben. Das liegt daran, dass wir sie bisher nicht unterscheiden konnten.
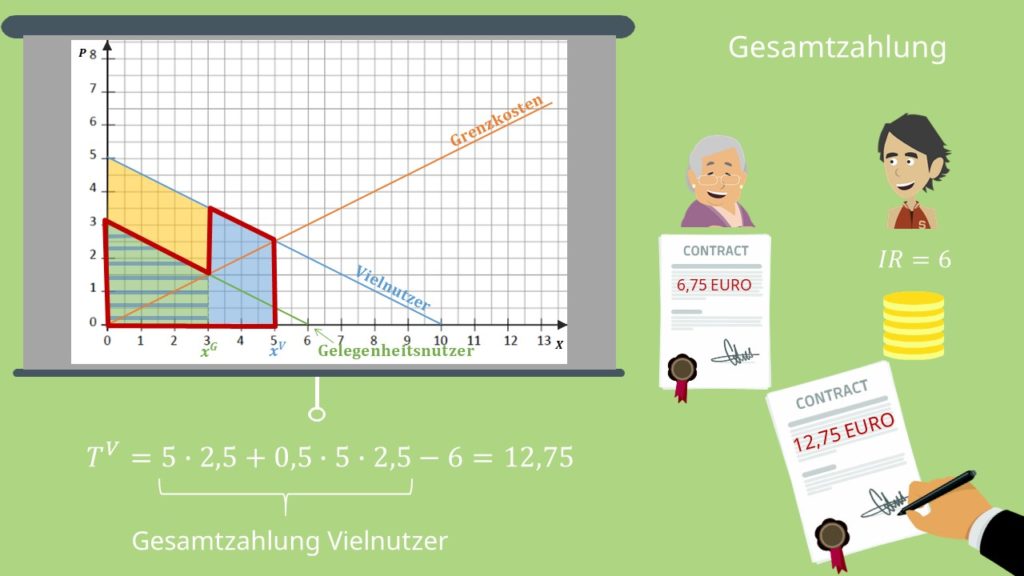
Nun willst Du die Konsumententypen aber unterscheiden können. Da die Vielnutzer nicht auf die Ersparnis der Informationsrente verzichten wollen, müssen wir den Preis des 5 Gigabyte-Vertrags um diesen Betrag senken. Die Vielnutzer werden dann wieder auf die für sie vorgesehene Menge zurückgreifen. Die Gesamtzahlung berechnet sich dann folgendermaßen:
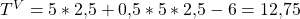
Mit dem Preis von 12,75 € ist der Vertrag für die Vielnutzer also wieder attraktiv. Bei den Gelegenheitsnutzern bleibt hingegen alles gleich.
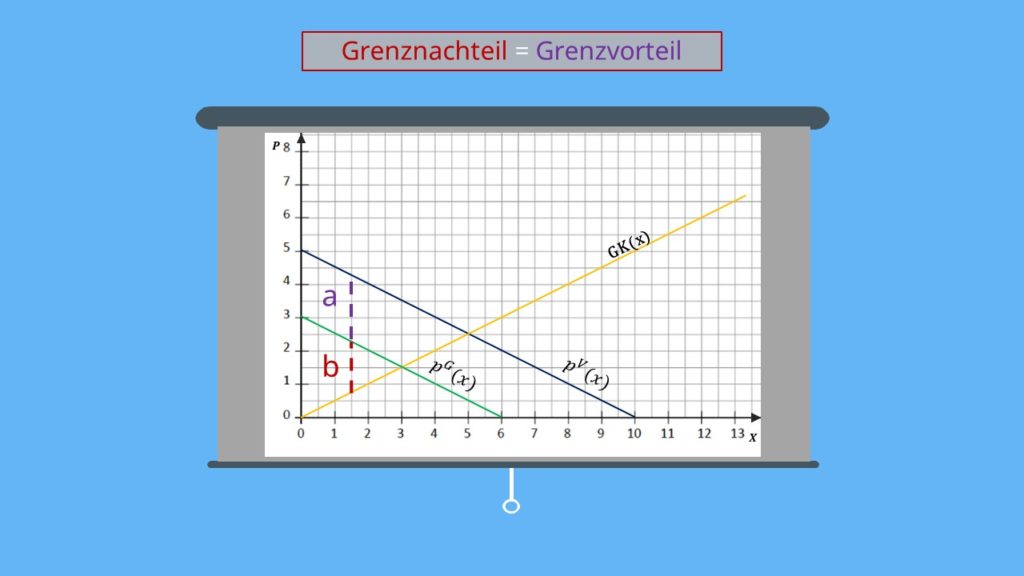
Übersicht über Grenzvorteil und Grenznachteil
Du kannst Deinen Gewinn aber noch weiter erhöhen. Dazu musst Du die Mengen so verändern, dass die täglichen Internetnutzer nicht mehr an der geringeren Menge interessiert sind. Das schaffst du, indem du die Menge der Gelegenheitsnutzer so weit reduzierst, bis der Grenzvorteil dem Grenznachteil entspricht.
Aber was ist das überhaupt? Der Grenznachteil entsteht, weil du der Gruppe der Gelegenheitsnutzer weniger Datenvolumen anbietest. Dir geht also ein Teil Deines Gewinns verloren. Diese Ineffizienz nimmst du als Monopolist in Kauf, da der daraus resultierende Vorteil größer ist. Der Vorteil entsteht daraus, dass sich die Informationsrente verringert und so die Menge der Gelegenheitsnutzer für die Vielnutzer uninteressant wird. Diese bleiben also auf jeden Fall bei ihrem Angebot.
Dies gleicht nicht nur den Nachteil aus, dadurch steigt auch dein Gewinn. Und wenn jetzt gilt, dass der Grenznachteil gleich dem Grenzvorteil ist, dann hast Du Deine Angebotsmengen optimiert. Damit Du noch besser verstehst, was der Grenznachteil ist, holen wir uns wieder die Zeichnung zur Hilfe.
Die Strecke a, der Grenzvorteil, muss der Strecke b, dem Grenznachteil, entsprechen. Als erstes erstellst du dazu für jede der beiden Strecken eine Funktion. Dazu nimmst du für a die Gewichtung der Vielnutzer mal die Nachfragefunktion der Vielnutzer minus die der Gelegenheitsnutzer. Für b erstellst du die Funktion analog: Die Gewichtung der Gelegenheitsnutzer mal die Nachfragefunktion der Gelegenheitsnutzer minus die Grenzkosten. Diese beiden Strecken musst du dann gleichsetzen und deine Werte einsetzen:
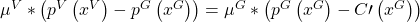
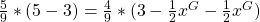
Jetzt stellst Du die Gleichung nach um und schon weißt Du welche Menge Du den Gelegenheitsnutzer anbieten musst:
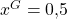
Du bietest also den Gelegenheitskonsumenten nur ein halbes Gigabyte an. Das ist für die Vielnutzer nicht interessant. Sie wählen lieber die für sie vorgesehene Menge, entscheiden sich also für 5 Gigabyte. Für die Gesamtzahlung schauen wir uns das ganze nochmal anhand unserer Graphik an.
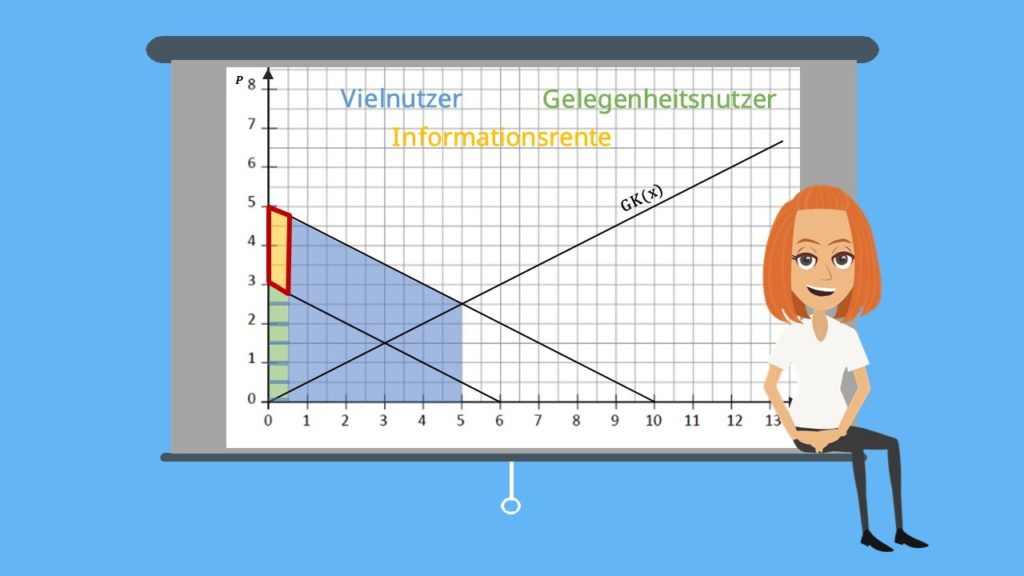
Graphische Veranschaulichung
Die Gesamtzahlung der Vielnutzer umfasst die blaue und die grünblaugestreifte Fläche. Die Gelegenheitskonsumenten zahlen insgesamt nur die grünblaugestreifte Fläche. Das gelbe Parallelogramm ist nach wie vor die Konsumenten- bzw die Informationsrente, für diese muss keiner der beiden Konsumenten aufkommen.
Bei der Preisdiskriminierung 3. Grades unterteilt der Unternehmer seine Kunden in verschiedene Gruppen. Innerhalb der Gruppen macht er aber keinen Unterschied zwischen den Kunden.
Preisdiskriminierung 3. Grades erklärt
Nehmen wir an, Du hast ganz unterschiedliche Kunden, aus jeder sozialen Schicht: also Geringverdiener, Besserverdiener, Studenten, Rentner, Schüler usw. Dann unterteilst Du diese in verschiedene Gruppen, wobei jede ihren eigenen Preis hat. Die Studenten muss z.B. weniger zahlen als die Besserverdiener.
Fackeln wir also nicht lange, sondern fangen wir direkt mit der Berechnung an!
Berechnung der Nachfrage verschiedener Gruppen
Die Nachfrage der Geschäftsleute, die bei Dir Limonade kaufen, wird durch die Funktion 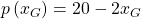 beschrieben. Die der Studenten durch
beschrieben. Die der Studenten durch 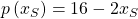 . Beide Kundengruppen verursachen Kosten von
. Beide Kundengruppen verursachen Kosten von 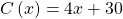 .
.
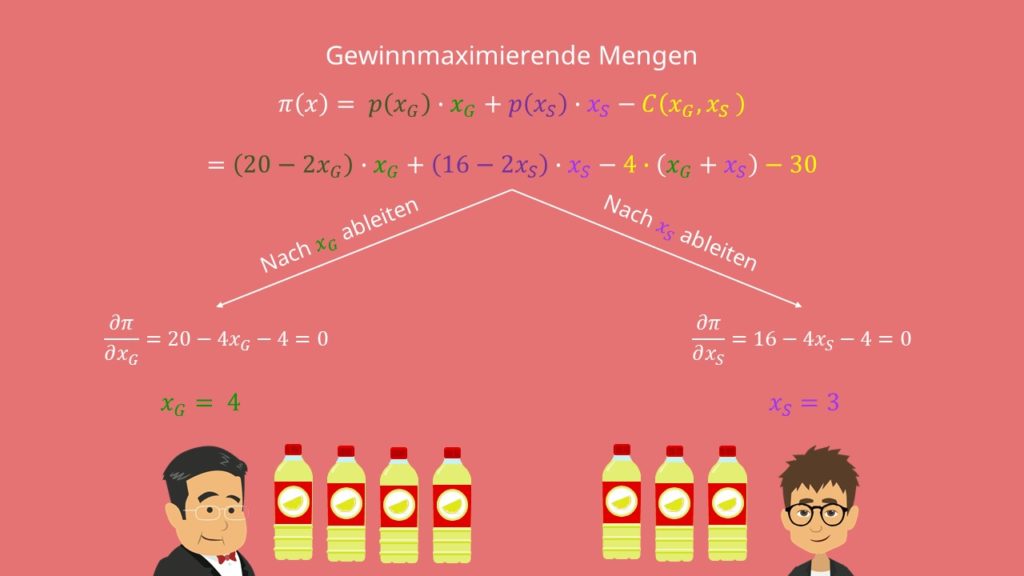
Mit diesen Informationen können wir auch schon mit unserer Berechnung beginnen. Dafür stellen wir zunächst die gemeinsame Gewinngleichung auf:
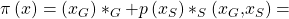
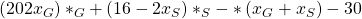
Für die gewinnmaximierenden Mengen musst Du die Gleichung nach beiden Variablen ableiten und dann gleich 0 setzen. Im Prinzip entsprechen einfach nur die Grenzkosten dem Grenzerlös:
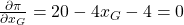
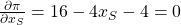
Jetzt musst Du beide Ableitungen nach x umstellen und schon hast Du die gewinnmaximierenden Mengen für beide Konsumentengruppen!
Ergebnis der gewinnmaximierenden Menge
Den Geschäftsleuten solltest Du also 4 Flaschen anbieten und den Studenten 3.
Wenn Du diese Informationen noch in Deine Gewinngleichung einsetzt, weißt Du auch schon wie hoch das Gewinnmaximum Deines Start-ups ist:
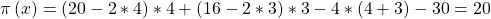
Du kannst also einen maximalen Gewinn von 20 € machen.
Die gewinnmaximierenden Preise
Durch Einsetzen der gewinnmaximierenden Mengen in die Nachfragefunktionen, ergeben sich Deine gewinnmaximierenden Preise:
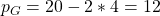
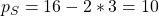
Von den Geschäftsleuten solltest Du also einen Preis von 12€ pro Flasche verlangen. Die Studenten müssen hingegen nur 10€ pro Stück zahlen.
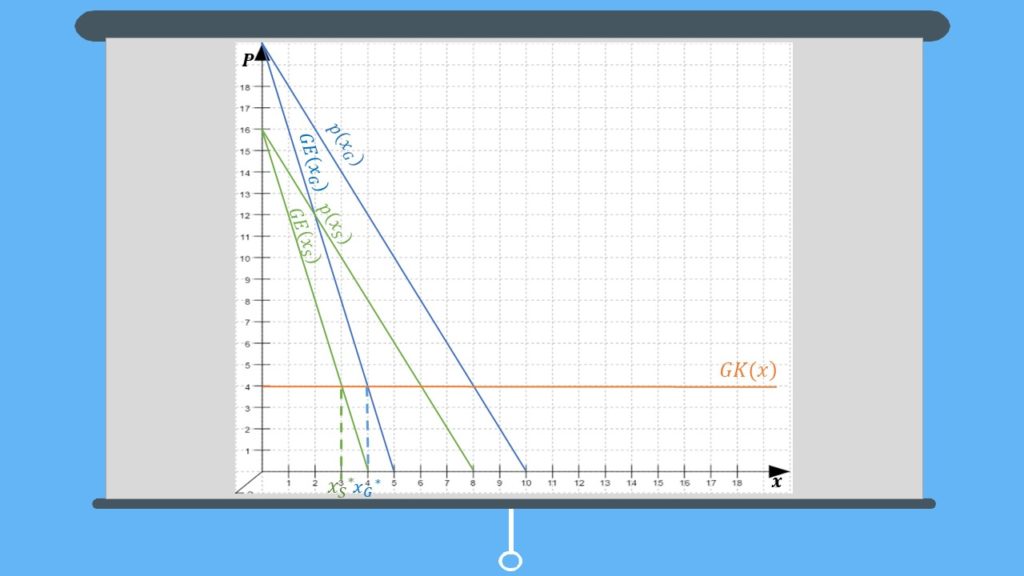
Schauen wir uns das am besten anhand einer Zeichnung an! Meistens kannst Du nämlich schon mithilfe einer einfachen Graphik sehen, was Deine gewinnmaximierenden Mengen sind. Auch das Gewinnmaximum lässt sich in der Regel recht einfach mit einer Zeichnung herausfinden.
Du siehst, im Schnittpunkt der Grenzerlösfunktion mit der Grenzkostenfunktion trifft unsere Regel Grenzkosten = Grenzerlös zu. Die gewinnmaximierenden Mengen liegen also bei 3 und 4 Flaschen.
Berechnung des Gewinns
Dein Gewinn besteht dann nur noch aus den Zahlungen, die über Deine Kosten hinausgehen. Also alles, was über Deinen Grenzkosten und unter der jeweiligen Grenzerlösfunktion liegt. Du müsstest somit nur die Flächen der beiden Dreiecke in Deiner Zeichnung ausrechnen und addieren. So erhältst Du ganz einfach Dein Gewinnmaximum.
Damit haben wir auch die letzte Preisdiskriminierung beendet. Um dir nochmal kurz einen Überblick zu verschaffen, fassen wir die 3. Arten nochmal kurz zusammen.
Zusammenfassung Preisdiskriminierungen
Bei der Preisdiskriminierung 1. Grades kennt der Unternehmer die maximale Zahlungsbereitschaft seiner Konsumenten und kann deshalb für jeden Kunden einen individuellen Preis festlegen. Da hier die komplette Zahlungsbereitschaft abgeschöpft werden kann, spricht man von der perfekten Preisdiskriminierung.
Die Preisdiskriminierung 2. Grades ist es für den Unternehmer nicht mehr möglich zwischen den beiden Unternehmen zu unterscheiden. Vereinfacht geht man von 2 Konsumentengruppe aus, die sich in der Menge die das Unternehmen an die beiden Gruppen verkauft unterscheidet. Wir haben das Beispiel mit den Vielnutzern und den Wenignutzern behandelt.
Bei der Preisdiskriminierung 3. Grades wird meistens zwischen zwei größeren Gruppen unterschieden, die jeweils einen unterschiedlichen Preis für ein Produkt angeboten bekommen. Typische Beispiele sind Rabatte für Rentner oder Studenten im Vergleich zu den Normalpreisen.