Preisdiskriminierung 3. Grades
Bei der Preisdiskriminierung 3. Grades unterteilt der Unternehmer seine Kunden in verschiedene Gruppen. Innerhalb der Gruppen macht er aber keinen Unterschied zwischen den Kunden.
Inhaltsübersicht
Übersicht über die dritte Preisdiskriminierung
Nehmen wir an, Du hast ganz unterschiedliche Kunden, aus jeder sozialen Schicht: also Geringverdiener, Besserverdiener, Studenten, Rentner, Schüler usw. Dann unterteilst Du diese in verschiedene Gruppen, wobei jede ihren eigenen Preis hat. Die Studenten muss z.B. weniger zahlen als die Besserverdiener.
Fackeln wir also nicht lange, sondern fangen wir direkt mit der Berechnung an!
Berechnung der Nachfrage verschiedener Gruppen
Die Nachfrage der Geschäftsleute, die bei Dir Limonade kaufen, wird durch die Funktion 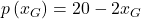 beschrieben. Die der Studenten durch
beschrieben. Die der Studenten durch 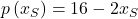 . Beide Kundengruppen verursachen Kosten von
. Beide Kundengruppen verursachen Kosten von 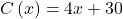 .
.
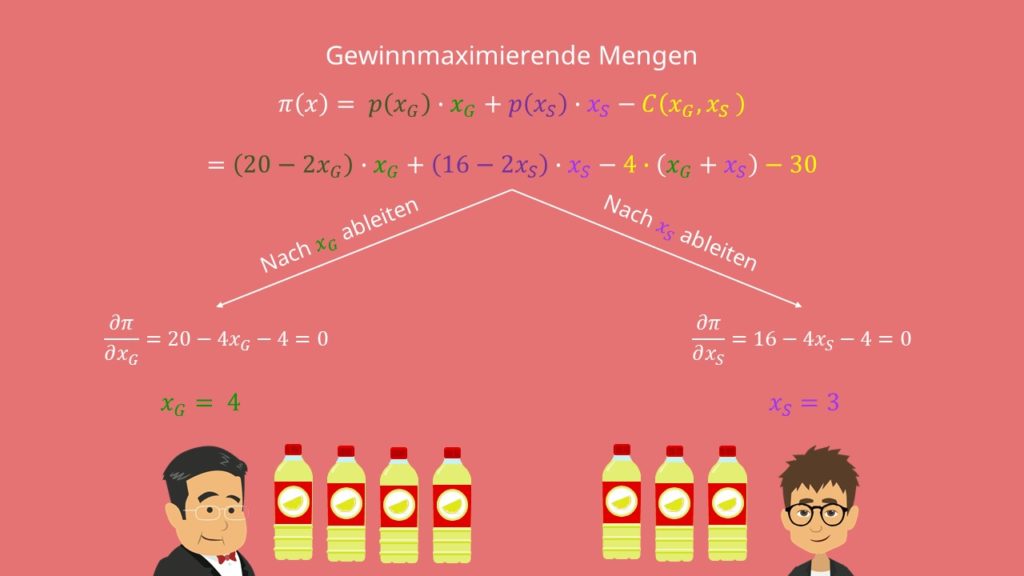
Mit diesen Informationen können wir auch schon mit unserer Berechnung beginnen. Dafür stellen wir zunächst die gemeinsame Gewinngleichung auf:
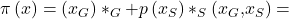
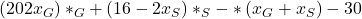
Für die gewinnmaximierenden Mengen musst Du die Gleichung nach beiden Variablen ableiten und dann gleich 0 setzen. Im Prinzip entsprechen einfach nur die Grenzkosten dem Grenzerlös:
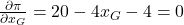
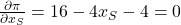
Jetzt musst Du beide Ableitungen nach x umstellen und schon hast Du die gewinnmaximierenden Mengen für beide Konsumentengruppen!
Ergebnis der gewinnmaximierenden Menge
Den Geschäftsleuten solltest Du also 4 Flaschen anbieten und den Studenten 3.
Wenn Du diese Informationen noch in Deine Gewinngleichung einsetzt, weißt Du auch schon wie hoch das Gewinnmaximum Deines Start-ups ist:
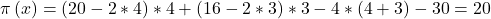
Du kannst also einen maximalen Gewinn von 20 € machen.
Die gewinnmaximierenden Preise
Durch Einsetzen der gewinnmaximierenden Mengen in die Nachfragefunktionen, ergeben sich Deine gewinnmaximierenden Preise:
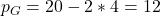
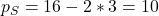
Von den Geschäftsleuten solltest Du also einen Preis von 12€ pro Flasche verlangen. Die Studenten müssen hingegen nur 10€ pro Stück zahlen.
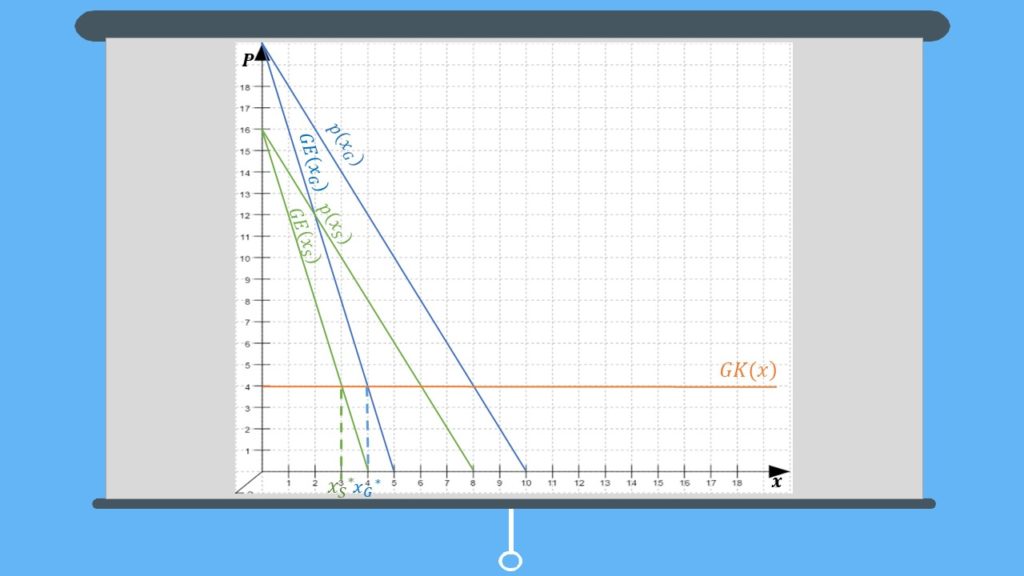
Schauen wir uns das am besten anhand einer Zeichnung an! Meistens kannst Du nämlich schon mithilfe einer einfachen Graphik sehen, was Deine gewinnmaximierenden Mengen sind. Auch das Gewinnmaximum lässt sich in der Regel recht einfach mit einer Zeichnung herausfinden.
Du siehst, im Schnittpunkt der Grenzerlösfunktion mit der Grenzkostenfunktion trifft unsere Regel Grenzkosten = Grenzerlös zu. Die gewinnmaximierenden Mengen liegen also bei 3 und 4 Flaschen.
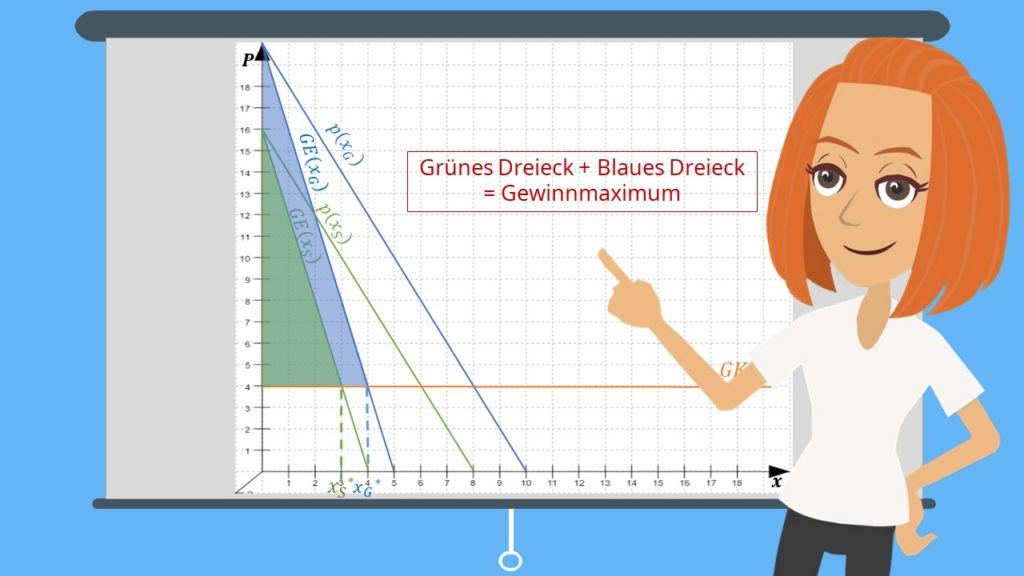
Berechnung des Gewinns
Dein Gewinn besteht dann nur noch aus den Zahlungen, die über Deine Kosten hinausgehen. Also alles, was über Deinen Grenzkosten und unter der jeweiligen Grenzerlösfunktion liegt. Du müsstest somit nur die Flächen der beiden Dreiecke in Deiner Zeichnung ausrechnen und addieren. Damit erhältst Du ganz einfach Dein Gewinnmaximum.
Damit haben wir auch die letzte Preisdiskriminierung beendet. Um dir nochmal kurz einen Überblick zu verschaffen, fassen wir die 3. Arten nochmal kurz zusammen.
Zusammenfassung Preisdiskriminierungen
Bei der Preisdiskriminierung 1. Grades kennt der Unternehmer die maximale Zahlungsbereitschaft seiner Konsumenten und kann deshalb für jeden Kunden einen individuellen Preis festlegen. Da hier die komplette Zahlungsbereitschaft abgeschöpft werden kann, spricht man von der perfekten Preisdiskriminierung.
Die Preisdiskriminierung 2. Grades ist es für den Unternehmer nicht mehr möglich zwischen den beiden Unternehmen zu unterscheiden. Vereinfacht geht man von 2 Konsumentengruppe aus, die sich in der Menge die das Unternehmen an die beiden Gruppen verkauft unterscheidet. Wir haben das Beispiel mit den Vielnutzern und den Wenignutzern behandelt.
Bei der Preisdiskriminierung 3. Grades wird meistens zwischen zwei größeren Gruppen unterschieden, die jeweils einen unterschiedlichen Preis für ein Produkt angeboten bekommen. Typische Beispiele sind Rabatte für Rentner oder Studenten im Vergleich zu den Normalpreisen.