Isoquante
Eine Isoquante stellt die zugehörige Produktionsfunktion graphisch dar und beschreibt das Austauschverhältnis der Produktionsfaktoren dieser Funktion zu einem konstanten Output. In der Mikroökonomie ist sie wichtiger Bestandteil, um das optimale Produktionsniveau von Unternehmen zu berechnen.
Du hast keine Lust einen langen Artikel durchzulesen? Wie man die Isoquante berechnen und zeichnen kann, sowie den Zusammenhang mit der Produktionsfunktion erklären wir dir auch in diesem Video .
Inhaltsübersicht
Isoquante Definition
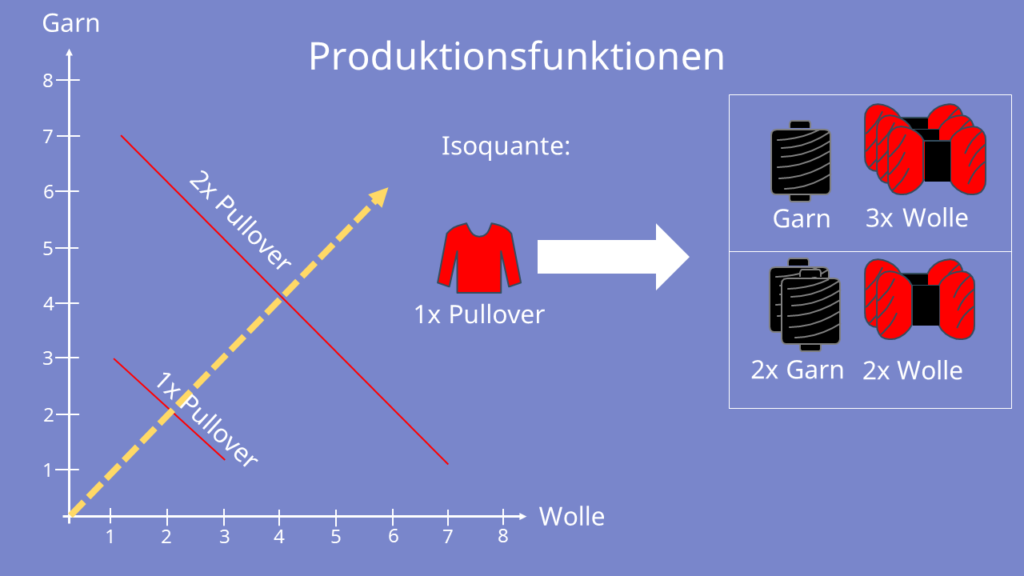
Beginnen wir zunächst mit der allgemeinen Bedeutung von Isoquanten. Diese werden aus der zugehörigen Produktionsfunktion gebildet. Sie wird in der Volkswirtschaft verwendet, um die Beziehung zwischen den Inputs, also den Produktionsfaktoren, und den sich daraus ergebenden Outputs, also den Produkten, darzustellen. Die Produktionsfunktion weist jeder Faktorkombination einen Wert zu, der die Ausbringungsmenge insgesamt widergibt. Wenn Du sie umstellst, hast Du meist auch schon die passende Isoquante. Die Isoquante stellt dar, welche Kombinationen an Inputfaktoren eine bestimmte Outputmenge erzeugt. Auf einer Isoquante bleibt die Ausbringungsmenge also immer gleich. Dabei gilt: je weiter die Isoquante vom Ursprung entfernt ist, desto höher ist die Ausbringungsmenge. Das ist also genau wie bei den Nutzenfunktionen und Indifferenzkurven in der Haushaltstheorie!
Isoquante berechnen
Wie man die Isoquante berechnen kann zeigen wir dir im Folgenden an drei Beispielen. Zunächst wird die Produktionsfunktion umgestellt nach X2 . Anschließend müssen wir mit passenden Güterbündel den Verlauf der Isoquante berechnen. Dabei wird jeder Produktionsfaktormenge zu einem konstanten Outputniveau die jeweilige Menge des anderen Produktionsfaktors bestimmt.
Isoquante zeichnen
Nach der Berechnung lässt sich die entsprechende Isoquante zeichnen, in dem man von den Achsenabschnitten und der Geradensteigung ausgeht. Um einen Achsen Abschnitt zu berechnen, wir der eine Faktor Einsatz gleich null gesetzt. Da aber nur die wenigsten Isoquanten linear sind ist es notwendig, mehrere Faktoreinsatz-Kombinationen zu bestimmen und die entsprechenden Punkte im Koordinatensystem zu markieren. Anschließend musst du die Punkte verbinden und kannst so die Isoquante zeichnen.
Steigung der Isoquante
Die Steigung der Isoquante ist die sogenannte Grenzrate der technischen Substitution: sie gibt an um wie viele Einheiten der 2. Produktionsfaktor erhöht werden muss, wenn zur gleichen Zeit der 1. Produktionsfaktor um eine Einheit reduziert wird und umgekehrt. Dies hat zur Folge, dass bei einem höheren Einsatz beider Produktionsfaktoren auch ein höherer Output erzielt werden kann. Wenn die Isoquante eine negative Steigung aufweist, ist sie auch effizient. Schauen wir uns das Ganze am Beispiel von den gängigsten Isoquanten in der VWL einmal an!
Isoquante Beispiel: Perfekte Substitute
Als erstes nehmen wir uns die Funktionder perfekten Substitute vor. Die wichtigste Eigenschaft der perfekten Substitute ist, dass sie beliebig miteinander vertauschbar sind. Als Beispiel kann man hier als Produktionsfaktoren Erdgas und Diesel nehmen. Beide bringen Dir die gleiche Outputmenge. Die Produktionsfunktion dafür lautet:  . Perfekte Substitute sind also immer additiv miteinander verbunden. Wenn du das Ganze dann nach
. Perfekte Substitute sind also immer additiv miteinander verbunden. Wenn du das Ganze dann nach 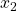 umstellst, hast Du auch schon die passende Isoquante
umstellst, hast Du auch schon die passende Isoquante 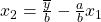 . Das y mit dem Strich darüber bedeutet, dass hier die Outputmenge festgesetzt ist. Die Steigung
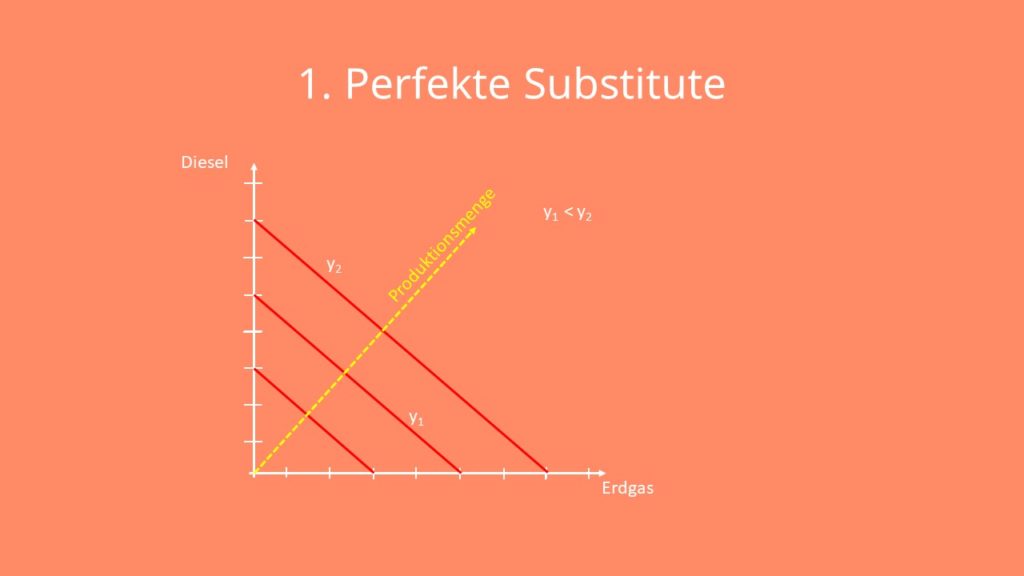
. Das y mit dem Strich darüber bedeutet, dass hier die Outputmenge festgesetzt ist. Die Steigung 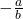 repräsentiert das Austauschverhältnis der beiden Inputfaktoren. Graphisch sieht die Produktionsfunktion dann so aus:
repräsentiert das Austauschverhältnis der beiden Inputfaktoren. Graphisch sieht die Produktionsfunktion dann so aus:
Du siehst bestimmt schon, dass sich die Produktionsmenge auf der Geraden nicht ändert, egal ob du jetzt mehr Erdgas oder mehr Diesel verwendest.
Isoquante Beispiel: Perfekte Komplemente
Weiter geht’s mit den perfekten Komplementen. Wie der Namen eigentlich schon verrät, vervollständigen sich hier beide Inputfaktoren gegenseitig. Das Austauschverhältnis ist also immer konstant. Beim Faktoreinsatz kann das Mischungsverhältnis daher nicht verändert werden, da hier die Substituierbarkeit fehlt. Wenn Du dir das anhand von Einrädern vor Augen führst, verstehst Du die Bedeutung vielleicht schon besser: du brauchst für jedes Einrad einen Rahmen 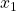 und ein Rad
und ein Rad 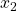 . Sowohl der Rahmen als auch das Rad bringen Dir alleine nichts, da sie sich in ihrem Nutzen ergänzen. Die Produktionsfunktion für perfekte Komplemente ist eine sogenannte Minimum- Funktion und lautet:
. Sowohl der Rahmen als auch das Rad bringen Dir alleine nichts, da sie sich in ihrem Nutzen ergänzen. Die Produktionsfunktion für perfekte Komplemente ist eine sogenannte Minimum- Funktion und lautet: 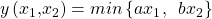 . Sie heißt deswegen Minimum-Funktion, da jedes Komplement natürlich ein Gegenstück braucht. Dir nutzt es also nichts, wenn du nur einen Rahmen, aber dafür 20 Räder hast. Das bedeutet, dass Dein Output dann nur aus einem Einrad besteht. Die restlichen 19 Räder nützen Dir nichts.
. Sie heißt deswegen Minimum-Funktion, da jedes Komplement natürlich ein Gegenstück braucht. Dir nutzt es also nichts, wenn du nur einen Rahmen, aber dafür 20 Räder hast. Das bedeutet, dass Dein Output dann nur aus einem Einrad besteht. Die restlichen 19 Räder nützen Dir nichts.
Da hier die Isoquante nicht explizit darstellbar sind, werden die Mengen der beiden Inputfaktoren stets im Verhältnis 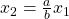 miteinander kombiniert. Das kannst Du Dir aber nicht rechnerisch herleiten, sondern musst es Dir einfach merken. Aber das ist ja zum Glück keine so komplizierte Gleichung!
miteinander kombiniert. Das kannst Du Dir aber nicht rechnerisch herleiten, sondern musst es Dir einfach merken. Aber das ist ja zum Glück keine so komplizierte Gleichung!
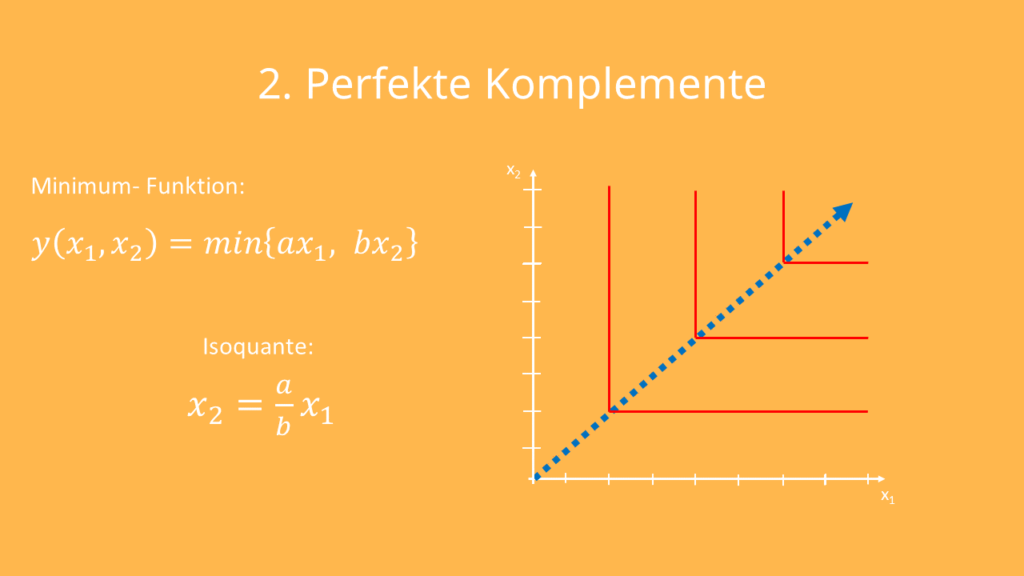
Graphisch kann man das dann so darstellen:
Auf der gepunkteten Linie hast du also von jedem Inputfaktor genau gleich viel. Sobald Du z.B. von Räder 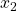 mehr als von Rahmen
mehr als von Rahmen 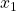 hast, bewegst Du Dich zwar auf der Isoquante nach oben, Du verlässt sie aber nicht. Deine Outputmenge bleibt also gleich.
hast, bewegst Du Dich zwar auf der Isoquante nach oben, Du verlässt sie aber nicht. Deine Outputmenge bleibt also gleich.
Isoquante Beispiel: Imperfekte Substitute
Unser letztes Beispiel ist die graphische Darstellung von imperfekten Substitute. Bei ihnen handelt es sich um Inputfaktoren, die sich in Preis, Qualität oder anderen Merkmalen unterscheiden. Ein gutes Beispiel dafür wäre Leder und Kunstleder. Hier gibt es viele verschiedene Formen, allerdings ist die gängigste Form die Cobb-Douglas-Produktionsfunktion
. Die Cobb-Douglas-Funktion wird durch die Gleichung 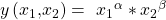 dargestellt. Eine Addition der Faktoren Alpha und Beta lassen Rückschlüsse auf die Skalenerträge
zu. Wenn Du das wiederum nach
dargestellt. Eine Addition der Faktoren Alpha und Beta lassen Rückschlüsse auf die Skalenerträge
zu. Wenn Du das wiederum nach 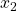 umstellst, hast Du wieder die zugehörige Isoquante
umstellst, hast Du wieder die zugehörige Isoquante 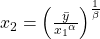 .
.
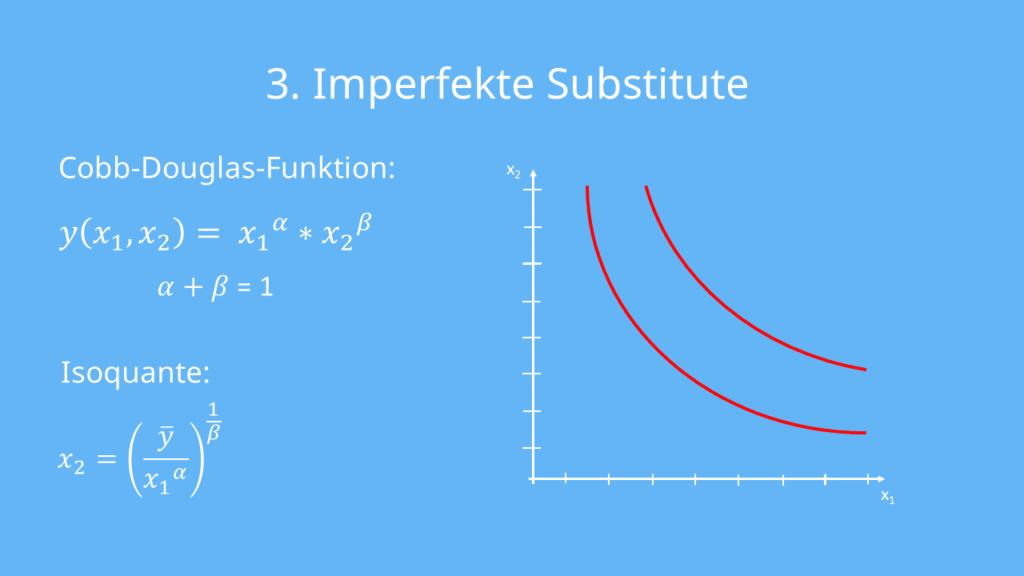
Zur Verdeutlichung haben wir wieder die Produktionsfunktion in einer Grafik:
Du siehst sicher, dass es sich hier um keine lineare Funktion, sondern um eine Exponentialfunktion handelt. Sie ist stets vom Ursprung weggekrümmt also konvex. Mehr von Inputfaktor 1 bringt also eine zusätzliche Outputmenge, aber ersetzt Inputfaktor 2 nicht perfekt.
Zusammenfassung
Damit Du Dir das auch gut merken kannst, haben wir für Dich nochmal die wichtigsten Fakten zusammengefasst: In der Produktionstheorie gibt es drei verschiedene Isoquanten: Erstens, die der perfekten Substitute. Sie repräsentiert Inputfaktoren, die beliebig miteinander vertauscht werden können. Zweitens, die der perfekten Komplemente. Sie ergänzen sich und sind nicht alleine nutzbar. Die dritte und letzte Form ist die der imperfekten Substitute. Bei ihnen handelt es sich um Inputfaktoren, die sich in verschiedenen Merkmalen unterscheiden, aber im Prinzip den gleichen Nutzen haben.