Empirische Verteilungsfunktion
In diesem Artikel erklären wir dir die empirische Verteilungsfunktion anhand eines anschaulichen Beispiels. Du willst das Thema noch schneller verstehen? Dann schau dir unser Video dazu an!
Inhaltsübersicht
Empirische Verteilungsfunktion einfach erklärt
In einer empirischen Verteilungsfunktion kannst du ablesen, wie wahrscheinlich es ist, dass ein Messwert aus deiner Stichprobe höchstens eine bestimmte Größe hat. Anders ausgedrückt zeigt die empirische Verteilungsfunktion also die kumulierten relativen Häufigkeiten
deiner Stichprobe.
In einer empirischen
Verteilungsfunktion könntest du also beispielsweise ablesen, welcher Anteil der Personen in deiner Stichprobe höchstens 35 Jahre alt ist.
Empirische Verteilungsfunktion Formel
Berechnen kannst du einen Wert der empirischen Verteilungsfunktion mit dieser Formel:

 – Verteilungswert des Messwerts
– Verteilungswert des Messwerts 
 – Summiere für alle Werte bis zum Messwert
– Summiere für alle Werte bis zum Messwert 
 – Relative Häufigkeit des Messwerts j
– Relative Häufigkeit des Messwerts j
 – Absolute Häufigkeit des Messwerts j
– Absolute Häufigkeit des Messwerts j
 – Gesamtanzahl der Messwerte in deiner Stichprobe
– Gesamtanzahl der Messwerte in deiner Stichprobe
Wie du bei dieser Formel genau vorgehen musst, sehen wir uns gleich an einem anschaulichen Beispiel an!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Empirische vs. theoretische Verteilungsfunktion
Damit unterscheidet sich die empirische von der theoretischen Verteilungsfunktion
.
Während dir die theoretische Verteilungsfunktion sagt, wie wahrscheinlich es allgemein ist, höchstens eine 5 zu würfeln, sagt dir die empirische Verteilungsfunktion, in welchem Anteil der Fälle bei 20 konkret beobachteten Würfelwürfen höchstens eine 5 gefallen ist.
Empirische Verteilungsfunktion: Beispielrechnung
So, genug Theorie. Sehen wir uns direkt ein Beispiel an:
Stell dir vor, du hast einen Test geschrieben. Die 20 Kursteilnehmenden haben in dem Test folgende Noten erreicht:
Note 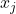
|
1 | 2 | 3 | 4 | 5 | 6 |
Häufigkeit 
|
4 | 5 | 7 | 2 | 1 | 1 |
Vier Personen haben also eine 1 geschrieben, fünf die Note 2 und so weiter und so fort.
Mit der empirischen Verteilungsfunktion kannst du nun berechnen, welcher Anteil des Kurses höchstens eine bestimmte Note erhalten hat. Du könntest also beispielsweise ausrechnen, wie wahrscheinlich es ist, dass eine Person im Kurs die Note 4 oder besser erreicht hat.
Für die Berechnung verwendest du diese Formel:

Die Berechnung ist leichter als du denkst:
-
 ist der Wert, für den du den Wert der Verteilungsfunktion berechnen möchtest. In unserem Beispiel ist das die Note 4, denn du möchtest ja ausrechnen, wie wahrscheinlich es ist, dass eine Person die Note 4 oder besser hatte.
ist der Wert, für den du den Wert der Verteilungsfunktion berechnen möchtest. In unserem Beispiel ist das die Note 4, denn du möchtest ja ausrechnen, wie wahrscheinlich es ist, dass eine Person die Note 4 oder besser hatte. -
 ist die Gesamtzahl deiner Messwerte, in unserem Fall also
ist die Gesamtzahl deiner Messwerte, in unserem Fall also 
-
 ist die Anzahl, wie oft ein bestimmter Messwert vorkommt. Bezogen auf unser Beispiel ist das, wie viele Leute jeweils eine bestimmte Note erhalten haben.
ist die Anzahl, wie oft ein bestimmter Messwert vorkommt. Bezogen auf unser Beispiel ist das, wie viele Leute jeweils eine bestimmte Note erhalten haben.
Diese Werte setzen wir nun in die Formel ein. Für jede Note teilen wir ihre Häufigkeit durch die Anzahl der Kursteilnehmenden. Damit erhältst du die relative Häufigkeit dieser Note. Wir beginnen dabei bei der kleinsten Note und wiederholen die Rechnung bis zu der Note, die uns interessiert. Bezogen auf unser Beispiel berechnen wir die relative Häufigkeit also für die Noten 1,2,3 und 4. Anschließend summierst du die einzelnen relativen Häufigkeiten zu deinem Verteilungswert auf.

Perfekt! In deiner Stichprobe haben also 90% der Personen die Note 4 oder besser erhalten.
Empirische Verteilungsfunktion zeichnen
Jetzt kennst du den Anteil der Personen, der in deiner Stichprobe die Note 4 oder besser erhalten hat. Wenn du die empirische Verteilungsfunktion zeichnen möchtest, musst du den Verteilungswert für jede Notenstufe berechnen. Dabei gehst du genauso vor, wie in unserem Beispiel. Das bedeutet, du berechnest die relativen Häufigkeiten der Notenstufen und summierst sie auf.
Für die Noten 1 bis 3 sieht das so aus:



Richtig gerechnet erhältst du für die verbleibenden Noten folgende Werte:
Note 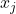 |
1 | 2 | 3 | 4 | 5 | 6 |
Häufigkeit  |
4 | 5 | 7 | 2 | 1 | 1 |
| Relative Häufigkeit h(x_i) | 0,2 | 0,25 | 0,35 | 0,10 | 0,05 | 0,05 |
Verteilungswert  |
0,2 | 0,45 | 0,80 | 0,90 | 0,95 | 1,00 |
Wenn du in die letzte Spalte der Tabelle blickst, siehst du, dass der Verteilungswert für die Note 6 1 lautet. Das ist bei der Verteilungsfunktion immer so. Schließlich ist es ja sicher, dass eine Person eine Note erreicht hat, die entweder die Note 6 oder besser ist, denn andere Noten gibt es ja nicht.
Die Werte aus der Tabelle kannst du nun in ein Koordinatensystem eintragen. Auf der x-Achse stehen die einzelnen Noten von 1 bis 6. Auf der y-Achse wird die Wahrscheinlichkeit eingetragen.
Zeichnest du die Verteilungswerte deiner Noten ein, entsteht eine treppenähnliche Funktion. An ihr kannst du auf einen Blick ablesen, in welchem Anteil der Fälle, höchstens eine bestimmte Note aufgetreten ist.
Weitere Wahrscheinlichkeitsverteilungen
Du möchtest noch mehr über verschiedene theoretische und empirische Wahrscheinlichkeitsverteilungen erfahren? Dann schau doch mal hier vorbei:

