Dichtefunktion
Was ist eine Dichtefunktion? Hier klären wir diese Frage! Dabei unterschieden wir zwischen dem diskreten und dem stetigen Fall. Außerdem wird der Bezug zur Verteilungsfunktion erklärt und mit deren Hilfe Wahrscheinlichkeiten in einem konkreten Beispiel berechnet.
Du lässt dir alles zur Dichtefunktionen lieber kurz und knackig erklären? Unsere Videos Dichtefunktion und Dichtefunktion Übung können das besser als jeder Professor oder Lehrer!
Inhaltsübersicht
Dichtefunktion einfach erklärt
In erster Linie muss man unterscheiden, ob die Dichte von diskreten oder stetigen Variablen betrachtet wird. Bei diskreten Zufallsvariablen spricht man nicht von einer „diskreten Dichtefunktion“, sondern der Wahrscheinlichkeitsfunktion. Diese sagt aber im Grunde genommen dasselbe aus wie eine Dichtefunktion. Der Unterschied liegt darin, dass die Anzahl der Variablen endlich ist und deren Werte genau definiert sind. Jedem dieser Werte kann so eine konkrete Wahrscheinlichkeit zugeordnet werden.
Betrachten wir stetige Variablen , dann ist eine so einfache Zuordnung jedoch nicht möglich, da es sich um unendlich viele mögliche Werte innerhalb eines Intervalls handelt. Aus diesem Grund spricht man bei stetigen Variablen von einer Wahrscheinlichkeitsdichte oder eben der Dichtefunktion. Diese verrät wie dicht die betrachteten Variablen um einen beliebigen Punkt verteilt sind. Je höher die Dichte an dieser Stelle ist, desto höher ist auch die Wahrscheinlichkeit der Realisierung einer Variablen aus diesem Bereich.
Dichte diskrete Variablen
Um zu verstehen was eine Dichtefunktion aussagt, ist es einfacher mit diskreten Zufallsvariable zu beginnen und dann zum stetigen Fall überzugehen. Um die Dichte von diskreten Zufallsvariablen zu bestimmen, betrachten wir zunächst die Zufallsvariable X. Man ordnet nun einfach jedem möglichen Ergebnis x eine Wahrscheinlichkeit zu. Betrachtet man die Wahrscheinlichkeiten bei einem Würfelwurf, so ist jede Augensumme gleich wahrscheinlich. In unserem Beispiel ist die Wahrscheinlichkeit für jedes mögliche Ergebnis 1/6, wir können also schreiben:
 , falls
, falls 
Graphisch dargestellt würde das dann so aussehen:
Aus der graphischen Darstellung kannst du ganz einfach die Wahrscheinlichkeit für jedes Ergebnis deines Zufallsexperiments ablesen.
Diese einfache Veranschaulichung der Dichte verrät dir aber nicht nur die Wahrscheinlichkeiten einzelner Ergebnisse, sondern hilft dir auch bei der Berechnung, mit welcher Wahrscheinlichkeit beispielsweise eine gerade Zahl gewürfelt wird. Dazu summiert man einfach die Werte aller geradzahligen Ergebnisse auf.
P(X∈{2,4,6}) = P(X=2)+P(X=4)+P(X=6)= 0,5
Du solltest dir jedoch merken, dass zwei wichtige Kriterien erfüllt sein müssen, damit von „der Dichte“ im diskreten Fall die Rede sein kann.
- Die Wahrscheinlichkeit für ein mögliches Ergebnis darf niemals kleiner als Null sein. Folglich muss gelten: f(x)≥0 für alle x∈R. In unserem Beispiel handelt es sich um eine diskrete Gleichverteilung, da alle möglichen Ergebnisse gleich wahrscheinlich und alle restlichen reellen Zahlen gleich Null sind. Allgemein ist es aber nicht zwingend notwendig, dass die möglichen Ergebnisse x dieselbe Wahrscheinlichkeit haben.
- Wichtig ist nur, dass die Summe aller einzelnen Wahrscheinlichkeitswerte 1 ergibt. Das ist ja auch nur logisch, da das Ergebnis bei einem Würfel Wurf zwingender Weiße eine Zahl zwischen 1 und 6 ist und man somit zu 100% entweder eine 1,2,3,4,5 oder 6 würfelt. Die Wahrscheinlichkeit eine 7 oder eine andere reelle Zahl zu würfeln ist dabei immer 0.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Stetige Dichtefunktion
Im stetigen Fall sieht das etwas anders aus. Als Dichtefunktion, auch Wahrscheinlichkeitsdichte genannt, werden reelwertige Funktionen bezeichnet, welche die Dichte stetiger Variablen um einen beliebigen Punkt abbilden. Mithilfe der Dichtefunktion kann die Wahrscheinlichkeit ermittelt werden, dass ein Wert realisiert wird, der innerhalb eines vorab definierten Intervalls liegt.
Nehmen wir nun an, du schätzt und misst anschließend die Zeit eines 100 Meter Läufers auf zehn Nachkommastellen genau. Da bei stetigen Zufallsvariablen rein theoretisch alle Zeiten von null bis unendlich möglich sind, ist die Wahrscheinlichkeit, dass du genau richtig schätzt, extrem gering. Nun kannst du aber in der Theorie nicht nur auf zehn, sondern auf unendlich viele Nachkommastellen genau messen. Deshalb ist es unmöglich für ein beliebiges x die exakte Wahrscheinlichkeit zu bestimmen. Der Unterschied zum diskreten Fall ist also, dass man hier keine einzelnen Punkte hat, welche man aufsummieren kann, sondern über unendlich viele Werte ein Integral bildet. Die Wahrscheinlichkeit einzelner Intervalle erhalten wir nun, indem wir die Fläche unter der Dichte berechnen. Wir benötigen also das Integral. Hier wird erneut deutlich, warum wir keine Wahrscheinlichkeiten für exakte Werte bestimmen können. Die Fläche unter einem Punkt ist schließlich immer null.

Die Dichtefunktion vermittelt auch einen guten visuellen Eindruck über die Verteilung einer Zufallsvariablen. Daher bestimmt die zugrundeliegende Verteilung auch den Verlauf der Funktion.
Dichtefunktion Eigenschaften
Die Dichtefunktion stetiger Zufallsvariablen hat drei grundlegende Eigenschaften:
Sie ist erstens immer größer oder gleich null.
 für alle
für alle 
Zweitens ist ihr Integral gleich 1. Aber Vorsicht, die Dichtefunktion kann trotzdem Werte größer eins annehmen, falls die Ausprägungen zum Beispiel zwischen minus eins und eins liegen. Wichtig ist aber, dass die Fläche unter der Funktion, also das Integral immer 1 bleibt.

Und drittens ist die Wahrscheinlichkeit, dass ein ganz bestimmtes Ereignis eintritt gleich null.
 für alle
für alle 
Dichtefunktion bestimmen
Wie du jetzt weißt, sehen die Funktionen unterschiedlich aus, je nachdem ob wir den diskreten oder den stetigen Fall betrachten. Aber auch die Dichtefunktionen stetiger Verteilungen unterscheiden sich in ihrem Verlauf voneinander. Sehen wir uns zur Verdeutlichung einige Dichtefunktion Beispiele an.
Dichtefunktion Normalverteilung
Die Dichtefunktion der Normalverteilung sieht folgendermaßen aus:

Dichtefunktion stetige Gleichverteilung
Im Falle einer stetigen Gleichverteilung sieht die Dichtefunktion auf den ersten Blick etwas komplizierter aus, da diese abschnittsweiße definiert ist. Im Grunde genommen ist diese aber wesentlich einfacher als beispielsweise die der zuvor behandelten Dichtefunktion. Für die stetige Gleichverteilung wird die Dichte folgendermaßen notiert:
Dichtefunktion Exponentialverteilung
Die Dichtefunktion der Exponentialverteiling ist ein fallender Graph für Werte größer 0.
Dichtefunktion Verteilungsfunktion
Um die Wahrscheinlichkeit im stetigen Fall zu berechnen, brauchen wir jedoch nicht nur die Dichte- sondern auch die die Verteilungsfunktion. An der Dichtefunktion lassen sich nämlich keine Wahrscheinlichkeiten ablesen. Integriert man diese jedoch, so erhält man die Verteilungsfunktion und kann mit Hilfe dieser die gesuchten Wahrscheinlichkeiten bestimmen.
Dichtefunktion berechnen
Wir wollen die Frage beantworten, mit welcher Wahrscheinlichkeit ein 100m Läufer diese Strecke in unter 12 Sekunden bewältigt (Beispiel 1). Anschließend wollen wir es noch genauer wissen und stellen uns die Frage: Wie wahrscheinlich ist es, dass er die 100m in 11 – 12 Sekunden zurücklegt (Beispiel 2)?
Dichtefunktion Formel
Gehen wir von einer Normalverteilung aus, so ist die Formel der Dichtefunktion folgende:

Erwartungswert Dichtefunktion
Betrachtet man die beispielsweise die zentralen Maßzahlen der Statistik wie den Erwartungswert, die Varianz oder die Standardabweichung , kann man bereits Aussagen über die Wahrscheinlichkeitsverteilung treffen.
In unserem Fall sind der Erwartungswert und die Varianz gegeben mit  und
und  .
.
Da man sich unter den bloßen Zahlenwerten nur schwer etwas vorstellen kann, hilft es diese graphisch darzustellen.
Dichtefunktion zeichnen
Die Dichtefunktion ist eine visuelle Darstellung der Verteilung deiner Variablen. Sie zeigt also an, in welchem Bereich die Zufallsvariable am stärksten ausgeprägt ist. Zeichnen wir die Dichtefunktion für den 100 Meter Läufer, könnte das zum Beispiel so aussehen:
Man kann ablesen, dass es am wahrscheinlichsten ist, dass ein Läufer die Strecke in rund 14 Sekunden bewältigt. Der Graph verrät uns außerdem, dass es ziemlich unwahrscheinlich ist, dass jemand die Strecke in unter 10 beziehungsweise über 17 Sekunden läuft.
Dichtefunktion Wahrscheinlichkeit berechnen
Wie vorhin bereits erklärt, muss man die Dichtefunktion integrieren, um die Verteilungsfunktion zu erhalten. Nur mit dieser kann man im stetigen Fall die Wahrscheinlichkeit berechnen.
Wir wissen, dass unsere Werte normalverteilt sind, somit rechnen wir mit der Verteilungsfunktion der Normalverteilung. Um die Wahrscheinlichkeit aus der Verteilungstabelle ablesen zu können, müssen wir die Verteilungsfunktion auf die der Standardnormalverteilung transformieren. Dazu setzten wir einfach unsere gegebenen Werte ein uns schlagen den errechneten Wert für in der Verteilungstabelle nach.
Beispiel 1
Kommen wir auf unsere Fragestellung von vorhin zurück: Mit welcher Wahrscheinlichkeit ist der Läufer schneller als 12 Sekunden?
Mathematisch ausgedrückt bedeutet das:

Die Wahrscheinlichkeit für  entspricht dem Funktionswert der Verteilungsfunktion an der Stelle x gleich zwölf.
entspricht dem Funktionswert der Verteilungsfunktion an der Stelle x gleich zwölf.


Unser gesuchter Wert ist 12 und der Erwartungswert ist gegeben mit 14. Da wir nur die Varianz mit 4 gegeben haben, müssen wir noch die Wurzel aus dieser ziehen, um die Standardabweichung zu erhalten.


Lesen wir diesen Wert aus der Verteilungstabelle der standardisierten Normalverteilung ab, so erhalten wir eine Wahrscheinlichkeit von 
| z / Φ(z) | 0 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0 | 0,5 | 0,50399 | 0,50798 | 0,51197 | 0,51595 | 0,51994 | 0,52392 | 0,5279 | 0,53188 | 0,53586 |
| 0,1 | 0,53983 | 0,5438 | 0,54776 | 0,55172 | 0,55567 | 0,55962 | 0,56356 | 0,56749 | 0,57142 | 0,57535 |
| 0,2 | 0,57926 | 0,58317 | 0,58706 | 0,59095 | 0,59483 | 0,59871 | 0,60257 | 0,60642 | 06,1026 | 0,61409 |
| 0,3 | 0,61791 | 0,62172 | 0,62552 | 0,6293 | 0,63307 | 0,63683 | 0,64058 | 0,64431 | 0,64803 | 0,65173 |
| 0,4 | 0,65542 | 0,6591 | 0,66276 | 0,6664 | 0,67003 | 0,67364 | 0,67724 | 0,68082 | 0,68439 | 0,68793 |
| 0,5 | 0,69146 | 0,69497 | 0,69847 | 0,70194 | 0,7054 | 0,70884 | 0,71226 | 0,71566 | 0,71904 | 0,7224 |
| 0,6 | 0,72575 | 0,72907 | 0,73237 | 0,73565 | 0,73891 | 0,74215 | 0,74537 | 0,74857 | 0,75175 | 0,7549 |
| 0,7 | 0,75804 | 0,76115 | 0,76424 | 0,7673 | 0,77035 | 0,77337 | 0,77637 | 0,77935 | 0,7823 | 0,78524 |
| 0,8 | 0,78814 | 0,79103 | 0,79389 | 0,79673 | 0,79955 | 0,80234 | 0,80511 | 0,80785 | 0,81057 | 0,81327 |
| 0,9 | 0,81594 | 0,81859 | 0,82121 | 0,82381 | 0,82639 | 0,82894 | 0,83147 | 0,83398 | 0,83646 | 0,83891 |
| 1 | 0,84134 | 0,84375 | 0,84614 | 0,84849 | 0,85083 | 0,85314 | 0,85543 | 0,85769 | 0,85993 | 0,86214 |
| 1,1 | 0,86433 | 0,8665 | 0,86864 | 0,87076 | 0,87286 | 0,87493 | 0,87698 | 0,879 | 0,881 | 0,88298 |
| 1,2 | 0,88493 | 0,88686 | 0,88877 | 0,89065 | 0,89251 | 0,89435 | 0,89617 | 0,89796 | 0,89973 | 0,90147 |
| 1,3 | 0,9032 | 0,9049 | 0,90658 | 0,90824 | 0,90988 | 0,91149 | 0,91309 | 0,91466 | 0,91621 | 0,91774 |
| 1,4 | 0,91924 | 0,92073 | 0,9222 | 0,92364 | 0,92507 | 0,92647 | 0,92785 | 0,92922 | 0,93056 | 0,93189 |
| 1,5 | 0,93319 | 0,93448 | 0,93574 | 0,93699 | 0,93822 | 0,93943 | 0,94062 | 0,94179 | 0,94295 | 0,94408 |
| 1,6 | 0,9452 | 0,9463 | 0,94738 | 0,94845 | 0,9495 | 0,95053 | 0,95154 | 0,95254 | 0,95352 | 0,95449 |
| 1,7 | 0,95543 | 0,95637 | 0,95728 | 0,95818 | 0,95907 | 0,95994 | 0,9608 | 0,96164 | 0,96246 | 0,96327 |
| 1,8 | 0,96407 | 0,96485 | 0,96562 | 0,96638 | 0,96712 | 0,96784 | 0,96856 | 0,96926 | 0,96995 | 0,97062 |
| 1,9 | 0,97128 | 0,97193 | 0,97257 | 0,9732 | 0,97381 | 0,97441 | 0,975 | 0,97558 | 0,97615 | 0,9767 |
| 2 | 0,97725 | 0,97778 | 0,97831 | 0,97882 | 0,97932 | 0,97982 | 0,9803 | 0,98077 | 0,98124 | 0,98169 |
| 2,1 | 0,98214 | 0,98257 | 0,983 | 0,98341 | 0,98382 | 0,98422 | 0,98461 | 0,985 | 0,98537 | 0,98574 |
| 2,2 | 0,9861 | 0,98645 | 0,98679 | 0,98713 | 0,98745 | 0,98778 | 0,98809 | 0,9884 | 0,9887 | 0,98899 |
| 2,3 | 0,98928 | 0,98956 | 0,98983 | 0,9901 | 0,99036 | 0,99061 | 0,99086 | 0,99111 | 0,99134 | 0,99158 |
| 2,4 | 0,9918 | 0,99202 | 0,99224 | 0,99245 | 0,99266 | 0,99286 | 0,99305 | 0,99324 | 0,99343 | 0,99361 |
| 2,5 | 0,99379 | 0,99396 | 0,99413 | 0,9943 | 0,99446 | 0,99461 | 0,99477 | 0,99492 | 0,99506 | 0,9952 |
| 2,6 | 0,99534 | 0,99547 | 0,9956 | 0,99573 | 0,99585 | 0,99598 | 0,99609 | 0,99621 | 0,99632 | 0,99643 |
| 2,7 | 0,99653 | 0,99664 | 0,99674 | 0,99683 | 0,99693 | 0,99702 | 0,99711 | 0,9972 | 0,99728 | 0,99736 |
| 2,8 | 0,99744 | 0,99752 | 0,9976 | 0,99767 | 0,99774 | 0,99781 | 0,99788 | 0,99795 | 0,99801 | 0,99807 |
| 2,9 | 0,99813 | 0,99819 | 0,99825 | 0,99831 | 0,99836 | 0,99841 | 0,99846 | 0,99851 | 0,99856 | 0,99861 |
| 3 | 0,99865 | 0,99869 | 0,99874 | 0,99878 | 0,99882 | 0,99886 | 0,99889 | 0,99893 | 0,99896 | 0,999 |
| 3,1 | 0,99903 | 0,99906 | 0,9991 | 0,99913 | 0,99916 | 0,99918 | 0,99921 | 0,99924 | 0,99926 | 0,99929 |
| 3,2 | 0,99931 | 0,99934 | 0,99936 | 0,99938 | 0,9994 | 0,99942 | 0,99944 | 0,99946 | 0,99948 | 0,9995 |
| 3,3 | 0,99952 | 0,99953 | 0,99955 | 0,99957 | 0,99958 | 0,9996 | 0,99961 | 0,99962 | 0,99964 | 0,99965 |
| 3,4 | 0,99966 | 0,99968 | 0,99969 | 0,9997 | 0,99971 | 0,99972 | 0,99973 | 0,99974 | 0,99975 | 0,99976 |
| 3,5 | 0,99977 | 0,99978 | 0,99978 | 0,99979 | 0,9998 | 0,99981 | 0,99981 | 0,99982 | 0,99983 | 0,99983 |
| 3,6 | 0,99984 | 0,99985 | 0,99985 | 0,99986 | 0,99986 | 0,99987 | 0,99987 | 0,99988 | 0,99988 | 0,99989 |
| 3,7 | 0,99989 | 0,9999 | 0,9999 | 0,9999 | 0,99991 | 0,99991 | 0,99992 | 0,99992 | 0,99992 | 0,99992 |
| 3,8 | 0,99993 | 0,99993 | 0,99993 | 0,99994 | 0,99994 | 0,99994 | 0,99994 | 0,99995 | 0,99995 | 0,99995 |
| 3,9 | 0,99995 | 0,99995 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99997 | 0,99997 |
| 4 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99998 | 0,99998 | 0,99998 | 0,99998 |
Somit ist der Läufer mit einer Wahrscheinlichkeit von rund 16% schneller als 12 Sekunden.
Beispiel 2
Soweit ist das ja alles sehr einfach, oder? Aber wie berechnet man nun die Wahrscheinlichkeit, dass der Läufer zum Beispiel zwischen 11 und 12 Sekunden braucht?

Auch das ist keine Hexerei. Du ziehst einfach den Funktionswert der Verteilungsfunktion an der Stelle x gleich elf von dem Funktionswert an der Stelle x gleich zwölf ab.
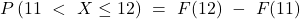
Das wird besonders deutlich, wenn du dir das Ganze graphisch unter der Dichtefunktion vorstellst.
Setzten wir unsere Werte ein, so erhalten wir:





Lesen wir nun die Werte aus der Tabelle der Standardnormalverteilung ab:
| z / Φ(z) | 0 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0 | 0,5 | 0,50399 | 0,50798 | 0,51197 | 0,51595 | 0,51994 | 0,52392 | 0,5279 | 0,53188 | 0,53586 |
| 0,1 | 0,53983 | 0,5438 | 0,54776 | 0,55172 | 0,55567 | 0,55962 | 0,56356 | 0,56749 | 0,57142 | 0,57535 |
| 0,2 | 0,57926 | 0,58317 | 0,58706 | 0,59095 | 0,59483 | 0,59871 | 0,60257 | 0,60642 | 06,1026 | 0,61409 |
| 0,3 | 0,61791 | 0,62172 | 0,62552 | 0,6293 | 0,63307 | 0,63683 | 0,64058 | 0,64431 | 0,64803 | 0,65173 |
| 0,4 | 0,65542 | 0,6591 | 0,66276 | 0,6664 | 0,67003 | 0,67364 | 0,67724 | 0,68082 | 0,68439 | 0,68793 |
| 0,5 | 0,69146 | 0,69497 | 0,69847 | 0,70194 | 0,7054 | 0,70884 | 0,71226 | 0,71566 | 0,71904 | 0,7224 |
| 0,6 | 0,72575 | 0,72907 | 0,73237 | 0,73565 | 0,73891 | 0,74215 | 0,74537 | 0,74857 | 0,75175 | 0,7549 |
| 0,7 | 0,75804 | 0,76115 | 0,76424 | 0,7673 | 0,77035 | 0,77337 | 0,77637 | 0,77935 | 0,7823 | 0,78524 |
| 0,8 | 0,78814 | 0,79103 | 0,79389 | 0,79673 | 0,79955 | 0,80234 | 0,80511 | 0,80785 | 0,81057 | 0,81327 |
| 0,9 | 0,81594 | 0,81859 | 0,82121 | 0,82381 | 0,82639 | 0,82894 | 0,83147 | 0,83398 | 0,83646 | 0,83891 |
| 1 | 0,84134 | 0,84375 | 0,84614 | 0,84849 | 0,85083 | 0,85314 | 0,85543 | 0,85769 | 0,85993 | 0,86214 |
| 1,1 | 0,86433 | 0,8665 | 0,86864 | 0,87076 | 0,87286 | 0,87493 | 0,87698 | 0,879 | 0,881 | 0,88298 |
| 1,2 | 0,88493 | 0,88686 | 0,88877 | 0,89065 | 0,89251 | 0,89435 | 0,89617 | 0,89796 | 0,89973 | 0,90147 |
| 1,3 | 0,9032 | 0,9049 | 0,90658 | 0,90824 | 0,90988 | 0,91149 | 0,91309 | 0,91466 | 0,91621 | 0,91774 |
| 1,4 | 0,91924 | 0,92073 | 0,9222 | 0,92364 | 0,92507 | 0,92647 | 0,92785 | 0,92922 | 0,93056 | 0,93189 |
| 1,5 | 0,93319 | 0,93448 | 0,93574 | 0,93699 | 0,93822 | 0,93943 | 0,94062 | 0,94179 | 0,94295 | 0,94408 |
| 1,6 | 0,9452 | 0,9463 | 0,94738 | 0,94845 | 0,9495 | 0,95053 | 0,95154 | 0,95254 | 0,95352 | 0,95449 |
| 1,7 | 0,95543 | 0,95637 | 0,95728 | 0,95818 | 0,95907 | 0,95994 | 0,9608 | 0,96164 | 0,96246 | 0,96327 |
| 1,8 | 0,96407 | 0,96485 | 0,96562 | 0,96638 | 0,96712 | 0,96784 | 0,96856 | 0,96926 | 0,96995 | 0,97062 |
| 1,9 | 0,97128 | 0,97193 | 0,97257 | 0,9732 | 0,97381 | 0,97441 | 0,975 | 0,97558 | 0,97615 | 0,9767 |
| 2 | 0,97725 | 0,97778 | 0,97831 | 0,97882 | 0,97932 | 0,97982 | 0,9803 | 0,98077 | 0,98124 | 0,98169 |
| 2,1 | 0,98214 | 0,98257 | 0,983 | 0,98341 | 0,98382 | 0,98422 | 0,98461 | 0,985 | 0,98537 | 0,98574 |
| 2,2 | 0,9861 | 0,98645 | 0,98679 | 0,98713 | 0,98745 | 0,98778 | 0,98809 | 0,9884 | 0,9887 | 0,98899 |
| 2,3 | 0,98928 | 0,98956 | 0,98983 | 0,9901 | 0,99036 | 0,99061 | 0,99086 | 0,99111 | 0,99134 | 0,99158 |
| 2,4 | 0,9918 | 0,99202 | 0,99224 | 0,99245 | 0,99266 | 0,99286 | 0,99305 | 0,99324 | 0,99343 | 0,99361 |
| 2,5 | 0,99379 | 0,99396 | 0,99413 | 0,9943 | 0,99446 | 0,99461 | 0,99477 | 0,99492 | 0,99506 | 0,9952 |
| 2,6 | 0,99534 | 0,99547 | 0,9956 | 0,99573 | 0,99585 | 0,99598 | 0,99609 | 0,99621 | 0,99632 | 0,99643 |
| 2,7 | 0,99653 | 0,99664 | 0,99674 | 0,99683 | 0,99693 | 0,99702 | 0,99711 | 0,9972 | 0,99728 | 0,99736 |
| 2,8 | 0,99744 | 0,99752 | 0,9976 | 0,99767 | 0,99774 | 0,99781 | 0,99788 | 0,99795 | 0,99801 | 0,99807 |
| 2,9 | 0,99813 | 0,99819 | 0,99825 | 0,99831 | 0,99836 | 0,99841 | 0,99846 | 0,99851 | 0,99856 | 0,99861 |
| 3 | 0,99865 | 0,99869 | 0,99874 | 0,99878 | 0,99882 | 0,99886 | 0,99889 | 0,99893 | 0,99896 | 0,999 |
| 3,1 | 0,99903 | 0,99906 | 0,9991 | 0,99913 | 0,99916 | 0,99918 | 0,99921 | 0,99924 | 0,99926 | 0,99929 |
| 3,2 | 0,99931 | 0,99934 | 0,99936 | 0,99938 | 0,9994 | 0,99942 | 0,99944 | 0,99946 | 0,99948 | 0,9995 |
| 3,3 | 0,99952 | 0,99953 | 0,99955 | 0,99957 | 0,99958 | 0,9996 | 0,99961 | 0,99962 | 0,99964 | 0,99965 |
| 3,4 | 0,99966 | 0,99968 | 0,99969 | 0,9997 | 0,99971 | 0,99972 | 0,99973 | 0,99974 | 0,99975 | 0,99976 |
| 3,5 | 0,99977 | 0,99978 | 0,99978 | 0,99979 | 0,9998 | 0,99981 | 0,99981 | 0,99982 | 0,99983 | 0,99983 |
| 3,6 | 0,99984 | 0,99985 | 0,99985 | 0,99986 | 0,99986 | 0,99987 | 0,99987 | 0,99988 | 0,99988 | 0,99989 |
| 3,7 | 0,99989 | 0,9999 | 0,9999 | 0,9999 | 0,99991 | 0,99991 | 0,99992 | 0,99992 | 0,99992 | 0,99992 |
| 3,8 | 0,99993 | 0,99993 | 0,99993 | 0,99994 | 0,99994 | 0,99994 | 0,99994 | 0,99995 | 0,99995 | 0,99995 |
| 3,9 | 0,99995 | 0,99995 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99997 | 0,99997 |
| 4 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99998 | 0,99998 | 0,99998 | 0,99998 |

Somit wissen wir, dass der Läufer die Strecke von 100m mit einer Wahrscheinlichkeit von rund 9,2% in 11 bis 12 Sekunden bewältigt.







