Verteilungsfunktion: stetig
Wir zeigen dir hier wie man eine Verteilungsfunktion bestimmen und im stetigen Fall mit dieser Rechnen kann.
Unsere Videos zu den Themen diskrete Verteilungsfunktion und zu stetige Verteilungsfunktion erklären dir alles zu Verteilungsfunktionen verständlich und in Kürze, sodass du die eingesparte Zeit auf andere Aktivitäten verteilen kannst.
Inhaltsübersicht
Verteilungsfunktion einfach erklärt
Die Verteilungsfunktion gibt an, mit welcher Wahrscheinlichkeit das Ergebnis des Zufallsexperiments kleiner oder gleich eines bestimmten Wertes ist. Dafür werden alle Ergebnisse bis zu diesem Wert aggregiert, also „aufaddiert“. Deshalb spricht man auch oft von einer kumulativen Verteilungsfunktion. Allgemein wird die Verteilungsfunktion mathematisch mit P(X≤x) dargestellt und mit F(x) abgekürzt. Klein x ist dabei der Wert, bis zu dem aggregiert wird. Um eine konkrete Verteilungsfunktion bestimmen zu können, muss man als erstes klären, ob es sich um diskrete Zufallsvariablen oder stetige Zufallsvariablen handelt. Dazu betrachtet man die möglichen Ergebnisse und deren Dichte.
Während eine Verteilungsfunktion die Wahrscheinlichkeitsverteilung stetiger Zufallsvariablen vollständig beschreiben kann, gibt es auch sogenannte Maßzahlen, die eine lediglich punktuelle Betrachtung ermöglichen. Zu diesen Maßzahlen zählt beispielsweise der oft in der Statistik verwendete Erwartungswert .
Stetige Verteilungsfunktion
Hat man es mit stetigen Zufallsvariablen zu tun, so kann zur Berechnung von Wahrscheinlichkeiten nur die entsprechende Verteilungsfunktion verwendet werden, welche man durch Integration der Dichtefunktion erhält.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Stetige Verteilungsfunktion zeichnen
Zur Veranschaulichung wird im Folgenden eine einfache Verteilungsfunktion gezeichnet. Es ist dieser Graph einer Dichtefunktion gegeben. Die Wahrscheinlichkeit  entspricht der blau markierten Fläche.
entspricht der blau markierten Fläche.
Man bildet also das Integral von  bis 4 und erhält so den Funktionswert der Verteilungsfunktion an der Stelle
bis 4 und erhält so den Funktionswert der Verteilungsfunktion an der Stelle  . Analog kann so jeder einzelne Punkt der kumulativen Verteilungsfunktion bestimmt werden.
. Analog kann so jeder einzelne Punkt der kumulativen Verteilungsfunktion bestimmt werden.
Stetige Verteilungsfunktion berechnen
Allgemein gilt für Berechnungen mit stetigen Verteilungen, dass es keine Rolle spielt ob die Intervallgrenzen zum Intervall gehören oder nicht. Dies wird anhand folgender Rechenregeln deutlich, welche du auf jeden Fall im Kopf behalten solltest.
1, Es gilt  . Das liegt daran, dass ein einzelner Wert x die Wahrscheinlichkeit von 0 hat.
. Das liegt daran, dass ein einzelner Wert x die Wahrscheinlichkeit von 0 hat.
2, Außerdem gilt für die Wahrscheinlichkeit eines Intervalls  Diese Bedingung musst du beachten, wenn du Wahrscheinlichkeiten berechnen möchtest, welche zwischen zwei Werten liegen.
Diese Bedingung musst du beachten, wenn du Wahrscheinlichkeiten berechnen möchtest, welche zwischen zwei Werten liegen.
3, Man betrachtet das Gegenereignis, wenn man die Wahrscheinlichkeit für > Aussagen berechnen möchte: 
Für unser Rechenbeispiel ist folgende stetige Verteilungsfunktion gegeben:

Gefragt ist nach der Wahrscheinlichkeit, dass X kleiner als 3,5 ist. Um das Ergebnis zu erhalten, setzten wir die Intervallgrenze, also den konkreten Wert in die Verteilungsfunktion ein.



Nun ist die Frage, mit welcher Wahrscheinlichkeit das X zwischen 2,2 und 2,8 liegt. Hier kommt die zweite Rechenregel zur Anwendung. Wir rechnen also:

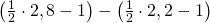


Als letztes wollen wir die Wahrscheinlichkeit berechnen, dass X größer als 3,6 ist. Hier greift die 3.Rechenregel. Wir rechnen also mit der Gegenwahrscheinlichkeit:





Ein weiteres Rechenbeispiel findest du auch in unserem Video zur Dichtefunktion . Dort erfährst du auch, wie du die gesuchten Wahrscheinlichkeiten nicht nur berechnen, sondern die gesuchten Werte aus der Verteilungstabelle ablesen kannst.
Verteilungsfunktion Beispiel: stetig
Wie bereits erwähnt kann zu jeder Wahrscheinlichkeitsverteilung, egal ob diskret oder stetig, eine Verteilungsfunktion gebildet werden. Im Folgenden wird eine Übersicht über die wichtigsten stetigen Verteilungen mit den dazugehörigen Verteilunsfunktionen gegeben.
Verteilungsfunktion Normalverteilung
Die Formel der Verteilungsfunktion der Normalverteilung sieht sehr ungemütlich aus.
Sie summiert alle einzelnen Werte von  bis zum Wert
bis zum Wert  auf und bildet das Integral über die Werte der Dichtefunktion.
auf und bildet das Integral über die Werte der Dichtefunktion.
Aber keine Sorge, da wir es in der Realität mich unendlich vielen stetigen Werten zu tun haben, benutzt man die Verteilungstabelle der Standardnormalverteilung, aus welcher man die gesuchten Wahrscheinlichkeiten nur noch ablesen musst.
Stetige Gleichverteilung Verteilungsfunktion
Die Verteilungsfunktion der stetigen Gleichverteilung gibt man ebenso wie im diskreten Fall aufgeteilt in Abschnitte an:
Verteilungsfunktion Exponentialverteilung
Ebenso wie bei der Dichtefunktion der Exponentailverteilung lassen sich Wahrscheinlichkeiten mit der kumulierten Verteilungsfunktion in diesem Zusammenhang nur für Werte aus dem positiven Bereich berechnen.



