Video

Quiz

Hier geht's zum Video „Bedingte Wahrscheinlichkeit“

Vierfeldertafel

Wichtige Inhalte in diesem Video

Vierfeldertafel einfach erklärt

Vierfeldertafel Aufgaben

Bedingte Wahrscheinlichkeit Vierfeldertafel

Du möchtest wissen, wie du richtig mit einer Vierfeldertafel arbeitest? In unserem Beitrag und Video erfährst du alles, was du wissen musst!

Inhaltsübersicht

Vierfeldertafel einfach erklärt

im Videozur Stelle im Video springen

Neben einem Baumdiagramm kann dir die Vierfeldertafel beim Rechnen mit Wahrscheinlichkeiten helfen. Die Buchstaben A und B bezeichnen dabei zwei Ereignisse. $\overline{A}$ und $\overline{B}$ sind ihre Gegenereignisse.

In der ersten Zeile stehen die Symbole für die Ereignisse A und $\overline{A}$ . In der ersten Spalte stehen wiederum die Ereignisse B und $\overline{B}$ . In die mittleren Kästchen schreibst du die Schnittmenge der Ereignisse:

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} \renewcommand{\arraystretch}{2} & A & \overline{A} & \\ \hline B & $\textcolor{olive}{P (A\cap B)}$&$\textcolor{olive}{P(\overline{A}\cap B)}$&\\ \hline \overline{B}& $\textcolor{olive}{P (A\cap \overline{B})}$&$\textcolor{olive}{P(\overline{A}\cap \overline{B})}$& \\ \hline &&&& \end{tabular}$

$\textcolor{olive}{P (A\cap B)}$ = Wahrscheinlichkeit, dass A und B gleichzeitig eintreten
$\textcolor{olive}{P(\overline{A}\cap B)}$ = Wahrscheinlichkeit, dass A nicht eintritt, aber B schon
$\textcolor{olive}{P (A\cap \overline{B})}$ = Wahrscheinlichkeit, dass A eintritt, aber B nicht
$\textcolor{olive}{P(\overline{A}\cap \overline{B})}$ = Wahrscheinlichkeit, dass weder A noch B eintreten

Die vollständig ausgefüllte Vierfeldertafel sieht so aus:

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} \renewcommand{\arraystretch}{2} & A & \overline{A} & \\ \hline B & $\textcolor{olive}{P (A\cap B)}$&$\textcolor{olive}{P(\overline{A}\cap B)}$&$\textcolor{blue}{P (B)}$\\ \hline \overline{B}& $\textcolor{olive}{P (A\cap \overline{B})}$&$\textcolor{olive}{P(\overline{A}\cap \overline{B})}$&$\textcolor{blue}{P(\overline{B})}}$ \\ \hline &$\textcolor{blue}{P(A)}$&$\textcolor{blue}{P(\overline{A})}$&$\textcolor{orange}{100\%}$& \end{tabular}$

In der rechten Spalte siehst du die einzelnen Wahrscheinlichkeiten von Ereignis B. Um die zu bekommen, rechnest du einfach die nebeneinanderstehenden Wahrscheinlichkeiten zusammen:

Zeile : $\textcolor{olive}{P (A\cap B)}+ \textcolor{olive}{P(\overline{A}\cap B)} = \textcolor{blue}{P (B)}$
Zeile $\overline{B}$ : $\textcolor{olive}{P (A\cap \overline{B})}+\textcolor{olive}{P(\overline{A}\cap \overline{B})} = \textcolor{blue}{P(\overline{B})}}$

In der unteren Zeile siehst du die einzelnen Wahrscheinlichkeiten von Ereignis A. Um die zu bekommen, addierst du ganz einfach die untereinanderstehenden Wahrscheinlichkeiten.

Spalte : $\textcolor{olive}{P (A\cap B)}+ \textcolor{olive}{P (A\cap \overline{B})} = \textcolor{blue}{P(A)}$
Spalte $\overline{A}$ : $\textcolor{olive}{P(\overline{A}\cap B)} + \textcolor{olive}{P(\overline{A}\cap \overline{B})} = \textcolor{blue}{P(\overline{A})}$

In der unteren, rechten Ecke stehen immer 100% oder die gesamte absolute Häufigkeit deines Experiments. Die bekommst du entweder durch addieren der Wahrscheinlichkeiten aus der unteren Zeile:

Untere Zeile: $\textcolor{blue}{P(A)} + \textcolor{blue}{P(\overline{A})}$ = 100%

Oder durch addieren der Wahrscheinlichkeitenaus der rechten Spalte:

Rechte Spalte: $\textcolor{blue}{P(B)} + \textcolor{blue}{P(\overline{B})}$ = 100%

Vierfeldertafel Aufgaben

im Videozur Stelle im Video springen

Schauen wir uns nun verschiedene Vierfeldertafel Aufgaben an.

Aufgaben Vierfeldertafel – Beispiel

Vervollständige die Vierfeldertafel, wenn du folgende Wahrscheinlichkeiten kennst:

$\textcolor{blue}{P(A)=0,45}$
$\textcolor{olive}{P (A\cap \overline{B})=0,2}$
$\textcolor{blue}{P(\overline{B}) = 0,7}}$

Als erstes trägt du die Werte ein, die du kennst. Da deine Werte in der Dezimalschreibweise angegeben sind, übernimmst du sie auf deine gesamte Tabelle. Rechts unten kannst du die 1 hinschreiben.

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} & A & \overline{A} & \\ \hline B & & & \\ \hline \overline{B}& $\textcolor{olive}{0,2}$&&$\textcolor{blue}{0,7}$ \\ \hline &$\textcolor{blue}{0,45}$&&$\textcolor{orange}{1}$& \end{tabular}$

Nun möchtest du die restlichen Felder ausfüllen. Am besten fängst du mit den fehlenden Wahrscheinlichkeiten $\textcolor{blue}{P(B)}$ und $\textcolor{blue}{P(\overline{A})}$ an. Das sind die leeren äußeren Kästchen.

Die Wahrscheinlichkeiten $\textcolor{blue}{P(A)}$ und $\textcolor{blue}{P(\overline{A})}$ müssen zusammen 1 ergeben . Für $\textcolor{blue}{P(\overline{A})}$ rechnest du also:

$\begin{align*} \textcolor{blue}{P(A)} + \textcolor{blue}{P(\overline{A})} &= \textcolor{orange}{1} && |\; - \textcolor{blue}{P(A)}\\ \textcolor{blue}{P(\overline{A})} &= \textcolor{orange}{1} - \textcolor{blue}{0,45}\\ \textcolor{blue}{P(\overline{A})} &= \textbf{0,55} \\ \end{align*}$

Auch die Wahrscheinlichkeiten $\textcolor{blue}{P(B)}$ und $\textcolor{blue}{P(\overline{B})}$ müssen zusammen 1 ergeben. Für $\textcolor{blue}{P(B)}$ rechnest du:

$\begin{align*} \textcolor{blue}{P(B)} + \textcolor{blue}{P(\overline{B})} &= \textcolor{orange}{1}&&|\; - \textcolor{blue}{P(\overline{B})}\\ \textcolor{blue}{P(B)} &= \textcolor{orange}{1} - \textcolor{blue}{P(\overline{B})}\\ \textcolor{blue}{P(B)} &= \textcolor{orange}{1} - \textcolor{blue}{0,7}\\ \textcolor{blue}{P(B)}&=\textbf{0,3} \end{align*}$

Um die restlichen Wahrscheinlichkeiten, zum Beispiel $\textcolor{olive}{P (A\cap B)}$ , zu bestimmen, kannst du genauso vorgehen:

Du weißt, dass du die Wahrscheinlichkeiten $\textcolor{olive}{P (A\cap B)}$ und $\textcolor{olive}{P (A\cap \overline{B})}$ addierst, um $\textcolor{blue}{P(A)}$ zu bekommen. Da dir aber nur noch die Wahrscheinlichkeit $\textcolor{olive}{P (A\cap B)}$ fehlt, stellst du deine Formel nach ihr um.

$\begin{align*} \textcolor{olive}{P (A\cap B)} + \textcolor{olive}{P (A\cap \overline{B})} &= \textcolor{blue}{P(A)}\\ \textcolor{olive}{P (A\cap B)} + \textcolor{olive}{P(A\cap \overline{B})} &= \textcolor{blue}{P(A)}&&|\; -\textcolor{olive}{P(A\cap \overline{B})}\\ \textcolor{olive}{P (A\cap B)} &= \textcolor{blue}{P(A)} - \textcolor{olive}{P(A\cap \overline{B})}\\ \textcolor{olive}{P (A\cap B)} &= \textcolor{blue}{0,45} - \textcolor{olive}{0,2}\\ \textcolor{olive}{P (A\cap B)} &= \textbf{0,25}\\ \end{align*}$

Dasselbe machst du für $\textcolor{olive}{P(\overline{A}\cap \overline{B})}$ :

$\begin{align*} \textcolor{olive}{P(A\cap\overline{B})} + \textcolor{olive}{P(\overline{A}\cap\overline{B})} &= \textcolor{blue}{P(\overline{B})}&&|\;-\textcolor{olive}{P(A)\cap\overline{B})}\\ \textcolor{olive}{P(\overline{A}\cap\overline{B})}&=\textcolor{blue}{P(\overline{B})}-\textcolor{olive}{P(A\cap\overline{B})}\\ \textcolor{olive}{P(\overline{A}\cap\overline{B})}&=\textcolor{blue}{0,7}-\textcolor{olive}{0,2}\\ \textcolor{olive}{P(\overline{A}\cap\overline{B})}&=\textbf{0,5} \end{align*}$

Es fehlt nur noch die Wahrscheinlichkeit $\textcolor{olive}{P(\overline{A}\cap B)}$ :

$\begin{align*} \textcolor{olive}{P (A\cap B)} + \textcolor{olive}{P(\overline{A}\cap B)} &= \textcolor{blue}{P(B)} &&|\; -\textcolor{olive}{P (A\cap B)}\\ \textcolor{olive}{P(\overline{A}\cap B)} &= \textcolor{blue}{P(B)} - \textcolor{olive}{P (A\cap B)}\\ \textcolor{olive}{P(\overline{A}\cap B)} &= \textcolor{blue}{0,3} - \textcolor{olive}{0,25}\\ \textcolor{olive}{P(\overline{A}\cap B)} &= \textbf{0,05} \end{align*}$

Trage nun alle deine Wahrscheinlichkeiten in die Tabelle ein.

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} & A & \overline{A} & \\ \hline B &$\textcolor{olive}{0,25}$&$\textcolor{olive}{0,05}$ &$\textcolor{blue}{0,3}$ \\ \hline \overline{B}& $\textcolor{olive}{0,2}$&$\textcolor{olive}{0,5}$&$\textcolor{blue}{0,7}$ \\ \hline &$\textcolor{blue}{0,45}$&$\textcolor{blue}{0,55}$&$\textcolor{orange}{1}$& \end{tabular}$

Vierfeldertafel Aufgaben – absolute Häufigkeiten

Fülle als nächstes eine Vierfeldertafel mit absoluten Häufigkeiten aus. Dir sind folgende Informationen gegeben:

Am Sportunterricht nehmen insgesamt 25 Kinder teil, von denen 13 weiblich sind. Genau 17 Kinder sind gut im Weitwurf. 10 Mädchen sind gut im Weitwurf.

Definiere als erstes deine Ereignisse:

M = Mädchen
$\overline{M}$ = kein Mädchen / Junge
W = gut in Weitwurf
$\overline{W}$ = schlecht in Weitwurf

Schreibe die Werte auf, die du aus der Aufgabenstellung kennst. Achte darauf, dass du die absoluten Häufigkeiten und nicht die Wahrscheinlichkeiten angibst!

|Ω| = 25 (Insgesamt 25 Kinder im Sportunterricht)
|M| = 13 ( 13 Mädchen im Sportunterricht)
|W| = 17 (17 Kinder gut im Weitwurf)
| $\textcolor{olive}{ M\cap W}$ | = 10 (10 Mädchen sind gut im Weitwurf)

Trage deine Werte in die Vierfeldertafel ein:

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} & W & \overline{W} & \\ \hline M & $\textcolor{olive}{10}$&&$\textcolor{blue}{13}$\\ \hline \overline{M}&&& \\ \hline &$\textcolor{blue}{17}$&&$\textcolor{orange}{25}$& \end{tabular}$

Nun kannst du restlichen Häufigkeiten berechnen. Beginne zum Beispiel mit der Anzahl der Jungs im Sportunterricht. | $\textcolor{blue}{M}$ | und | $\textcolor{blue}{\overline{M}}$ | müssen zusammen |Ω| ergeben. Du rechnest also:

| $\textcolor{blue}{\overline{M}}$ | = 25 – 13 = 12

Berechne nun noch die fehlenden Werte:

| $\textcolor{blue}{\overline{W}}$ | = 25 – 17 = 8

| $\textcolor{olive}{W\cap \overline{M}}$ | = 17 – 10 = 7

| $\textcolor{olive}{M\cap \overline{W}}$ | = 13 – 10 = 3

| $\textcolor{olive}{\overline{M} \cap \overline{W}}$ | = 8 – 3 = 5

Jetzt kannst du deine Werte in die Vierfeldertafel eintragen:

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} & W & \overline{W} & \\ \hline M & $\textcolor{olive}{10}$&$\textcolor{olive}{3}$&$\textcolor{blue}{13}$ \\ \hline \overline{M}&$\textcolor{olive}{7}$&$\textcolor{olive}{5}$&$\textcolor{blue}{12}$ \\ \hline &$\textcolor{blue}{17}$&$\textcolor{blue}{8}$&$\textcolor{orange}{25}$& \end{tabular}$

Vierfeldertafel Aufgaben – relative Häufigkeiten

Im nächsten Beispiel sollst du ebenfalls eine Vierfeldertafel ausfüllen:

Von 50 befragten Personen fahren 13 regelmäßig mit dem Rad und 30 sind männlich. Außerdem fahren 21 Männer nicht regelmäßig mit dem Rad. Wie viele Person sind männlich und fahren regelmäßig Rad?

Zuerst definierst du deine Ereignisse:

R = Radfahrer
$\overline{R}$ = kein Radfahrer
M = Männlich
$\overline{M}$ = nicht männlich/weiblich

Aus der Aufgabenstellung kennst du folgende relative Häufigkeiten:

$\textcolor{blue}{P(R) = \frac{13}{50}}$
$\textcolor{blue}{P(M) = \frac{30}{50}}$
$\textcolor{olive}{P(\overline{R}\cap M) = \frac{21}{50}}$

Trag deine Werte in die Tabelle ein:

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} & R & \overline{R} & \\ \hline M & & $\textcolor{olive}{\frac{21}{50}}$ & $\textcolor{blue}{\frac{30}{50}}$ \\ \hline \overline{M} & & & \\ \hline & $\textcolor{blue}{\frac{13}{50}}$ & & $\textcolor{orange}{\frac{50}{50}}$ \end{tabular}$

Mit den Werten lässt sich nun die Fragestellung beantworten. Um $\textcolor{olive}{P(R\cap M)}$ zu bestimmen, ziehst du $\textcolor{olive}{P(\overline{R}\cap M)}$ von $\textcolor{blue}{P(M)}$ ab. So ergibt sich:

$\begin{align*} \textcolor{olive}{P(R\cap M)} &= \textcolor{blue}{P(M)} - \textcolor{olive}{P(\overline{R}\cap M)}\\ \textcolor{olive}{P(R\cap M)} &= \textcolor{blue}{\frac{30}{50}} -\textcolor{olive}{\frac{21}{50}}\\ \textcolor{olive}{P(R\cap M)} &= \frac{9}{50} \end{align*}$

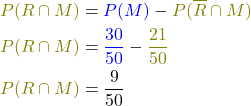
$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} & R & \overline{R} & \\ \hline M & $\textcolor{olive}{\frac{9}{50}}$ & $\textcolor{olive}{\frac{21}{50}}$ & $\textcolor{blue}{\frac{30}{50}}$ \\ \hline \overline{M} & & & \\ \hline & $\textcolor{blue}{\frac{13}{50}}$ & & $\textcolor{orange}{\frac{50}{50}}$ \end{tabular}$

Jetzt weißt du, dass 9 der 50 untersuchten Personen männlich sind und regelmäßig Rad fahren.

Auf dieselbe Weise lassen sich die restlichen Wahrscheinlichkeiten berechnen. Zum Schluss erhältst du folgende Vierfeldertafel:

$\renewcommand{\arraystretch}{1.5} \begin{tabular}[h]{p{2cm}|p{2cm}|p{2cm}|p{2cm}} & R & \overline{R} & \\ \hline M & $\textcolor{olive}{\frac{9}{50}}$& $\textcolor{olive}{\frac{21}{50}}$ & $\textcolor{blue}{\frac{30}{50}}$ \\ \hline \overline{M} & $\textcolor{olive}{\frac{4}{50}}$&$\textcolor{olive}{\frac{16}{50}}$ &$\textcolor{blue}{\frac{20}{50}}$ \\ \hline & $\textcolor{blue}{\frac{13}{50}}$ & $\textcolor{blue}{\frac{37}{50}}$& $\textcolor{orange}{\frac{50}{50}}$ \end{tabular}$

Bedingte Wahrscheinlichkeit Vierfeldertafel

im Videozur Stelle im Video springen

Die Werte, die die Vierfeldertafel zur Verfügung stellt, helfen dir, die bedingte Wahrscheinlichkeit zu berechnen. Dies funktioniert allerdings nur mit relativen Häufigkeiten.

Zur Erinnerung: Die bedingte Wahrscheinlichkeit gibt an, wie wahrscheinlich ein Ereignis ist, unter der Bedingung, dass ein anderes Ereignis bereits eingetreten ist.

Für die bedingte Wahrscheinlichkeit benutzt du folgende Formel:

$\textcolor{purple}{P_A (B)}=\frac{\textcolor{olive}{P(A\cap B)}}{\textcolor{blue}{P(A)}}$

Beide Werte kannst du einfach in der Vierfeldertafel ablesen. Schaue dir dazu nochmal unser Beispiel an:

Du möchtest die Wahrscheinlichkeit berechnen, dass die gewählte Person eine Frau ist ( $P(\overline{M})$ ), unter der Bedingung, dass sie regelmäßig mit dem Rad fährt ( P(R) ). Dazu schaust du zuerst die Wahrscheinlichkeiten $\textcolor{olive}{P (R\cap \overline{M})}$ und $\textcolor{blue}{P(R)}$ aus der Tabelle nach.

$\textcolor{olive}{P (R\cap \overline{M}) = \frac{4}{50}}$
$\textcolor{blue}{P(R) = \frac{13}{50}}$

Jetzt kannst du sie in die Formel einsetzen:

$\textcolor{purple}{P_R (\overline{M})}=\frac{\textcolor{olive}{P (R\cap \overline{M})}}{\textcolor{blue}{P(R)}} = \frac{\textcolor{olive}{\frac{4}{50}}}{\textcolor{blue}{\frac{13}{50}}} = \textcolor{purple}{\frac{4}{13}}$

Die Wahrscheinlichkeit, dass die gewählte Person eine Frau ist, unter der Bedingung, dass sie regelmäßig Fahrrad fährt, liegt bei $\textcolor{purple}{\frac{4}{13}}$ .

Vierfeldertafel — kurz & knapp

Die Vierfeldertafel begegnet dir in der Stochastik. Sie hilft dir, Zusammenhänge zwischen zwei Ereignissen zu erkennen und darzustellen. Sie zeigt nämlich absolute Häufigkeiten oder Wahrscheinlichkeiten der Ereignisse. So kannst du zum Beispiel die Unabhängigkeit von Ereignissen nachweisen.

Quiz zum Thema Vierfeldertafel

Stochastische Unabhängigkeit

Mit den Werten aus der Vierfeldertafel kannst du auch herausfinden, ob zwei Ereignisse stochastisch unabhängig sind. Wie das geht, zeigen wir dir in unserem Video dazu!

Zum Video: Stochastische Unabhängigkeit

zur Videoseite: Vierfeldertafel

Beliebte Inhalte aus dem Bereich Wahrscheinlichkeitsrechnung

Zentraler Grenzwertsatz

Gesetz der großen Zahlen

Laplace Experiment

Bedingte Wahrscheinlichkeit

Vierfeldertafel

Satz der totalen Wahrscheinlichkeit

Stochastische Unabhängigkeit

Tschebyscheff Ungleichung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .