Lotfußpunktverfahren
In diesem Beitrag erklären wir dir, wie du mit dem Lotfußpunktverfahren den Abstand eines Punktes von einer Geraden oder einer Ebene bestimmen kannst und rechnen gemeinsam ausführliche Beispiele durch.
In unserem Erklärvideo findest du eine unkomplizierte und anschauliche Erläuterung der Lotfußpunktverfahren .
Inhaltsübersicht
Lotfußpunktverfahren einfach erklärt
Lotfußpunktverfahren sind ein beliebtes Mittel, um den Abstand zwischen Punkten, Geraden und Ebenen zu berechnen. Der große Vorteil dieser Verfahren ist, dass sie neben dem Abstand auch noch die Koordinaten der Endpunkte (Lotfußpunkte) der Abstandsstrecke liefern. Der Abstand zwischen zwei geometrischen Formen ist dabei:
- Abstand Punkt Gerade : Der Verbindungsvektor steht senkrecht auf der Geraden und verläuft durch den Punkt.
- Abstand Gerade Gerade : Der Verbindungsvektor steht senkrecht auf beiden Geraden.
- Abstand Punkt Ebene : Der Verbindungsvektor steht senkrecht auf der Ebene.
Lotfußpunktverfahren gibt es in zwei Varianten: Entweder verwendet man eine Hilfsebene oder einen allgemeinen, oder „laufenden“, Punkt.
Abstandsrechnung mit dem Lotfußpunktverfahren
Für die Berechnung des Abstandes eines Punktes von einer Geraden stellen wir dir sowohl die Variante mit der Hilfsebene als auch die mit dem laufenden Punkt vor. Außerdem rechnen wir ein Beispiel für beide Varianten ausführlich durch.
Wenn du die Koordinaten des Lotfußpunktes nicht benötigst, erhältst du den Abstand auch schneller durch eine einfache Lösungsformel. In unserem Beitrag Abstand Punkt Gerade erklären wir dir genau, wie du dabei vorgehen musst.
Wenn du dich stattdessen für die Abstandsberechnung anderer geometrischer Formen und Lagen mit dem Lotfußpunktverfahren interessierst, dann schau dir unsere genau passenden Beiträge an:
Mit dem Lotfußpunktverfahren berechnest du den Abstand zwischen einem Punkt und einer Gerade über ein Lot (= eine Gerade, die senkrecht auf der Abstandsgeraden steht). Für die Berechnung verwendest du den Lotvektor.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lotfußpunktverfahren mit einer Hilfsebene
Um mittels des Lotfußpunktverfahrens mit einer Hilfsebene den Abstand zu berechnen, stellst du zunächst die Gleichung einer Hilfsebene auf. Diese Ebene soll senkrecht auf der Geraden stehen und durch den außerhalb liegenden Punkt verlaufen. Anschließend bestimmst du den Durchstoßpunkt der Geraden durch die Hilfsebene. Der Durchstoßpunkt ist dabei derselbe Punkt, der sich beim Fällen des Lotes ergibt.
- Stelle die Hilfsebene
 auf, die den Punkt
auf, die den Punkt  enthält und senkrecht auf der Geraden
enthält und senkrecht auf der Geraden  steht
steht - Bestimme den Schnittpunkt
 der Geraden
der Geraden  und der Ebene
und der Ebene 
- Berechne den Abstand des Punktes zur Geraden:

Lotfußpunktverfahren mit laufendem Punkt
Beim Lotfußpunktverfahren mit einem laufenden Punkt nutzt du die Tatsache, dass der Weg von der Geraden zum außerhalb liegenden Punkt dann am kürzesten ist, wenn der Verbindungsvektor senkrecht auf der Geraden steht. Der Vektor  muss daher orthogonal auf dem Richtungsvektor
muss daher orthogonal auf dem Richtungsvektor  der Geraden stehen. Ein wichtiger Punkt dabei ist, dass orthogonal zueinander stehende Vektoren immer ein Skalarprodukt von Null haben. Über diese Bedingung kann der Lotfußpunkt auf der Geraden berechnet werden.
der Geraden stehen. Ein wichtiger Punkt dabei ist, dass orthogonal zueinander stehende Vektoren immer ein Skalarprodukt von Null haben. Über diese Bedingung kann der Lotfußpunkt auf der Geraden berechnet werden.
- Stelle den allgemeinen Verbindungsvektor
 zwischen dem „laufenden“ Punkt auf der Geraden
zwischen dem „laufenden“ Punkt auf der Geraden  und dem Punkt
und dem Punkt  auf
auf - Bestimme den Lotfußpunkt
 aus der Bedingung
aus der Bedingung 
- Berechne den Abstand des Punktes zur Geraden:

Lotfußpunktverfahren Beispiele
Gegeben ist die Gerade  in Parameterform und der Punkt
in Parameterform und der Punkt  .
.

Wir suchen den minimalen Abstand  zwischen Punkt
zwischen Punkt  und Gerade
und Gerade  .
.
Lösungsweg 1: Lotfußpunktverfahren mit Hilfsebene
Schritt 1: Hilfsebene aufstellen
Die Koordinaten des Richtungsvektors der Geraden  geben die Koeffizienten der Ebenengleichung vor, da die Hilfsebene
geben die Koeffizienten der Ebenengleichung vor, da die Hilfsebene  senkrecht auf
senkrecht auf  stehen soll.
stehen soll.

Da die Hilfsebene zusätzlich den Punkt  enthalten soll, muss die Gleichung
enthalten soll, muss die Gleichung  erfüllen. Wir setzen also die Koordinaten in die Ebenengleichung ein und können dadurch die rechte Seite
erfüllen. Wir setzen also die Koordinaten in die Ebenengleichung ein und können dadurch die rechte Seite  festlegen:
festlegen:

Die Hilfsebene ist damit folgendermaßen definiert:
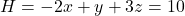
Schritt 2: Schnittpunkt aus Hilfsebene und Gerade berechnen
In diesem Schritt setzt man die Koordinaten von  in
in  ein.
ein.


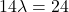

Setzt man dieses  jetzt in g ein, folgt daraus der Schnittpunkt
jetzt in g ein, folgt daraus der Schnittpunkt  .
.
 in
in  :
: 
Der Durchstoßpunkt  liegt somit bei (
liegt somit bei ( ).
).
Schritt 3: Verbindungsvektor  bestimmen und Länge berechnen
bestimmen und Länge berechnen
Um die Länge der Strecke von  (
( ) nach
) nach  zu bestimmen, müssen wir zunächst den Verbindungsvektor
zu bestimmen, müssen wir zunächst den Verbindungsvektor  des Durchstoßpunktes
des Durchstoßpunktes  und des Punktes
und des Punktes  berechnen.
berechnen.

Jetzt können wir über den Betrag des Verbindungsvektors den Abstand  von Punkt und Gerade ausrechnen.
von Punkt und Gerade ausrechnen.

Lösungsweg 2: Lotpunktverfahren mit laufendem Punkt
Schritt 1: Laufenden Punkt und Verbindungsvektor  bestimmen
bestimmen
Den laufenden Punkt entnehmen wir der Geradengleichung. Die Zeilen der Gleichung enstprechen dabei den Koordinaten.

Der allgemeine Verbindungsvektor ergibt sich, indem wir die Punktvektoren  und
und  voneinander abziehen.
voneinander abziehen.

Schritt 2:  und damit den Lotfußpunkt aus der Orthogonalitätsbeziehung (
und damit den Lotfußpunkt aus der Orthogonalitätsbeziehung ( ) des Verbindungsvektors und des Richtungsvektors ableiten
) des Verbindungsvektors und des Richtungsvektors ableiten





Setzten wir  in den laufenden Punkt
in den laufenden Punkt  , so ergibt sich der Lotfußpunkt
, so ergibt sich der Lotfußpunkt  ).
).
Schritt 3: Verbindungsvektor  bestimmen und Länge berechnen
bestimmen und Länge berechnen
Durch Abziehen ihrer Vektoren erhalten wir den Verbindungsvektor zwischen dem Lotfußpunkt  auf der Geraden und dem Punkt
auf der Geraden und dem Punkt  .
.

Der Abstand  ist hier wiederum gleich dem Betrag des Verbindungsvektors
ist hier wiederum gleich dem Betrag des Verbindungsvektors  .
.

Lotfußpunktverfahren — häufigste Fragen
(ausklappen)
Lotfußpunktverfahren — häufigste Fragen
(ausklappen)-
Wie entscheide ich schnell, ob ich die Hilfsebene oder den laufenden Punkt nehmen sollte?Nimm meist den laufenden Punkt, wenn die Gerade in Parameterform vorliegt und du sicher im Skalarprodukt bist. Die Hilfsebene ist oft schneller, wenn du gerne Schnittpunkte berechnest oder eine Ebenengleichung schnell aufstellen kannst. Beide Wege liefern denselben Lotfußpunkt und Abstand.
-
Wie kann ich prüfen, ob mein berechneter Lotfußpunkt wirklich auf der Geraden liegt?Du prüfst es, indem du kontrollierst, ob der Lotfußpunkt die Geradengleichung erfüllt. Setze die Koordinaten in
 ein und schau, ob es ein passendes
ein und schau, ob es ein passendes  gibt. Zusätzlich gilt als Check:
gibt. Zusätzlich gilt als Check:  .
.
-
Welche Rechenfehler passieren beim Skalarprodukt am häufigsten?Am häufigsten werden Vorzeichen falsch übernommen oder Klammern beim Ausmultiplizieren vergessen. Auch typisch ist, dass nur zwei statt drei Komponenten multipliziert werden oder der Richtungsvektor falsch abgeschrieben wird. Achte darauf, wirklich komponentenweise zu rechnen:
 .
.
-
Wie gehe ich vor, wenn die Gerade nicht in Parameterform gegeben ist?Du bringst die Gerade zuerst in Parameterform, indem du einen Punkt auf der Geraden und einen Richtungsvektor bestimmst. Bei zwei Punkten ist
 . Bei zwei Ebenen (Schnittgerade) bekommst du
. Bei zwei Ebenen (Schnittgerade) bekommst du  über das Kreuzprodukt der Normalenvektoren:
über das Kreuzprodukt der Normalenvektoren:  .
.
-
Wie bestimmte ich den Abstand Punkt-Ebene mit dem „laufenden Punkt“?Du nimmst einen laufenden Punkt
 in der Ebene und nutzt den Normalenvektor
in der Ebene und nutzt den Normalenvektor  der Ebene als Orthogonalitätsrichtung. Stelle
der Ebene als Orthogonalitätsrichtung. Stelle  auf und fordere
auf und fordere  , also dass
, also dass  zusammen mit „
zusammen mit „ in der Ebene liegt“. Dann ist
in der Ebene liegt“. Dann ist  .
.
Abstandsrechnungen in der Geometrie
Abstände kannst du in der Geometrie zwischen verschiedenen Objekten bestimmen. Zum Glück haben wir zu all diesen Themen eigene Beiträge für dich:
- Abstand zwischen zwei Punkten (Abstand zweier Punkte )
- Abstand zwischen einem Punkt und einer Geraden (Abstand Punkt Gerade )
- Abstand zwischen zwei Geraden (Abstand Gerade Gerade
)
- wenn die Geraden parallel verlaufen (Abstand Gerade Gerade )
- wenn die Geraden windschief zueinander stehen (Abstand windschiefer Geraden )
- Abstand zwischen einem Punkt und einer Ebene (Abstand Punkt Ebene )

