Parallele Geraden

Parallele Geraden — einfach erklärt

Parallele Geraden sind zwei Linien, die sich niemals schneiden. Das bedeutet, sie haben überall den gleichen Abstand zueinander, egal wo du misst. Du kannst sie dir wie Bahngleise vorstellen, die immer nebeneinander verlaufen. Egal, wie weit du diesen Geraden folgst, sie bleiben immer gleich weit voneinander entfernt.

direkt ins Video springen

In Mathe nutzt du das Zeichen || , um die Parallelität zwischen zwei Geraden zu beschreiben. Zum Beispiel: g || f

Parallele Geraden zeichnen

Um parallele Geraden zu zeichnen gibt es zwei Methoden. Für beide brauchst du nur dein Geodreieck und einen Stift: 

1. Methode: Querstreifen vom Geodreieck anlegen
2. Methode: Mittellinie vom Geodreieck anlegen 

Möglichkeit 1

Für die erste Methode nutzt du die parallelen Hilfslinien auf deinem Geodreieck. Dabei gehst du so vor:

1. Anlegen: Lege das Geodreieck so an die gegebene Gerade, dass eine der parallelen Linien auf dem Geodreieck genau auf der Geraden liegt.
   

   

   direkt ins Video springen

2.  Neue Gerade zeichnen: An der neuen Position zeichnest du entlang des Geodreiecks eine neue Gerade. Diese neue Gerade bezeichnest du mit f. Sie ist parallel zur ursprünglichen Gerade g.

direkt ins Video springen

Tipp: Zwischen den parallelen Linien auf deinem Geodreieck befinden sich weitere kleine Hilfsstriche. Sie dienen dir als Lineal. So kannst du zum Beispiel einen Abstand von genau 1,7 cm zwischen den Geraden zeichnen.

Möglichkeit 2

Bei der zweiten Methode nutzt du die Mittellinie vom Geodreieck, wo 90° dran steht. Hier gehst du wie folgt vor:

1. Senkrechte zeichnen: Lege die Mittellinie vom Geodreieck an die gegebene Gerade. Zeichne eine dünne Bleistiftlinie von der Geraden aus nach links oder nach rechts — je nachdem wo du die parallele Gerade haben willst. Falls nötig kannst du auch einen bestimmten Abstand abmessen z. B. 3 cm.
   

   

   direkt ins Video springen

2. Neue Gerade zeichnen: Nun setzt du an der dünnen Hilfslinie wieder die Mittellinie vom Geodreieck an und zeichnest die neue parallele Gerade. Anschließend radierst du deine Hilfslinie natürlich weg.
   

   

   direkt ins Video springen

Tipp: Mit dem Geodreieck kannst du von der Mittellinie nur einen Abstand von maximal 8 cm zeichnen. Wenn du einen größeren Abstand zwischen den Parallelen brauchst, setzt du nach Schritt 1 ein Lineal an deine Hilfslinie und verlängerst sie. Dann kannst du weiter mit Schritt 2 fortfahren.

Parallele Geraden erkennen

Parallele Geraden erkennst du nicht nur am gleichen Abstand zueinander. Im Koordinatensystem kannst du parallele Geraden daran erkennen, dass sie die gleiche Steigung haben.

Die Steigung einer Geraden gibt an, wie stark die Gerade ansteigt oder abfällt. Wie stark eine Gerade ansteigt oder abfällt, siehst du in der Geradengleichung y = m • x + t. Dort steht das „m“ nämlich für die Steigung. Haben zwei Geraden also denselben Wert für „m“, sind sie parallel. Es gilt also: m₁ = m₂

direkt ins Video springen

Im Bild siehst du zum Beispiel die Geraden g = 3 • x + 1 und h = 3 • x – 4. Beide haben die Steigung 3 und sind daher parallel.

Gut zu wissen: Sind zwei Geraden nicht parallel zueinander, verwendest du das Zeichen .

Parallele Gerade bestimmen

Es kann auch vorkommen, dass du eine parallele Gerade ohne den Abstand bestimmen musst. Dafür brauchst du die Geradengleichung y = m • x + t. Es kann aber auch ein Punkt gegeben sein, durch den du eine parallele Gerade zeichnen sollst. 

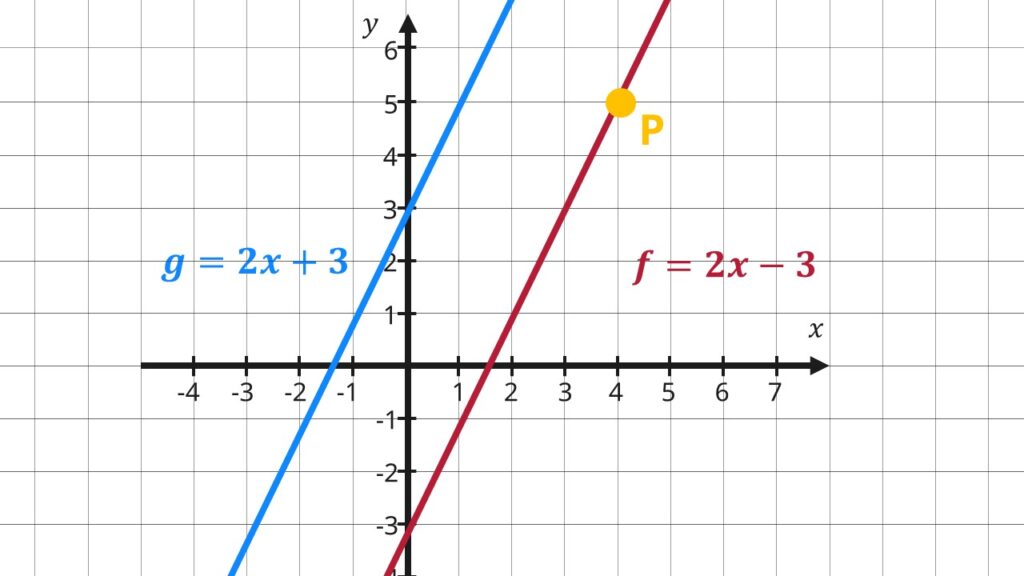
Zum Beispiel hast du die Gerade g = 2 • x + 3 und den Punkt P (4 | 5) gegeben. Um eine parallele Gerade f durch P zu zeichnen, gehst du wie folgt vor:

1. Bestimme die Steigung der gegebenen Geraden. In der Geradengleichung steht immer das „m“ für die Steigung. In unserem Beispiel ist das also 2.
    
   g = 2 • x + 3 → Steigung = 2
    
2. Da parallele Geraden immer die gleiche Steigung haben, kennst du jetzt die Steigung für deine neue Gerade f:
    
   f = 2 • x + t
    
3. Jetzt fehlt dir nur noch der Schnittpunkt mit der y-Achse t. Dafür brauchst du den Punkt P, durch den die Gerade f verlaufen soll. Du setzt daher die Koordinaten von P in die Geradengleichung von f ein und löst nach t auf:
    
   5 = 2 • 4 + t
   5 = 8 + t          | – 8
   t = -3
   

   

   direkt ins Video springen

4. Nun kennst du die Geradengleichung für deine zu g parallele Gerade f, nämlich: f = 2 • x -3. Um die Gerade in das Koordinatensystem zu zeichnen, markierst du den Schnittpunkt t — in dem Fall -3 an der y-Achse. Dann zeichnest du mit dem Lineal eine Gerade durch diesen Punkt und den Punkt P.

Parallele Geraden — Übungen

Übungen helfen dir, das Thema besser zu verstehen und anzuwenden. Hier sind einige Aufgaben, mit denen du dein Wissen über parallele Geraden vertiefen kannst.

Aufgabe 1: Fehlenden Anstieg bestimmen

Gegeben sind die Geraden:

• g = 3 • x + 2
• h $=m\; •x-1$

Bestimme den Anstieg für die Gerade h, sodass die Geraden parallel sind.

Lösung: m = 3, weil bei parallelen Geraden der Anstieg gleich sein muss

Aufgabe 2: Steigung paralleler Geraden

Gegeben ist die Gerade g = 2 • x + 2. Finde die Gleichung einer Geraden h, die parallel zu g verläuft und durch den Punkt (1 |3) geht.

direkt ins Video springen

Lösung: 

1. Bestimme die Steigung der gegebenen Geraden g. Die Steigung m ist 2.
2. Setze die Steigung und die Koordinaten des Punktes in die Geradengleichung ein, um den Schnittpunkt mit der y-Achse t zu finden:
   3 = 2 • 1 + t
   3 = 2 + t        | – 2
   t = 1
3. Die Gleichung der neuen Geraden lautet: h = 2 • x + 1

Schnittpunkt zweier Geraden

Verlaufen zwei Geraden nicht parallel zueinander, schneiden sie sich in einem Punkt. Wie du den Schnittpunkt von zwei Geraden berechnest, zeigen wir dir in unserem Video!