Phi Koeffizient
In diesem Beitrag werden wir den Phi Koeffizient berechnen. Anhand eines anschaulichen Beispiels ist im Anschluss auch die Phi Koeffizient Interpretation ein Leichtes!
Kleinphi macht auch Mist? Nicht mit uns! Nach unserem Video bereitet dir der Phi Koeffizient keine Sorgen mehr.
Inhaltsübersicht
Phi Koeffizient einfach erklärt
Zuallererst solltest du wissen, dass der Phi Koeffizient nur für binäre Variablen geeignet ist. Binär oder auch dichotom bedeutet, dass die Variable nur zwei verschiedene Ausprägungen besitzt. Ist das der Fall, ist dieser Koeffizient ein einfaches Maß, um den Zusammenhang zweier Variablen zu beschreiben.
Wie genau das geht, zeigen wir dir an folgender Vier Felder Tafel:
Es wurden 50 Personen nach ihrem Geschlecht und, ob sie Raucher oder Nicht-Raucher sind, befragt. Nun interessiert uns, ob ein Zusammenhang zwischen dem Geschlecht und dem aktiven Tabakkonsum besteht.
Phi Koeffizient berechnen
Dazu nutzen wir diese Formel:
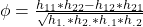
Du hast keine Ahnung, was diese ganzen h’s bedeuten? Keine Sorge, diese Bezeichnungen werden dir im Video Kontingenztabelle erklärt.
Zur Berechnung kannst du die entsprechenden Werte aus der Tabelle einfach in die Formel einsetzen:
Das war’s schon! Unser Ergebnis lautet 0,035.
Phi Koeffizient Interpretation
Anders als der Chi Quadrat Koeffizient , kann der Phi Koeffizient auch negative Werte bis -1 annehmen. Aber auch hier drückt ein Wert von 0 keinen und ein Wert von 1 bzw. -1 einen perfekten Zusammenhang aus.
In unserem Beispiel besteht also fast kein Zusammenhang zwischen dem Geschlecht und dem Rauchen.
Du siehst, dieser Koeffizient lässt sich sehr einfach berechnen. Er bietet sich also perfekt dafür an Zusammenhänge für zwei binäre Variablen zu interpretieren. Binär heißt, dass die betrachteten Variablen jeweils nur 2 verschiedene Ausprägungen haben. Die Informationen fasst man in diesem Fall am Besten in einer 2 mal 2 Kontingenztabelle, also einer Vier Felder Tafel zusammen und berechnet den Zusammenhang wie oben beschrieben. Merk‘ dir einfach die Bezeichnung der einzelnen Zellen, dann ist der Weg zu einer richtigen Lösung nicht weit.
Möchte man den Zusammenhang von Daten komplexerer Kontingenztabellen berechnen, muss man auf den Chi Quadrat Koeffizient oder den Kontingenzkoeffizient ausweichen.