Kontingenzkoeffizient
Hier erfährst du alles über den Kontingenzkoeffizient. Wir legen den Fokus auf die Schritte den korrigierten Kontingenzkoeffizient zu berechnen und auf die anschließende Kontingenzkoeffizient Interpretation.
Du hast heute schon genug gebüffelt? Unser Video erklärt dir alles zum Kontingenzkoeffizient effektiv in wenigen Minuten!
Inhaltsübersicht
Kontingenzkoeffizient einfach erklärt
Der korrigierte Kontingenzkoeffizient beschreibt die Stärke des Zusammenhangs zweier Merkmale eines beliebigen Skalenniveaus . Normalerweise wird der Kontingenzkoeffizient auf Basis der Daten einer Kontingenztabelle und des Chi Quadrat Koeffizienten berechnet und kann deshalb als dessen Fortsetzung betrachtet werden.
Kontingenzkoeffizient berechnen
Wie wir eben schon erwähnt haben, ist der Kontingenzkoeffizient die Fortsetzung des Chi Quadrat-Koeffizienten. Noch nie gehört? Dann schau dir noch schnell unser Video dazu an. Der Chi-Quadrat-Koeffizient bereitet dir keine Schwierigkeiten mehr? Prima, dann wagen wir uns jetzt zum Kontingenzkoeffizienten vor!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Chi Quadrat Kontingenzkoeffizient
Im Folgenden werden wir nur den Kontingenzkoeffizienten berechnen und den Chi Quadrat Koeffizienten als gegeben annehmen. Aber Achtung! In der Klausur musst du sehr wahrscheinlich in der Lage sein, Beide zu berechnen.
Wir nehmen also an, dass unser Chi-Quadrat Koeffizienten 148.42 beträgt.
Kontingenzkoeffizienten Formel
Um nun den Kontingenzkoeffizienten C zu berechnen, brauchst du diese Formel:
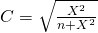
Der Wertebereich von C liegt zwischen 0 und C max ![Rendered by QuickLaTeX.com C\in\ \left[0;C_{max}\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e264f5ab7aa17b540c42146de7ccf268_l3.png) . Was es mit C max auf sich hat, erklären wir dir gleich. Zuerst berechnen wir aber unser C:
. Was es mit C max auf sich hat, erklären wir dir gleich. Zuerst berechnen wir aber unser C:
Das N aus unserem Beispiel beträgt 400. Also haben wir alle Werte bereits gegeben und müssen diese nur noch einsetzen.
Wir erhalten 0,52. Jetzt errechnen wir noch C max: Die Formel hierzu lautet:

m steht hierbei für das Minimum deiner Zeilen- beziehungsweise Spaltenanzahl. Es kommt eben darauf an, was kleiner ist. Hast du beispielsweise eine Tabelle mit fünf Zeilen und nur zwei Spalten, so wäre dein m gleich zwei.
Da wir in unserem Beispiel eine gleiche Anzahl an Zeilen und Spalten haben, müssen wir hier keine Unterscheidung treffen und unser m ist gleich drei. Wir haben also ein C max von 0,82:

So. Nun haben wir ein C und ein C max. Aber was bringen uns diese Ergebnisse jetzt?
Korrigierter Kontingenzkoeffizient
Ganz einfach. In unserem letzten Schritt teilen wir C durch C max und erhalten dadurch den normierten Kontingenzkoeffizienten.
Nun wollen wir aber noch den normierten Koeffizienten für unser Beispiel berechnen:
Das Ergebnis ist 0,63. Unsere Variablen haben also einen eher starken Zusammenhang.
Kontingenzkoefizient Interpretation
Der normierte Kontingenzkoeffizient ermöglicht im Gegensatz zum Chi Quadrat Koeffizient eine genaue Interpretation des Zusammenhangs. Er liegt nämlich immer zwischen null und eins.
Hast du ein Ergebnis von null, sind deine Variablen komplett unabhängig, bei einem Ergebnis von eins, komplett abhängig voneinander. Klingt logisch, oder?
Wir erinnern uns: für den normierten Kontingenzkoeffizienten brauchen wir den Chi Quadrat Koeffizienten, den Kontingenzkoeffizienten und sein Maximum. Die Berechnung ist zwar sehr zeitaufwendig, dafür aber ziemlich einfach. Wenn du jeden Schritt konzentriert durchführst, kommst du garantiert immer auf das richtige Ergebnis.


