Varianz berechnen
Dieser Artikel zeigt dir wie du die Varianz berechnen kannst. Wir erklären dir die Formel anhand von drei einfachen Beispielen und gehen auf den Verschiebungssatz zur Varianz ein.
Du willst das Thema gut erklärt bekommen? Dann lehn‘ dich zurück und schau‘ dir unser Video dazu an! Als Grundlage empfehlen wir dir unseren Beitrag zur Varianz . Auch zum Thema Stichprobenvarianz haben wir ein Video für dich.
Inhaltsübersicht
Varianz berechnen Vorgehen
Um die Varianz zu berechnen, gibt es ein ganz einfaches Vorgehen.
- Den Mittelwert (Durchschnitt) ausrechnen
- Die Werte des Zufallsexperiments in die Formel zur Varianz einsetzen
- Die Varianz berechnen
Falls du dir nicht mehr sicher bist, wie du das arithmetische Mittel ausrechnest und was der Unterschied zum Erwartungswert ist, schau dir unsere Videos dazu an.
Varianz Formel
Die Formel zur Varianz schaut kompliziert aus, ist aber sehr einfach anzuwenden.
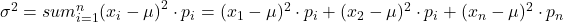
-
 ist das Zeichen für die Varianz (bei Zufallsexperimenten)
ist das Zeichen für die Varianz (bei Zufallsexperimenten) -
 ist der Mittelwert, bzw. Erwartungswert
ist der Mittelwert, bzw. Erwartungswert
-
 ist das Ergebnis des Zufallsexperiments
ist das Ergebnis des Zufallsexperiments
-
 beschreibt, dass erst eine Summe der gewichteten quadratischen Abweichungen vom Mittelwert berechnet wird
beschreibt, dass erst eine Summe der gewichteten quadratischen Abweichungen vom Mittelwert berechnet wird -
 steht für die Wahrscheinlichkeit eines Ereignisses
steht für die Wahrscheinlichkeit eines Ereignisses  . Es handelt sich also um einen Gewichtungsfaktor.
. Es handelt sich also um einen Gewichtungsfaktor.
Du kannst dir also merken, dass du die Varianz berechnen kannst, indem du die Summe der gewichteten quadrierten Abweichungen aller Messwerte vom Mittelwerte bildest. Mit dem nächsten Beispiel wird das Ganze deutlicher.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel Varianz berechnen
Stell dir vor, du misst eine Woche lang im Sommer immer mittags die Temperatur und erhältst folgende Werte:
| Wochentag | Mo | Di | Mi | Do | Fr | Sa | So |
| Temperatur Maximal | 28 | 29 | 27 | 21 | 18 | 28 | 24 |
Wie kannst du für diese Werte die Varianz berechnen?
Zuerst musst du den Durchschnitt ermitteln. Dafür zählst du die einzelnen Temperaturwerte zusammen, also addierst sie. Diese Summe teilst du dann durch die Anzahl der Werte, die wir haben. In unserem Fall sieben, da du für jeden Wochentag einen Wert hast. Das ergibt eine Durchschnittstemperatur von 25 Grad. Mathematisch sieht das so aus:

Danach kannst du jetzt die entsprechenden Werte in die Formel zur Varianz einsetzen und so diese berechnen. Von deinen Temperaturwerten ziehst du jeweils den Mittelwert ab. Was dabei rauskommt quadrierst du, also rechnest es hoch zwei. Du ermittelst also die Abweichung deines Wertes vom Mittelwert und quadrierst dann diese Abweichung. Anschließend musst du die Abweichung noch mit der relativen Häufigkeit gewichten. Diese ist in diesem Beispiel  , da es pro Tag einen Messwert gibt. Das Ganze wiederholst du für jeden Wert – bei unserem Beispiel also sieben mal – und bildest daraus eine Summe. Wenn du die einzelnen Werte in die Formel einsetzt, sieht das so aus:
, da es pro Tag einen Messwert gibt. Das Ganze wiederholst du für jeden Wert – bei unserem Beispiel also sieben mal – und bildest daraus eine Summe. Wenn du die einzelnen Werte in die Formel einsetzt, sieht das so aus:

Zuletzt willst du die Varianz berechnen. Als Zwischenschritt kannst du erst die Werte in den Klammern ausrechnen.

Danach quadrierst du die Abweichungen und siehst den Faktor zusammen.
zusammen.

Am Schluss erhältst du eine mittlere quadratische Abweichung, also eine Varianz von 14,86 Grad hoch zwei.
Die Varianz ist schwer zu interpretieren, da sie ein Quadrat der Abweichung vom Mittelwert darstellt. Um die Zahl besser nachvollziehen zu können, schau dir an, wie du die Standardabweichung berechnen kannst.
Beispiel Varianz berechnen Würfel
Schauen wir uns gleich noch ein weiteres Beispiel an. Stell dir vor, du wirfst einen 6 – seitigen Würfel 15 mal und schreibst dir die Ergebnisse auf:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Anzahl | 2 | 3 | 2 | 4 | 3 | 1 |
| P(X) | 2/15 | 3/15 | 2/15 | 4/15 | 3/15 | 1/15 |
Um die Varianz zu berechnen ist das Vorgehen wie beim vorigen Beispiel. Zuerst bestimmst du den Mittelwert für deine Daten. Die relativen Häufigkeiten sind in der Tabelle schon gegeben.

Wir erhalten also einen Mittelwert von 3,4. Das ist nicht der Erwartungswert eines Würfels, sondern nur der Mittelwert für unsere geworfenen Zahlen! Nun müssen wir die einzelnen Werte aus unserer Tabelle in die Formel einsetzen. Dafür ziehen wir von jedem Ergebnis den Erwartungswert ab. Dann quadrieren wir das Ergebnis. Diesen Schritt müssen wir für alle 15 Werte durchführen und sie schließlich noch addieren. Am Schluss dürfen wir nicht vergessen, durch 15 zu teilen, da wir ja die durchschnittliche Abweichung berechnen. In unserer Formel steht dies im ersten Bruch ganz vorne. Wenn wir die Werte in die Formel der Varianz einsetzen, ergibt sich:

Um die Varianz berechnen zu können, lösen wir wieder zuerst die Klammern auf.

Dann rechnen wir die Abweichungen hoch zwei und gewichten diese.


Schließlich ergibt sich eine Varianz von 2,24 Würfelaugen im Quadrat. Du siehst, bei größeren Werten ist es ganz schön viel Schreibarbeit die Varianz zu berechnen. Doch dafür gibt es einen Trick: den Verschiebungssatz.
Varianz berechnen — häufigste Fragen
(ausklappen)
Varianz berechnen — häufigste Fragen
(ausklappen)-
Wie berechne ich die Varianz Schritt für Schritt?Du berechnest die Varianz, indem du zuerst den Mittelwert
 bestimmst. Danach ziehst du von jedem Wert
bestimmst. Danach ziehst du von jedem Wert  den Mittelwert ab, quadrierst die Abweichung und gewichtest sie mit
den Mittelwert ab, quadrierst die Abweichung und gewichtest sie mit  . Am Ende addierst du alles:
. Am Ende addierst du alles:  .
.
-
Was bedeuten die Symbole in der Varianzformel
 ?
?
 ist die Varianz, also die mittlere quadratische Abweichung vom Mittelwert.
ist die Varianz, also die mittlere quadratische Abweichung vom Mittelwert.  ist der Mittelwert bzw. Erwartungswert,
ist der Mittelwert bzw. Erwartungswert,  sind die möglichen Ergebnisse.
sind die möglichen Ergebnisse.  ist die Wahrscheinlichkeit (oder relative Häufigkeit) des Ergebnisses
ist die Wahrscheinlichkeit (oder relative Häufigkeit) des Ergebnisses  . Die Summe addiert alle gewichteten, quadrierten Abweichungen.
. Die Summe addiert alle gewichteten, quadrierten Abweichungen.
-
Wie komme ich bei Messwerten auf die Gewichtung
 ?
Du nimmst als Gewichtung
?
Du nimmst als Gewichtung die relative Häufigkeit eines Werts. Wenn jeder Messwert genau einmal vorkommt, ist
die relative Häufigkeit eines Werts. Wenn jeder Messwert genau einmal vorkommt, ist  für jeden Wert gleich. Im Temperaturbeispiel gibt es 7 Tage mit je einem Wert, deshalb gilt für jeden Tag
für jeden Wert gleich. Im Temperaturbeispiel gibt es 7 Tage mit je einem Wert, deshalb gilt für jeden Tag  .
.
-
Was ist der Verschiebungssatz zur Varianz?Der Verschiebungssatz ist eine Rechenformel, mit der du die Varianz oft schneller ausrechnen kannst:
 . Du berechnest also zuerst den Erwartungswert der quadrierten Werte und ziehst davon das Quadrat des Erwartungswerts ab.
. Du berechnest also zuerst den Erwartungswert der quadrierten Werte und ziehst davon das Quadrat des Erwartungswerts ab.
-
Wie wende ich den Verschiebungssatz beim Würfelbeispiel an?Du berechnest zuerst
 , indem du
, indem du  jeweils mit ihrer relativen Häufigkeit (z. B.
jeweils mit ihrer relativen Häufigkeit (z. B.  ) multiplizierst und alles addierst. Danach ziehst du
) multiplizierst und alles addierst. Danach ziehst du  ab, also hier
ab, also hier  . So erhältst du wieder
. So erhältst du wieder  .
.
Varianz berechnen Verschiebungssatz
Der Verschiebungssatz hilft dir dabei, die Varianz für größere Datenmengen ausrechen.

Im Prinzip wird hier der Erwartungswert aus der Formel für die Varianz ausgeklammert. Trotzdem rechnest du weiterhin die Varianz aus. Beachte hier auch die Schreibweise: Einmal ist das hoch zwei innerhalb der Klammer und einmal außerhalb. Die Formel erschließt sich am besten mit einem Beispiel.
Verschiebungssatz Beispiel
Schauen wir uns dafür noch einmal unser Würfel Beispiel an.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Anzahl | 2 | 3 | 2 | 4 | 3 | 1 |
| P(X) | 2/15 | 3/15 | 2/15 | 4/15 | 3/15 | 1/15 |
- Der Mittelwert unseres Zufallsexperiments ist wieder 3,4.
- Um die Varianz zu berechnen, wenden wir nun jedoch die Formel für den Verschiebungssatz an.
Dafür setzen wir für das erste X die unterschiedlichen Würfelwerte eine, also 1, 2, 3, 4, 5, 6 und quadrieren diese. Dann multiplizieren wir die Teilergebnisse mit der relativen Häufigkeit. Diese steht ebenfalls in der Tabelle. Nachdem wir aus diesen Werten eine Summe gebildet haben, ziehen wir davon den quadrierten Erwartungswert ab.

Der Verschiebungssatz liefert das gleiche Ergebnis wie die Berechnung über die Formel der Varianz.