Geometrisches Mittel
Hier erhältst du eine Antwort auf die Frage „Was ist das geometrische Mittel“? Als geometrisches Mittel wird ein weiterer wichtiger Mittelwert in der deskriptiven Statistik bezeichnet. Wie du das geometrische Mittel berechen kannst, zeigen wir dir in diesem Beitrag!
Lange Beschreibungen und unübersichtliche Formeln sind nichts für dich? Unser Video zum Thema verschafft Abhilfe und erklärt dir unter anderem die Punkte geometrisches Mittel Formel und Berechnung anschaulich an einem Beispiel!
Inhaltsübersicht
Geometrisches Mittel einfach erklärt
Das geometrische Mittel, auch mittlere Proportionale genannt, ist ein Lagemaß von quantitativen Beobachtungswerten der deskriptiven Statistik. Man erhält ihn durch die Berechnung der n-ten Wurzel aus dem Produkt der betrachteten positiven Zahlenwerte. Einfach gesagt bedeutet das, dass du mit dem geometrischen Mittel zum Beispiel die durchschnittliche prozentuale Veränderungen von Wachstumsraten bestimmen kannst.
Geometrisches Mittel Statistik
Dieser Mittelwert ist stets kleiner oder gleich dem arithmetischen Mittel. Allgemein ist die Aufgabe der deskriptiven Statistik umfangreiche Mengen an Daten durch Maßzahlen zusammenzufassen. Komplexe Sachverhalte sollen so möglichst geordnet und übersichtlich dargestellt werden.
Geometrisches Mittel Anwendung
Das geometrische Mittel als Lageparameter gehört folglich zu den Mittelwerten und wird bei der Berechnung von prozentualen Veränderungen verwendet. Wenn man beispielsweise mit Wachstumsraten wie Preissteigerungen oder Zinsraten zu tun hat, sollte man dieses Mittel hernehmen. Irrtümlicherweise wird hierfür häufig das arithmetische Mittel verwendet.
Geometrisches Mittel berechnen
Bei der Berechnung muss man unterscheiden, ob es sich bei den vorhandenen Daten um Beobachtungswerte oder und absolute und relative Häufigkeiten handelt. Letzteres bezeichnet man als gewogenes geometrisches Mittel. Handelt es sich um Beobachtungswerte spricht man von einem ungewogenen geometrischem Mittel.
Gewogenes geometrisches Mittel
Bei der Berechnung des gewogenen geometrischen Mittels müssen die Wahrscheinlichkeiten der Häufigkeiten noch zusätzlich berücksichtigt werden. Die Formel bleibt grundsätzlich die selbe, lediglich steht im Exponenten jedes Faktors seine absolute Häufigkeit. Einfach gesagt heißt das, dass du jeden Wert mit seiner Wahrscheinlichkeit hoch nimmst vor der Multiplikation.
Geometrisches Mittel negative Zahlen
Was man außerdem wissen muss ist, dass keiner der Werte negativ sein darf. So wird ein insgesamt negatives Vorzeichen unter der Wurzel zu vermieden. Außerdem darf keiner der Werte 0 sein, da auch in diesem Fall die Berechnung nicht möglich wäre. Durch die Multiplikation wäre das Gesamtergebnis ebenfalls 0.
Geometrisches Mittel Beispiel
Wie vorhin bereits erwähnt wird das geometrische Mittel in der Praxis zur Berechnung von prozentualen Veränderungen von Zahlenreihen verwendet. Mit diesem Lagemaß der Statistik können durchschnittliche Wachstumsfaktoren berechnet werden. Ein Beispiel aus der Praxis sind unter anderem Zinsraten, das Wachstum des BIP oder das durchschnittliche Wachstum von Unternehmensgewinnen.
Geometrisches Mittel Wachstumsfaktor
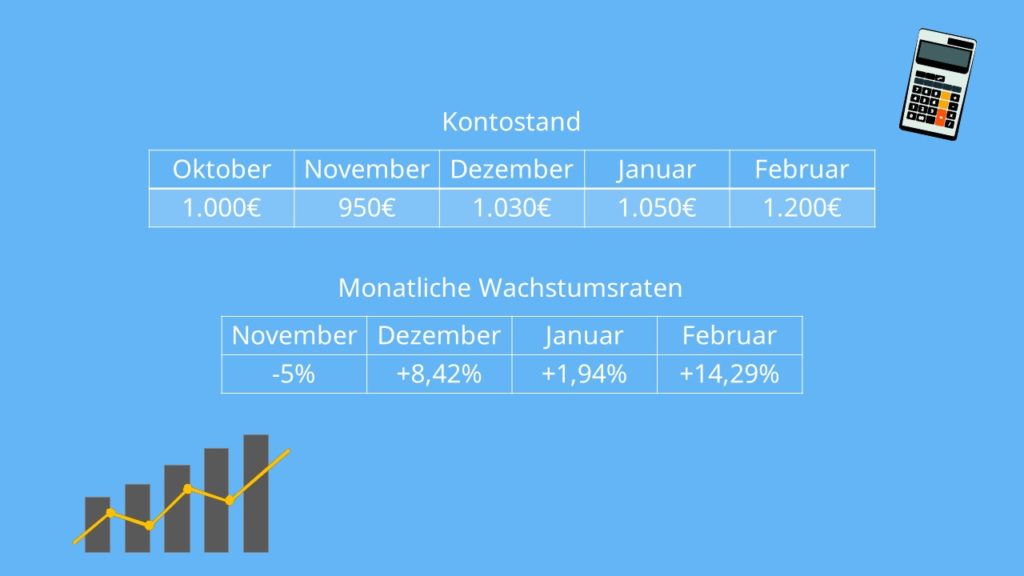
Um das Ganze verständlicher zu machen, erklären wir dir die Berechnung direkt an einem Beispiel: Stell dir vor, dein Kontostand entwickelt sich während des Semesters folgendermaßen:
Du hast also von Monat zu Monat diese Wachstumsraten:
Jetzt möchtest du gerne wissen, um wieviel Prozent sich dein Konto durchschnittlich verändert hat. Und für genau so einen Fall gibt es das geometrische Mittel. Es ist sehr wichtig darauf zu achten die Auf- beziehungsweise Abzinsungsfaktoren und nicht die Verzinsungen zu multiplizieren. Andernfalls erhälst du ein falsches Ergebnis.
Wir rechnen also:
![Rendered by QuickLaTeX.com {\bar{x}}_{geom}=\ \sqrt[4]{0,95*1,0842*1,0194*1,1429}\ \approx1,047](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-174fb0de02c57cc77e525c37475f547b_l3.png)
Du siehst, das Vermögen auf deinem Konto ist während des Semesters um durchschnittlich 4,7% gestiegen. Um dein Ergebnis zu überprüfen, kannst du auch nochmal gegenrechnen:
Tada, du kommst auf die gleiche Lösung!
Geometrisches Mittel Mittenfrequenz 
Ein weiteres Beispiel ist die sogenannte Mittenfrequenz 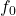 : sie ist das geometrische Mittel aus der unteren und der oberen Grenzfrequenz
: sie ist das geometrische Mittel aus der unteren und der oberen Grenzfrequenz 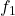 und
und 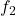 eines Frequenzbands mit einer festgelegten Filterbandbreite. Sie berechnet sich wie folgt:
eines Frequenzbands mit einer festgelegten Filterbandbreite. Sie berechnet sich wie folgt:
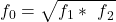
Hier wäre es falsch das arithmetische Mittel für beide Grenzfrequenzen herzunehmen. Generell verwendet man das geometrische Mittel in dem Fall, dass sich der Unterschied zweier Größen eines Merkmals besser über Quotienten als über Differenzen beschreiben lässt.
Jetzt weißt du, dass das geometrische Mittel einfach die prozentuale Veränderung einer Zahlenreihe wiedergibt.