Mittelwert, Median & Modus
Du willst den Unterschied zwischen Mittelwert, Median und Modus verstehen? In unserem Artikel und im Video erfährst du alles, was du zu den drei Lageparametern wissen musst!
Inhaltsübersicht
Modus, Median, Mittelwert — Was ist der Unterschied?
Schau dir Modus, Median und Mittelwert gleich an einem Beispiel an. Hier siehst du die Noten von 5 Schülern in einer Prüfung:
| Anna | Tobias | Lisa | Linus | Marie |
| 1 | 1 | 2 | 4 | 5 |
- Der Modus ist einfach die häufigste Note, hier also die 1.
- Der Median liegt genau in der Mitte der Tabelle, wenn du die Noten der Reihe nach sortierst. Hier ist der Median also 2.
- Der Mittelwert ist der Durchschnitt der Noten. Um ihn zu berechnen, zählst du alle Noten zusammen und teilst sie durch die Anzahl der Personen: (1+1+2+4+5)/5 = 2,6.
Das ging dir zu schnell? Kein Problem. Schau dir Mittelwert, Median und Modus jetzt in Ruhe der Reihe nach an.
Der Modus
Der Modus (auch: Modalwert) ist der Wert, der in den Daten am häufigsten vorkommt. Du kannst den Modus nicht berechnen, aber ablesen:
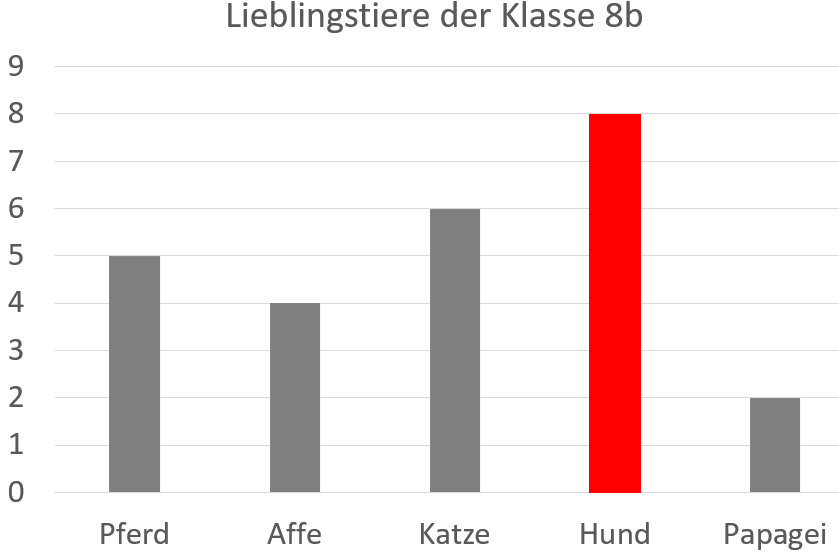
- Im Säulendiagramm
ist der Modus immer das Merkmal mit der höchsten Säule, hier also Hund.
Modus am Balkendiagramm - In der Tabelle ist der Modus das Merkmal mit der höchsten Anzahl.
Pferd Affe Katze Hund Papagei 5 4 6 8 2
Natürlich können auch mehrere Merkmale gleich oft vorkommen. Dann gibt es mehrere Modi.
📈 Wann verwendest du den Modus? In Mathe ist der Modus besonders wichtig, wenn du die gegebenen Kategorien nicht ordnen kannst (z.B. Lieblingstier, Beruf, Geschlecht, …). Der Modus ist dann meist das Einzige, was sich überhaupt bestimmen lässt. Viele andere Berechnungen funktionieren nämlich nur, wenn du die Merkmale ordnen kannst (z.B. Noten, Körpergröße, Alter, …).
Median
Angenommen, du sortierst deine Daten der Größe nach. Dann liegt der Median (auch: Zentralwert ) in der Mitte. Die Hälfte der Daten liegt also unter dem Median und die andere Hälfte darüber.
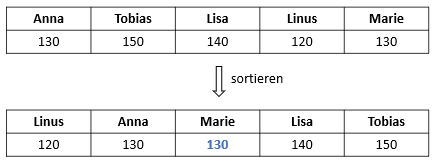
Um den Median zu ermitteln, unterscheidest du zwei Fälle. Schau sie dir am Beispiel der Körpergrößen einer Freundesgruppe an.
Gerade Anzahl an Daten
- Sortiere die Daten der Größe nach.
- Es gibt hier keinen eindeutigen Wert in der Mitte, sondern zwei:
Die beiden mittleren Werte rechnest du zusammen und teilst das Ergebnis durch 2.
(130 + 140) : 2 = 135
Die Median-Körpergröße liegt also bei 135 cm.
📈 Wann verwendest du den Median? Um den Median zu bestimmen, müssen sich deine Daten natürlich ordnen lassen. Das gilt z.B. für Noten, Körpergröße oder Alter, aber nicht für das Lieblingstier.
Der Median von Daten gibt an wie groß oder klein ein bestimmter Wert im Vergleich zu den anderen Werten einer Datenreihe ist. Liegt deine Körpergröße z.B. über der Median-Körpergröße, bist du eher groß. Liegt sie darunter, eher klein.
Mittelwert
Der Mittelwert (auch: arithmetisches Mittel ) ist der Durchschnitt der Daten. Schau dir die Berechnung am Beispiel an. Hier siehst du das Taschengeld von 5 Schülern:
| Anna | Tobias | Lisa | Linus | Marie |
| 5 € | 10 € | 8 € | 5 € | 2 € |
- Rechne alle Daten zusammen: 5 + 10 + 8 + 5 + 2 = 30
-
Teile das Ergebnis durch die Anzahl der Daten (hier: 5):
30 : 5 = 6
Durchschnittlich bekommen die Schüler also 6 € Taschengeld.
📈 Wann verwendest du den Mittelwert? Um den Mittelwert zu berechnen, müssen deine Daten Zahlen sein. Das gilt z.B. für Noten und Körpergrößen, aber nicht für Bewertungen (z.B. „gut“, „mittel“, „schlecht“) oder das Lieblingstier.
Vergleich von Modus, Median und Mittelwert
Der Modus eignet sich in der Statistik vor allem für Daten, die du nicht ordnen kannst. Sind deine Daten aber Zahlen (→ sie lassen sich also ordnen), kannst du Median und Durchschnitt bestimmen. Schau dir die beiden Lagemaße im Vergleich an.
Hier siehst du die Höhe des Taschengeldes von 5 Personen. Du kannst den Median und das arithmetische Mittel bestimmen.
| Linus | Anna | Marie | Laura | Paul |
| 5 € | 5 € | 6 € | 8 € | 50 € |
Median vs. Mittelwert
- Der Median ist der Wert in der Mitte, also 6 €.
- Der Mittelwert der Beträge ist aber:
Er ist viel größer als der Median, weil er von einem „Ausreißer“ nach oben gezogen wird. Weil eine Person (Paul) viel mehr Taschengeld bekommt als die anderen, ist also auch der Mittelwert groß.![Rendered by QuickLaTeX.com \[\frac{5+5+6+8+50}{5} = \textcolor{olive}{14,80 \text{€}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b97592fde59a118de4ce7b8e7cf5cf71_l3.png)
Merke: Der Median ist unempfindlicher gegenüber Ausreißern als der Mittelwert. Er macht deshalb eine bessere Aussage darüber, wie groß oder klein ein Wert im Vergleich zu den anderen Werten ist. Bekommst du zum Beispiel 12 Euro Taschengeld, dann ist das im Vergleich zu der Freundesgruppe eher viel (4 Personen bekommen ja weniger!), aber trotzdem liegt dein Taschengeld unter dem Mittelwert (weil Paul eben extrem viel bekommt).
Mittelwert, Median, Modus — häufigste Fragen
-
Wann Modus Median Mittelwert?
Der Modus ist das einfachste Lagemaß: Er ist einfach der Wert in deiner Stichprobe, der am häufigsten vorkommt. Der Median teilt deine Messwerte hingegen in zwei gleich große Hälften. Er ist also der Wert, der genau in der Mitte liegt, wenn du deine Messwerte in eine aufsteigende Rangreihe bringst. Der Mittewert ist einfach der Durchschnitt aller Werte.
-
Was ist der Unterschied zwischen Mittelwert und Median?
Du berechnest den Mittelwert, indem du alle Werte addierst und das Ergebnis durch die Anzahl der Werte teilst. Beispiel: (2+1+6)/3 = 3. Der Median dagegen ist der Wert genau in der Mitte, wenn du die Werte in aufsteigender Reihenfolge sortierst. Beispiel: 1, 2 und 6 → Median: 2
-
Was ist der Modus in Statistik?
Der Modus (auch: Modalwert) ist der Wert, der in einer Datenreihe am häufigsten vorkommt. Kommen mehrere Werte am häufigsten vor (z.B. alle 5 Mal), gibt es mehrere Modi.
-
Wie kann man den Modus berechnen?
Du kannst den Modus ganz einfach berechnen: Schau dir die Häufigkeiten der einzelnen Daten an. Der Modus ist einfach der Wert, der am öftesten vorkommt (häufigster Beobachtungswert). Du kürzt ihn mit x̄d ab.
Mittelwert berechnen
Super! Jetzt hast du einen guten Überblick über Durchschnitt, Median und Modus in der Statistik. Du möchtest noch genauer wissen, wie du den Mittelwert berechnest? Dann schau doch mal hier vorbei!