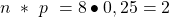Quantile
Dieser Artikel liefert dir eine Definition was Quantile in der Statistik sind und wie man Quantile berechnen kann.
Du hast genug von trockener Theorie in Textform? Unser Video zum Thema Quantil erklärt dir alles, was du wissen musst im Handumdrehen!
Quantil Definition
Quantile gehören zu den Lagemaßen der Statistik. Sie teilen eine bestimmte Menge an Daten so ein, dass ein Teil p kleiner oder gleich und der andere Teil 1-p größer oder gleich dem Quantil ist. Das 20%-Quantil oder auch 0.2-Quantil zum Beispiel sagt aus, dass genau 20 Prozent der Werte einer Verteilung unter dem Quantil liegen. Der Rest der Werte liegt darüber.
Quantile Statistik
Du fragst dich wofür man so ein Lagemaß überhaupt braucht? Quantile sind sehr praktisch um Aussagen, wie: „20 Prozent der Studenten haben eine bessere Bachelornote als 1,8“, zu treffen. 1,8 wäre hier das 20%-Quantil.
Quantile bestimmen
Manche Quantile sind in der Statistik so wichtig, dass sie einen eigenen Namen bekommen haben. So ist das 50%-Quantil nichts anderes als der Median. Ist ja auch logisch. Er teilt die Verteilung genau in der Mitte. Quintile, Dezile und Perzile sind andere Einteilungen, welche die Verteilung in 5, 10 bzw. 100 gleichgroße Teile splitten. Oft werden diese speziellen Quantile nur mit diesen Begriffen bezeichnet.
Quartile
Am öftesten werden jedoch die Quartile verwerndet. Sie unterteilen die Verteilung in vier gleich große Teile. Es gibt also das 0,25-Quantil, das 0,5-Quantil oder eben auch Median genannt und das 0,75-Quantil. Quartile sind in der Statistik die am häufigsten verwendete Form der Quantile.
Quantile berechnen
Nun wollen wir einmal selbst Quantile anhand eines Beispiels berechnen. Angenommen wir haben zwei Verteilungen:
Für diese wollen wir das 25%-Quantil berechnen. Wir unterscheiden dabei zwischen zwei Formeln: eine, falls n mal p ganzzahlig ist und die andere, falls n mal p nicht ganzzahlig ist:
np ganzzahlig
np nicht ganzzahlig
Quantil berechnen: Verteilung ganzzahlig
Beginnen wir mit der ersten Verteilung. Hier ist n mal p gleich 2 und somit ganzzahlig.
Wir rechnen:
Das erste Quartil von der Verteilung ist 2,5. Das bedeutet, dass 25 Prozent der Werte kleiner als 2,5 sind.
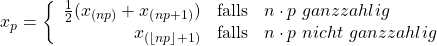
Quantil berechnen: Verteilung nicht ganzzahlig
Die zweite Verteilung gestaltet sich schon ein bisschen komplizierter. N mal p ist hier nämlich nicht ganzzahlig, weshalb wir die andere Formel verwenden müssen.
Die Klammer im Index bedeutet, dass wir den Wert zwischen der Klammer immer abrunden, egal wie nah er am nächsthöherem Wert liegt. Mit diesem Wissen ist die Berechnung aber sehr einfach und du kommst auf folgendes Ergebnis:
$x_{0,25}=x_{(\left\lfloor1,75\right\rfloor+1)}=x_{1+1}=1$
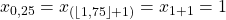
Das erste Quartil ist hier also 1.
Super! Jetzt kennst du die verschiedenen Bezeichnungen von Quantilen und weißt, wie man sie berechnet. Achte immer darauf, die richtige Formel zu benutzen, um auf ein richtiges Ergebnis zu kommen.
