Mittelwert
Du willst wissen, was der Mittelwert in der Statistik ist und wie du ihn berechnest? Dann ist dieser Artikel und unser Video genau das Richtige für dich!
Inhaltsübersicht
Mittelwert Definition
Der Mittelwert ist ein sogenanntes Lagemaß aus der deskriptiven (beschreibenden) Statistik . Lagemaße geben Eigenschaften einer Datenmenge an und helfen so, einen Überblick über die Daten zu bekommen.
Der Mittelwert 
beschreibt den Durchschnitt einer Datenmenge, also das arithmetische Mittel aller Datenpunkte. Du ermittelst ihn, indem du die Summe der Datenpunkte durch die Anzahl der Datenpunkte teilst:
![\[\bar{x} = \frac{\text{Summe der Datenpunkte}}{\text{Anzahl der Datenpunkte}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9706437755641feb3d264dc8abfde10f_l3.png "Rendered by QuickLaTeX.com")
Mittelwert Beispiel
Bei einer kleinen Studie mit 10 Teilnehmern wurde unter anderem das Alter der Personen notiert. Daraus ergab sich folgende Datenmenge:
| 22 Jahre | 19 Jahre | 25 Jahre | 23 Jahre | 18 Jahre | 42 Jahre | 40 Jahre | 24 Jahre | 23 Jahre | 19 Jahre |
Der Mittelwert macht jetzt eine Aussage über das durchschnittliche Alter der Personen. Er liegt hier bei:
![\[\bar{x} = \frac{22+19+25+23+18+42+40+24+23+19}{\textcolor{blue}{10}} = 22,5\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2ea9d3e74a2e752497569108b9a8aa8b_l3.png "Rendered by QuickLaTeX.com")
Die Teilnehmer sind also durchschnittlich 22,5 Jahre alt.
Achtung! Bei der Interpretation dieser Zahl ist Vorsicht geboten! Sie macht lediglich eine Aussage über den Durchschnitt, aber nicht über die Verteilung der Daten. Im Beispiel erfasst sie etwa nicht, dass zwei der Teilnehmer deutlich älter waren als der Rest.
Aufgrund seiner Definition ist der Mittelwert zudem sehr empfindlich gegenüber Ausreißern. Wenn einige Werte deutlich größer sind als andere, können sie das Ergebnis verfälschen. Der Median macht dann oft eine bessere Aussage.
Mittelwert aus absoluten Häufigkeiten berechnen
Manchmal kennst du nicht die einzelnen Datenpunkte, sondern nur eine Häufigkeitsverteilung. Eine absolute Häufigkeitsverteilung gibt an, wie oft ein bestimmter Wert beobachtet wurde.
Um den Mittelwert zu berechnen , multiplizierst du die Werte mit ihrer jeweiligen Häufigkeit und teilst das Ergebnis durch die Summe der Häufigkeiten:
![\[\bar{x} = \frac{\textcolor{orange}{x_1} \cdot \textcolor{teal}{H_1}+\textcolor{orange}{x_2} \cdot \textcolor{teal}{H_2} + \dots +\textcolor{orange}{x_n} \cdot \textcolor{teal}{H_n}}{\textcolor{teal}{H_1}+\textcolor{teal}{H_2}+\dots + \textcolor{teal}{H_n}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dcd197d3723f0b255f3aae3ef2137a0e_l3.png "Rendered by QuickLaTeX.com")
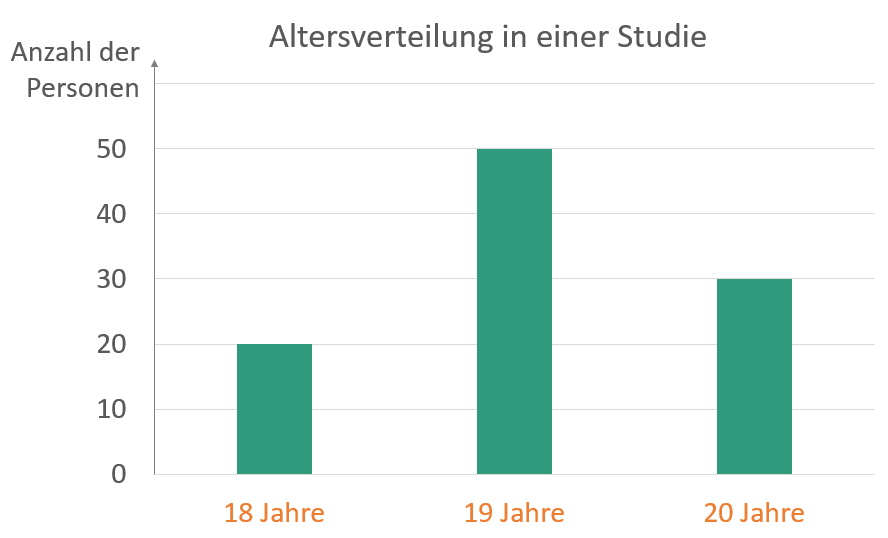
Beispiel: In einer Studie wurden 100 Leute zwischen 18 und 20 Jahren befragt. Die Altersverteilung ist in folgendem Diagramm dargestellt:
Als statistischer Mittelwert ergibt sich:
![\[\bar{x} = \frac{\textcolor{orange}{18} \cdot \textcolor{teal}{20} +\textcolor{orange}{19} \cdot \textcolor{teal}{50} +\textcolor{orange}{20} \cdot \textcolor{teal}{30}}{\textcolor{teal}{20}+\textcolor{teal}{50}+\textcolor{teal}{30}} = 19,1\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e5053910e5edc1e4e5f88164e8b8d52b_l3.png "Rendered by QuickLaTeX.com")
Das Durchschnittsalter liegt also bei 19,1 Jahren.
Übrigens: Auch bei Notendurchschnitten in der Schule oder an der Uni wird der Mittelwert mit absoluten Häufigkeiten verwendet.
Mittelwert aus relativen Häufigkeiten berechnen
Eine relative Häufigkeitsverteilung gibt an, welchen Anteil ein Datenpunkt in der gesamten Datenmenge ausmacht. Auch aus relativen Häufigkeiten kannst du einen Mittelwert berechnen.
Er ergibt sich, wenn du die einzelnen Werte mit den jeweiligen relativen Häufigkeiten multiplizierst und die Ergebnisse addierst:
![\[\bar{x} = \textcolor{orange}{x_1} \cdot \textcolor{olive}{h_1} + \textcolor{orange}{x_2}\cdot \textcolor{olive}{h_2} + \dots + \textcolor{orange}{x_n} \cdot \textcolor{olive}{h_n}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-effca1d102de886c21e665f36058bc1c_l3.png "Rendered by QuickLaTeX.com")
Beispiel: Die Altersverteilung aus der Studie des vorherigen Beispiels ist nun in einem Kreisdiagramm dargestellt. Es gibt die relativen Häufigkeiten an, also welcher Anteil der Personen einer bestimmten Altersgruppe angehört.
Um damit den Mittelwert zu berechnen, wandelst du die Prozentzahlen zunächst in Dezimalzahlen um. Du erhältst als arithmetisches Mittel :
![\[\bar{x} = \textcolor{orange}{18} \cdot \textcolor{olive}{20\%} + \textcolor{orange}{19}\cdot \textcolor{olive}{50\%} + \textcolor{orange}{20}\cdot \textcolor{olive}{30\%} = \textcolor{orange}{18} \cdot \textcolor{olive}{0,2} + \textcolor{orange}{19}\cdot \textcolor{olive}{0,5} + \textcolor{orange}{20}\cdot \textcolor{olive}{0,3} = 19,1\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-35033245739d63378e024f6d87c0cad0_l3.png "Rendered by QuickLaTeX.com")
Gewichteter Mittelwert
Der gewichtete Mittelwert kommt dann zum Einsatz, wenn einige Datenpunkte ein höheres Gewicht bekommen sollen als andere.
Um ihn zu berechnen, multiplizierst du jeden Datenpunkt mit seinem Gewicht und teilst das Ergebnis durch die Summe der Gewichte:
![\[\bar{x}_{\text{g}} = \frac{\textcolor{purple}{g_1} \cdot \textcolor{orange}{x_1} + \textcolor{purple}{g_2} \cdot \textcolor{orange}{x_2} + \dots + \textcolor{purple}{g_n} \cdot \textcolor{orange}{x_n}}{\textcolor{purple}{g_1} + \textcolor{purple}{g_2} + \dots \textcolor{purple}{g_n}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ec310b05531ca8826cf0383b2a1a6a60_l3.png "Rendered by QuickLaTeX.com")
Beispiel: In einer Studie soll erfasst werden, wie viel Geld die Bewohner in den Städten A, B und C monatlich für Freizeitaktivitäten ausgeben. Hierfür gibt es folgende Daten:
| Stadt | Stadt A | Stadt B | Stadt C |
| Einwohnerzahl | 20.000 | 30.000 | 100.000 |
| Ausgaben pro Kopf | 100 € | 120 € | 70 € |
Ein „normaler” statistischer Mittelwert aus den Zahlen 100, 120 und 70 ist hier nicht sinnvoll, weil die Städte unterschiedlich viele Einwohner haben. Um das zu berücksichtigen, werden die Ausgaben pro Kopf mit der Einwohnerzahl gewichtet:
![\[\bar{x}_{\text{g}} = \frac{\textcolor{purple}{20000} \cdot \textcolor{orange}{100 €} + \textcolor{purple}{30000} \cdot \textcolor{orange}{120 €} + \textcolor{purple}{100000} \cdot \textcolor{orange}{70 €}}{\textcolor{purple}{20000}+\textcolor{purple}{30000}+\textcolor{purple}{100000}} = 84 €\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dfee5b01dfea3652c7f333c931f86d1b_l3.png "Rendered by QuickLaTeX.com")
Die durchschnittlichen Ausgaben liegen also bei 84 €.
Gleitender Mittelwert
Der gleitende Mittelwert berechnet statistische Mittelwerte im Verlauf der Zeit.
Beispiel: Die blaue Kurve stellt den Umsatz eines Unternehmens in jedem Monat dar. Die rote Kurve zeigt den gleitenden Mittelwert: Jeder Datenpunkt in der roten Kurve ist der Mittelwert aus den drei vorherigen Monaten. Der Datenpunkt im Februar ist beispielsweise der Mittelwert aus den Umsätzen im Januar, Februar und März.
Der gleitende Durchschnitt gleicht die extremen Ausschläge in der blauen Kurve aus und glättet so den Verlauf.
Mittelwert — häufigste Fragen
-
Was ist der Mittelwert in der Statistik?
Der Mittelwert in der Statistik gehört zu den Lageparametern. Er beschreibt den statistischen Durchschnitt einer Datenmenge. Um ihn zu berechnen, addiert man alle Datenpunkte und teilt das Ergebnis durch die Anzahl der Werte.
-
Ist der Mittelwert auch der Durchschnitt?
Der Mittelwert (auch: arithmetisches Mittel) wird im Alltag oft als Durchschnitt bezeichnet. Du erhältst ihn, indem du die alle Datenpunkte zusammenrechnest und das Ergebnis durch die Anzahl der Datenpunkte teilst.
-
Warum braucht man den Mittelwert?
Mit dem Mittelwert kannst du zum Beispiel berechnen, wie viel die Menschen in einem Land durchschnittlich verdienen oder wie groß sie durchschnittlich sind. Die Ergebnisse kannst du dann mit anderen Ländern vergleichen.
Mittelwert, Median, Modus
Neben dem eigentlichen Mittelwert gibt es noch andere statistische Mittelwerte bzw. Lageparameter. Besonders wichtig sind der Median und der Modus (auch Modalwert):
- Der Median beschreibt die Mitte einer geordneten Datenreihe. Er teilt die Daten in eine obere und eine untere Hälfte. Anders als der Mittelwert wird er nicht so stark von extremen Werten („Ausreißern”) beeinflusst.
- Der Modus gibt an, welcher Wert in einer Datenmenge am häufigsten auftritt.
Du möchtest dir die einzelnen Lageparameter im Vergleich anschauen? Dann ist dieser Artikel genau das Richtige für dich!
