Video anzeigen

Einfaktorielle Varianzanalyse

In diesem Artikel zeigen wir dir die einfaktorielle Varianzanalyse. Wir erklären dir, worum es bei der einfaktoriellen Varianzanalyse geht und rechnen gemeinsam ein Beispiel durch.

Du willst lieber hören statt lesen? Dann schau dir doch direkt unser Video zum Thema an!

Inhaltsübersicht

Einfaktorielle Varianzanalyse einfach erklärt

Mit der einfaktoriellen Varianzanalyse kannst du testen, ob sich die Mittelwerte von mehreren Gruppen voneinander unterscheiden. Das Ziel ist also ähnlich wie das des t-Tests . Jedoch kannst du mit Varianzanalyse nicht nur zwei, sondern beliebig viele Mittelwerte gleichzeitig miteinander vergleichen. Bei der Varianzanalyse überprüfst du, ob ein Teil der Varianz der Messwerte der abhängigen Variable dadurch entsteht, dass Personen unterschiedlichen Gruppen angehören. Ist das der Fall, darfst du davon ausgehen, dass sich die Mittelwerte der einzelnen Gruppen statistisch signifikant unterscheiden. Wenn du die Grundidee der einfaktoriellen Varianzanalyse noch genauer verstehen möchtest, dann schau gerne in diesem Beitrag hier vorbei.

Das klingt immer noch ein wenig abstrakt, nicht wahr? Schauen wir uns die einfaktorielle Varianzanalyse also direkt an einem Beispiel an.

Einfaktorielle Varianzanalyse: Beispiel

Legen wir gleich mit einem Rechenbeispiel zur einfaktoriellen Varianzanalyse los:

Varianzanalyse, Faktor, Statistik, allgemeines lineares Modell, einfaktoriell, Gruppen, Varianz — Beispiel: Einfaktorielle Varianzanalyse

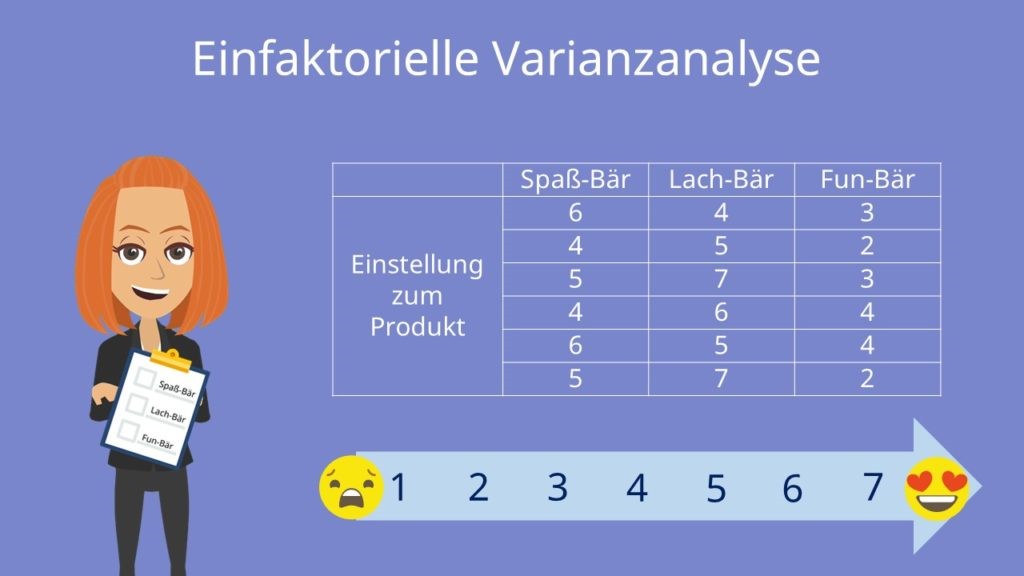
Im Rahmen deines Praktikums bei einem Gummibärenhersteller sollst du eine Studie zu potentiellen Namen für eine neue Gummibärchensorte durchführen. Dazu bewerten sechs Personen die drei möglichen Namen auf einer siebenstufigen Ratingskala. Eins entspricht dabei „überhaupt nicht attraktiv“, sieben bedeutet „sehr attraktiv“. Die Einstellung der Personen zum Produkt siehst du in folgender Tabelle:

einfaktorielle Varianzanalyse, Beispielrechnung, Gruppenmittelwerte, Ratingskala, Einstellungsforschung — Tabelle mit Messwerten

Nun will dein Abteilungsleiter von dir wissen, ob mit einer Irrtumswahrscheinlichkeit von $\alpha = 5 \%$ davon ausgegangen werden kann, dass sich das mittlere Einstellungsrating zwischen den drei möglichen Namen unterschiedet. Um das zu testen, musst du eine einfaktorielle Varianzanalyse durchführen.

Prüfung der Voraussetzungen

Da dein Chef ein Perfektionist ist, erwartet er von dir, dass du vor der Varianzanalyse die nötigen Voraussetzungen prüfst. Dazu gehört unter anderem, dass du die Normalverteilung der abhängigen Variable, sowie die Varianzhomogenität sicherstellst.

Zudem muss die abhängige Variable intervallskaliert und die unabhängige Variable nominalskaliert sein. Die abhängige Variable in unserem Beispiel ist das Einstellungsranking, das auf einer siebenstufigen Skala erfasst wurde. Für unsere Berechnungen sehen wir diese Skala als intervallskaliert mit gleichen Abständen zwischen den einzelnen Stufen an. Die unabhängige Variable, der Name der Gummibärchensorte, weist ein nominales Skalenniveau auf. Schließlich hat die Variable nur drei Ausprägungen, die man nicht in eine logisch aufsteigende Rangreihe bringen kann.

Test auf Varianzhomogenität

Die Normalverteilung der abhängigen Variable nehmen wir als gegeben an. Die Varianzhomogenität müssen wir aber testen. Bei der Varianzhomogenität geht es darum, dass die Varianz in allen untersuchten Gruppen gleich sein soll. Die Rankings für den Namen „Spaß-Bär“ sollen also nicht alle viel weiter auseinander liegen als die Rankings für „Lach-Bär“ oder „Fun-Bär“. Das mittlere Ranking darf sich dabei durchaus unterscheiden, bei der Varianzhomogenität geht es lediglich darum, dass die Varianz in allen drei Gruppen gleich ist.

Dabei testen wir stets auf Abweichung von Varianzhomogenität. Ist der Test also nicht signifikant, können wir von Varianzhomogenität ausgehen, ist er hingegen signifikant, ist die Annahme verletzt. Somit lautet die Alternativhypothese :

$\sigma^2_{Spaß-Bär} \neq \sigma^2_{Lach-Bär} \neq \sigma^2_{Fun-Bär}$

Die Nullhypothese lautet hingegen:

$\sigma^2_{Spaß-Bär} = \sigma^2_{Lach-Bär} = \sigma^2_{Fun-Bär}$

Test auf Varianzhomogenität: Vorbereitung

Damit wir auf Varianzhomogenität testen können, müssen wir damit, die Stichprobenvarianzen in den einzelnen Gruppen zu ermitteln Dafür berechnen wir zuerst den Mittelwert der Einstellung der drei Gruppen.

$\bar {x}_{Spaß-Bär} = 5$
$\bar {x}_{Lachbär-Bär} = 5,67$
$\bar {x}_{Fun-Bär} = 3$

Jetzt können wir alle unsere Werte in die Formel der Stichprobenvarianz einsetzen. Die Anzahl an Beobachtungen beträgt 6. Damit erhalten wir:

$s^2_{Spaß-Bär} = 0,8$
$s^2_{Fun-Bär} = 1,47$
$s^2_{Lach-Bär} = 0,8$

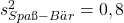
Wenn du nochmal wiederholen möchtest, wie man die Varianz genau berechnet, dann schau in diesem Beitrag vorbei.

Varianz, Varianzhomogenität, Test, Beispiel, Voraussetzungen prüfen, Varianzanalyse — Stichprobenvarianzen berechnen

Test auf Varianzhomogenität: Durchführung

Nun können wir auf Varianzhomogenität prüfen. Die Formel für den Test lautet:

$C = \frac {max s^2_i} {\sum s^2_i}$

In den Zähler des Bruchs müssen wir die größte unserer Varianzen einsetzen. In unserm Beispiel ist das $s^2_{Fun-Bär} = 1,47$ . Der Nenner ist einfach die Summe der drei Stichprobenvarianzen. Rechnest du die Summe aus erhältst du 3,07.

$C = \frac {1,47} {3,07}$

Das musst du jetzt nur noch ausrechnen und du erhältst einen C-Wert von 0,479.

$C = \frac {1,47} {3,07} = 0,479$

Um jetzt die Hypothese, dass die Varianzen gleich sind, zu überprüfen, benötigen wir noch den kritischen Bereich. Den kritischen Bereich können wir aus der Formelsammlung ablesen. Wir erhalten, dass er bei (0,7071;1) beginnt. Unser C-Wert liegt nicht im kritischen Bereich.

Somit kann die Nullhypothese nicht verworfen werden und wir können von Varianzhomogenität ausgehen.

Voraussetzungen, Homoskedastizität. Hetereoskedastizität, Varianzanalyse — Test auf Varianzhomogenität

Forschungshypothese

Super! Jetzt haben wir alle notwendigen Voraussetzungen für die einfaktorielle Varianzanalyse getestet und können mit der Berechnung starten.

Unsere Forschungshypothese für die Varianzanalyse lautet: Nicht alle Gruppenmittelwerte sind gleich beziehungsweise mindestens einer der Mittelwerte unterscheidet sich von den anderen.

F-Test: Formel

Um die einfaktorielle Varianzanalyse durchzuführen, brauchen wir folgende Formel:

$F_{ber} = \frac {MQA}{MQR}$

wobei:

$MQA = \frac {\sum n_ i \times ( \bar{x_i} - \bar {x})^2} {I-1}$

und:

$MQR = \frac { \sum \sum (x_{ij} - \bar x_i)^2} {N-I}$

Wenn du möchtest, kannst du die Formeln für MQA und MQR auch direkt in den F-Bruch der einfaktoriellen Varianzanalyse einsetzen und alles zusammen ausrechnen. Achte hierbei jedoch darauf, dass du beim Aufsummieren nichts vergisst, da der Bruch schnell unübersichtlich werden kann.

Varianzanalyse, F-Bruch, Alternativhypothese, Test — Forschungshypothese und Berechnung der MQA

Berechnung MQA und MQR

Die Formel der einfaktoriellen Varianzanalyse sieht erstmal kompliziert aus. Lass uns deshalb Schritt für Schritt vorgehen. Fangen wir beim Zähler des Bruchs (MQA) an:

$MQA = \frac {\sum n_ i \times ( \bar{x_i} - \bar {x})^2} {I-1}$

Dieser ist relativ einfach zu berechnen, da wir die Gruppenmittelwerte $\bar {x_i}$ bereits bei der Überprüfung der Varianzhomogenität berechnet haben. Somit fehlt uns für die Berechnung nur noch der Gesamtmittelwert über alle Gruppen hinweg $\bar x$ . Um diesen zu erhalten, addieren wir die drei Gruppenmittelwerte 5, 5,67 und 3. Dann teilen wir durch 3 und erhalten den Wert 4,56.

$\bar x = \frac {\sum \bar x_i} {I} = \frac {5+5,67+3}{3} = 4,56$

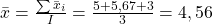
Vorsicht! Wenn nicht in allen Gruppen gleich viele Personen sind, musst du den Gesamtmittelwert berechnen, indem du alle Messwerte aufsummierst und durch die Gesamtanzahl der Personen teilst.

Jetzt haben wir alle notwendigen Werte für die MQA und können diese einsetzen.

$MQA = \frac {\sum n_ i \times ( \bar{x_i} - \bar {x})^2} {I-1} = \frac {6 \times (5-4,56)^2 + 6 \times (5,67 - 4,56)^2 + 6 \times (3-4,56)^2}{3-1} = 11,58$

Nun widmen wir uns dem Nenner (MQR).

$MQR = \frac { \sum \sum (x_{ij} - \bar x_i)^2} {N-I}$

Dafür müssen wir noch $\sum \sum (x_{ij} - \bar x_i)^2$ berechnen. Dafür ziehen wir von jedem einzelnen Messwert der Einstellung den Mittelwert des zugehörigen Sortennamens ab und quadrierst das Ergebnis. Du betrachtest also etwa, wie Person 1 den Spaß-Bär bewertet hat und ziehst von diesem Messwert den Mittelwert von Spaß-Bär ab. Das Ergebnis der Differenz quadrierst du anschließend.

Beispiel: $(x_{ij} - \bar x_i)^2 = (x_{Spaß-Bär, 1} - \bar x_{Spaß-Bär} =(6 - 5)^2 = 1$

Diesen Vorgang musst du für alle übrigen Personen und für die anderen beiden Sortennamen wiederholen. Anschließend müssen wir die einzelnen Werte aufsummieren.

$\sum \sum (x_{ij} - \bar x_i)^2 = 15,34$

Als Ergebnis erhältst du den Wert 15,34. Diesen müssen wir nun noch durch N-I teilen, um den Wert des Nenners MQR zu erhalten. Bei musst du aufpassen, da es sich diesmal nicht um die Anzahl an Befragungen einer einzelnen Sorte handelt, sondern um die Gesamtanzahl der Messwerte, also: 6 mal 3 gleich 18.

$MQR = \frac {15,34} {N-I} = \frac {15,34}{18-3} = \frac{15,34}{15} = 1,023$

Nun haben wir auch alle Werte für den Nenner.

Durchführung des F-Tests und Testentscheidung

Die erhaltenen Werte setzen wir nun in unseren F-Bruch ein.

$F_{ber} = \frac {MQA}{MQR} = \frac {11,58}{1,023} = 11,32$

Der berechnete F-Wert beträgt folglich 11,32. Zur Überprüfung der Hypothese benötigen wir nun noch den kritischen Wert beziehungsweise den kritischen Bereich.

Den kritischen Wert schlägst du in der F-Verteilungstabelle nach. Dabei musst du darauf achten, die richtige Anzahl an Freiheitsgraden und das richtige Signifikanzniveau $\alpha$ zu verwenden.
Die Freiheitsgrade berechnest du folgendermaßen:

$\nu_1 = I -1$
$\nu_2 = N - I$

Für das Signifikanzniveau $\alpha$ hatten du und dein Chef $\alpha = 5\%$ gewählt. Bei einer einfaktoriellen Varianzanalyse testet man immer einseitig nach oben. Deshalb schlägst du in der Tabelle stets für $1- \alpha$ nach. Mit diesen Informationen schlagen wir in der Tabelle nach und erhalten den kritischen Wert $F_{krit}=3,68$ . Somit lautet der kritische Bereich (3,68; ∞) (von 3,68 bis unendlich).

Wir sehen, dass unser berechneter F-Wert Teil des kritischen Bereichs ist. Somit kann die H_0 -Hypothese verworfen und die Alternativhypothese H_1 vorläufig angenommen werden. Es liegt also ein signifikantes Ergebnis vor und du darfst davon ausgehen, dass es Unterschiede zwischen den mittleren Einstellungsratings der drei möglichen Sortennamen gibt.

Post-hoc Tests

Was du jedoch nicht weißt, ist, zwischen welchen Sortennamen ein Unterschied besteht. Wenn du das auch noch herausfinden möchtest, musst du im Anschluss an die einfaktorielle Varianzanalyse noch sogenannte Post-Hoc-Tests rechnen. Mit ihrer Hilfe kannst du bestimmen, welche der drei Gruppen sich genau signifikant unterscheiden.

Beliebte Inhalte aus dem Bereich Marketing

Primärforschung

Sekundärforschung

Einfaktorielle Varianzanalyse

Conjoint-Analyse

Marktsegmentierung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .