Normalverteilung
Du willst wissen, wie du die Normalverteilung berechnen und zur Standardnormalverteilung transformieren kannst? Alles über die Gaußsche Normalverteilung erfährst du in unserem Beitrag und in unserem Video! Viel Spaß!
Inhaltsübersicht
Normalverteilung einfach erklärt
Die Normalverteilung verwendest du, um Häufigkeiten von Daten und Beobachtungen darzustellen. Du nennst die Normalverteilung auch Gaußverteilung (nach dem deutschen Mathematiker Carl Friedrich Gauß) oder Glockenkurve — entsprechend dem typischen Verlauf der Normalverteilung.
![Rendered by QuickLaTeX.com \[f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\cdot {(\frac{x-\mu}{\sigma}})^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ab1f0b53fafc3549c3f2246aac58a52f_l3.png)
- mit der Zufallsgröße x
- dem Erwartungswert μ
- und der Varianz σ² (bzw. der aus √σ² resultierenden Standardabweichung σ)
Normalverteilung Statistik
Aber warum ist die Gaußsche Normalverteilung denn nun die wichtigste Verteilung in der Statistik? Ganz einfach: so gut wie jeder Mittelwert einer x-beliebigen stetigen Verteilung folgt der Glockenkurve. Diese Besonderheit ist auch als zentraler Grenzwertsatz bekannt.
So ist zum Beispiel die Körpergröße der Menschen annähernd normalverteilt. Das liegt daran, dass es nun mal wenig Zwerge und Riesen unter den Menschen gibt. Dafür aber ziemlich viele Personen, welche annähernd so groß sind wie der Durchschnitt. Somit ergibt sich auch die charakteristische glockenförmige Gaußverteilung.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Normalverteilung Formel
Die Formeln und Variablen für die Gauß Verteilung sind nicht sehr kompliziert. Du musst jedoch darauf achten, die richtigen Werte an der richtigen Stelle einzusetzen. Die Gaußsche Normalverteilung hängt grundsätzlich von zwei Kennzahlen ab: dem Erwartungswert μ und der Varianz σ², wobei gilt:
 und
und 
Die Gaussverteilung bezeichnest du deswegen auch kurz als N(μ,σ²).
Außerdem ist es wichtig zu wissen, dass du bei manchen Aufgaben zur Gauss Verteilung zuerst die Standardnormalverteilung berechnen musst.
Klasse! Jetzt kennst du schon die Normalverteilung Formel!
Gaußsche Normalverteilung: Erwartungswert und Varianz
Veränderst du den Erwartungswert μ, verschiebt sich die Kurve nach links oder rechts. Das ist auch logisch, denn bei μ liegt immer das Maximum. Das liegt daran, dass der erwartete Wert in einer Stichprobe am häufigsten vorkommt. Je größer der Erwartungswert μ, desto weiter verschiebt sich die Funktion auf der x- Achse nach rechts.
Die Varianz σ² hingegen verändert die Form deiner Glockenkurve, sie wird also entweder gestreckt oder gestaucht. Je größer dein Sigma, desto gestauchter wird die Funktion: Die Gaussche Normalverteilung wird also breiter.
Dichtefunktion Normalverteilung
Die Dichtefunktion normalverteilter Werte sieht auf den ersten Blick vielleicht schwierig aus, besteht aber im Endeffekt nur aus den bereits behandelten Variablen.
![Rendered by QuickLaTeX.com \[f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\cdot {(\frac{x-\mu}{\sigma}})^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ab1f0b53fafc3549c3f2246aac58a52f_l3.png)
Eine Dichtefunktion der Gauss Normalverteilung mit N(μ,σ²) hat dabei folgende Eigenschaften:
Sie…
- besteht aus dem Erwartungswert μ und der Standardabweichung σ
- ist symmetrisch zur Symmetrieachse y= μ
- ist nie 0
- ist unimodal (eingipflig)
- erreicht ihr Maximum am Erwartungswert μ
- ist bei ihrer Ableitung positiv für Werte von x < µ und negativ für Werte von x > µ
- ist stetig und daher von -∞ bis ∞ definiert
- hat zwei Wendestellen: Diese sind genau eine Standardabweichung vom Erwartungswert entfernt, nämlich bei x1 = µ – σ und x2 = µ + σ
In dieser Graphik erkennst du die Lage annähernd normalverteilter Daten: 68% aller Daten befinden sich innerhalb einer Standardabweichung vom Erwartungswert. 95% liegen innerhalb von 2 Standardabweichungen vom Erwartungswert. Und fast alle Daten, nämlich 99,7% befinden sich innerhalb von 3 Standardabweichungen vom Erwartungswert. Um dir die Prozentzahlen besser zu merken, nennst du dies auch die 68-95-99,7 Regel.
Verteilungsfunktion Normalverteilung
Die Formel für die Verteilungsfunktion
ist dagegen etwas komplizierter. Eine Verteilungsfunktion beschreibt die eingeschlossene Fläche unter der Funktion. Hier berechnest du also die Fläche unter der Gaussverteilung. Dafür benötigst du ein Integral
, mit dem du die einzelnen Werte von – bis zum Wert t summierst.
bis zum Wert t summierst.
![Rendered by QuickLaTeX.com \[F(x) = \int_{-\infty}^{t} \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\cdot {(\frac{t-\mu}{\sigma}})^2} dt\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-04d7e280122d6a6b3cd287c8c3bce428_l3.png)
Übrigens: Wenn du den Teil 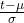 der Formel durch z substituierst, erhältst du die Verteilungsfunktion Φ der Standardnormalverteilung:
der Formel durch z substituierst, erhältst du die Verteilungsfunktion Φ der Standardnormalverteilung:
Substituiere
z = 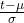
und du erhältst:
![Rendered by QuickLaTeX.com \[\phi (x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-\frac{1}{2} t^2} dt\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f9ca881827effa5054c22c36ae4dae82_l3.png)
Verteilungsfunktionen der Gaußschen Normalverteilung können grafisch so aussehen:
Aber keine Sorge! Solche Verteilungsfunktionen berechnest du nicht im Kopf. Du nutzt dafür sogenannte Verteilungstabellen. Mit ihnen kannst du das Ergebnis ganz einfach ablesen. Die Verteilungstabelle der Standardnormalverteilung findest weiter unten im Beitrag.
Annäherung an die Binomialverteilung
Du kannst dich mit der Gauss Normalverteilung der Binomialverteilung annähern. Diese Annäherung funktioniert vor allem mit einer großen Stichprobe, also einem großen n > 20.
Ist X∼B (n; p; k) mit
X = binomialverteilte Zufallsvariable
n = Anzahl der Ziehungen
p = Wahrscheinlichkeit eines Erfolgs
k = Anzahl der Erfolge
so gilt: P (X ≤ k) ≈ 
und P (l≤ X≤ k) ≈ 
Bei der Annäherung mit der Gaußschen Normalverteilung solltest du nun ein paar Dinge beachten:
- bei jeder Binomialverteilung ist der Erwartungswert μ= n ⋅p
- und die Standardabweichung σ = √σ² =

- nur bei großen Zahlen ist der Fehler durch die Annäherung klein
- Pass auf, wann du +0,5 und wann du -0,5 in die Formel einsetzt!
Normalverteilung Tabelle
Wenn die Rede von der Verteilungstabelle der Normalverteilung ist, ist im Normalfall die Tabelle der Standardnormalverteilung gemeint.
| z / Φ(z) | 0 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0 | 0,5 | 0,50399 | 0,50798 | 0,51197 | 0,51595 | 0,51994 | 0,52392 | 0,5279 | 0,53188 | 0,53586 |
| 0,1 | 0,53983 | 0,5438 | 0,54776 | 0,55172 | 0,55567 | 0,55962 | 0,56356 | 0,56749 | 0,57142 | 0,57535 |
| 0,2 | 0,57926 | 0,58317 | 0,58706 | 0,59095 | 0,59483 | 0,59871 | 0,60257 | 0,60642 | 06,1026 | 0,61409 |
| 0,3 | 0,61791 | 0,62172 | 0,62552 | 0,6293 | 0,63307 | 0,63683 | 0,64058 | 0,64431 | 0,64803 | 0,65173 |
| 0,4 | 0,65542 | 0,6591 | 0,66276 | 0,6664 | 0,67003 | 0,67364 | 0,67724 | 0,68082 | 0,68439 | 0,68793 |
| 0,5 | 0,69146 | 0,69497 | 0,69847 | 0,70194 | 0,7054 | 0,70884 | 0,71226 | 0,71566 | 0,71904 | 0,7224 |
| 0,6 | 0,72575 | 0,72907 | 0,73237 | 0,73565 | 0,73891 | 0,74215 | 0,74537 | 0,74857 | 0,75175 | 0,7549 |
| 0,7 | 0,75804 | 0,76115 | 0,76424 | 0,7673 | 0,77035 | 0,77337 | 0,77637 | 0,77935 | 0,7823 | 0,78524 |
| 0,8 | 0,78814 | 0,79103 | 0,79389 | 0,79673 | 0,79955 | 0,80234 | 0,80511 | 0,80785 | 0,81057 | 0,81327 |
| 0,9 | 0,81594 | 0,81859 | 0,82121 | 0,82381 | 0,82639 | 0,82894 | 0,83147 | 0,83398 | 0,83646 | 0,83891 |
| 1 | 0,84134 | 0,84375 | 0,84614 | 0,84849 | 0,85083 | 0,85314 | 0,85543 | 0,85769 | 0,85993 | 0,86214 |
| 1,1 | 0,86433 | 0,8665 | 0,86864 | 0,87076 | 0,87286 | 0,87493 | 0,87698 | 0,879 | 0,881 | 0,88298 |
| 1,2 | 0,88493 | 0,88686 | 0,88877 | 0,89065 | 0,89251 | 0,89435 | 0,89617 | 0,89796 | 0,89973 | 0,90147 |
| 1,3 | 0,9032 | 0,9049 | 0,90658 | 0,90824 | 0,90988 | 0,91149 | 0,91309 | 0,91466 | 0,91621 | 0,91774 |
| 1,4 | 0,91924 | 0,92073 | 0,9222 | 0,92364 | 0,92507 | 0,92647 | 0,92785 | 0,92922 | 0,93056 | 0,93189 |
| 1,5 | 0,93319 | 0,93448 | 0,93574 | 0,93699 | 0,93822 | 0,93943 | 0,94062 | 0,94179 | 0,94295 | 0,94408 |
| 1,6 | 0,9452 | 0,9463 | 0,94738 | 0,94845 | 0,9495 | 0,95053 | 0,95154 | 0,95254 | 0,95352 | 0,95449 |
| 1,7 | 0,95543 | 0,95637 | 0,95728 | 0,95818 | 0,95907 | 0,95994 | 0,9608 | 0,96164 | 0,96246 | 0,96327 |
| 1,8 | 0,96407 | 0,96485 | 0,96562 | 0,96638 | 0,96712 | 0,96784 | 0,96856 | 0,96926 | 0,96995 | 0,97062 |
| 1,9 | 0,97128 | 0,97193 | 0,97257 | 0,9732 | 0,97381 | 0,97441 | 0,975 | 0,97558 | 0,97615 | 0,9767 |
| 2 | 0,97725 | 0,97778 | 0,97831 | 0,97882 | 0,97932 | 0,97982 | 0,9803 | 0,98077 | 0,98124 | 0,98169 |
| 2,1 | 0,98214 | 0,98257 | 0,983 | 0,98341 | 0,98382 | 0,98422 | 0,98461 | 0,985 | 0,98537 | 0,98574 |
| 2,2 | 0,9861 | 0,98645 | 0,98679 | 0,98713 | 0,98745 | 0,98778 | 0,98809 | 0,9884 | 0,9887 | 0,98899 |
| 2,3 | 0,98928 | 0,98956 | 0,98983 | 0,9901 | 0,99036 | 0,99061 | 0,99086 | 0,99111 | 0,99134 | 0,99158 |
| 2,4 | 0,9918 | 0,99202 | 0,99224 | 0,99245 | 0,99266 | 0,99286 | 0,99305 | 0,99324 | 0,99343 | 0,99361 |
| 2,5 | 0,99379 | 0,99396 | 0,99413 | 0,9943 | 0,99446 | 0,99461 | 0,99477 | 0,99492 | 0,99506 | 0,9952 |
| 2,6 | 0,99534 | 0,99547 | 0,9956 | 0,99573 | 0,99585 | 0,99598 | 0,99609 | 0,99621 | 0,99632 | 0,99643 |
| 2,7 | 0,99653 | 0,99664 | 0,99674 | 0,99683 | 0,99693 | 0,99702 | 0,99711 | 0,9972 | 0,99728 | 0,99736 |
| 2,8 | 0,99744 | 0,99752 | 0,9976 | 0,99767 | 0,99774 | 0,99781 | 0,99788 | 0,99795 | 0,99801 | 0,99807 |
| 2,9 | 0,99813 | 0,99819 | 0,99825 | 0,99831 | 0,99836 | 0,99841 | 0,99846 | 0,99851 | 0,99856 | 0,99861 |
| 3 | 0,99865 | 0,99869 | 0,99874 | 0,99878 | 0,99882 | 0,99886 | 0,99889 | 0,99893 | 0,99896 | 0,999 |
| 3,1 | 0,99903 | 0,99906 | 0,9991 | 0,99913 | 0,99916 | 0,99918 | 0,99921 | 0,99924 | 0,99926 | 0,99929 |
| 3,2 | 0,99931 | 0,99934 | 0,99936 | 0,99938 | 0,9994 | 0,99942 | 0,99944 | 0,99946 | 0,99948 | 0,9995 |
| 3,3 | 0,99952 | 0,99953 | 0,99955 | 0,99957 | 0,99958 | 0,9996 | 0,99961 | 0,99962 | 0,99964 | 0,99965 |
| 3,4 | 0,99966 | 0,99968 | 0,99969 | 0,9997 | 0,99971 | 0,99972 | 0,99973 | 0,99974 | 0,99975 | 0,99976 |
| 3,5 | 0,99977 | 0,99978 | 0,99978 | 0,99979 | 0,9998 | 0,99981 | 0,99981 | 0,99982 | 0,99983 | 0,99983 |
| 3,6 | 0,99984 | 0,99985 | 0,99985 | 0,99986 | 0,99986 | 0,99987 | 0,99987 | 0,99988 | 0,99988 | 0,99989 |
| 3,7 | 0,99989 | 0,9999 | 0,9999 | 0,9999 | 0,99991 | 0,99991 | 0,99992 | 0,99992 | 0,99992 | 0,99992 |
| 3,8 | 0,99993 | 0,99993 | 0,99993 | 0,99994 | 0,99994 | 0,99994 | 0,99994 | 0,99995 | 0,99995 | 0,99995 |
| 3,9 | 0,99995 | 0,99995 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99997 | 0,99997 |
| 4 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99998 | 0,99998 | 0,99998 | 0,99998 |
Die Werte der ersten Zeile unter z und die Werte der ersten Spalte für  ergeben zusammen den gesuchten Wert. Um die Werte aus der Tabelle abzulesen, geht man folgendermaßen vor:
ergeben zusammen den gesuchten Wert. Um die Werte aus der Tabelle abzulesen, geht man folgendermaßen vor:
Das z steht dabei für den Wert bis zur ersten Nachkommastelle. Um den Wert auf die zweite Nachkommastelle genau zu bestimmen, addiert man den passenden Wert aus der ersten Zeile der Tabelle einfach hinzu. Anschließend kann man die gesuchte Verteilung an der Schnittstelle ablesen.
Der kleinste Wert der Tabelle der Gaußschen Normalverteilung ist 0. Da die Standardnormalverteilung symmetrisch ist, kann man aber auch die Wahrscheinlichkeit für negative Werte ablesen, indem man den positiven Wert von 1 subtrahiert.

Standardnormalverteilung berechnen
Du kannst jede beliebige Verteilung in die Standardnormalverteilung transformieren, indem du zuerst den Erwartungswert abziehst und anschließend durch die Standardabweichung teilst.

Es gilt also: 
Um Verwechslungen zu vermeiden, wird die standardisierte
Form der Verteilung mit  und nicht mit
und nicht mit  notiert.
notiert.
Standardnormalverteilung Tabelle
Nun benötigst du noch die oben abgebildete Verteilungstabelle der Standardnormalverteilung und kannst alle Wahrscheinlichkeiten ganz einfach ablesen. Da in der Tabelle nur positive Werte gelistet sind, musst du bei negativen Werten eine kurze Umrechnung durchführen. So berechnest du die Wahrscheinlichkeit, dass  :
:

Oder allgemein ausgedrückt:

Normalverteilung berechnen
Schau dir nun die Gaussverteilung an einem konkreten Beispiel an. Zur Berechnung mit der gaußschen Normalverteilung sind dir folgende Daten gegeben:
Die Brenndauer einer Kerze ist mit  und
und  normalverteilt.
normalverteilt.
N(40;7)
Normalverteilung Beispiel 1
Nun möchtest du die Wahrscheinlichkeit berechnen, dass die Kerze zwischen 33 und 47 Stunden brennt.

Als Erstes musst du deine Gaußsche Verteilung erstmal mit der eben erwähnten Formel standardisieren und vereinfachen:

Der Subtrahend hat einen negativen Wert. Um ihn in der Tabelle nachschlagen zu können, musst du ihn in einen positiven Wert umwandeln. Also:
![Rendered by QuickLaTeX.com \Phi\left(1\right)- [1-\Phi\left(1\right)]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-91ad13792ca220cf24b643f69d006f7d_l3.png)
Anschließend kannst du noch ausmultiplizieren:
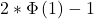
Um  herauszufinden, benötigst du nun die Tabelle der gaußschen Glockenkurve. Im Genaueren also die der Verteilungsfunktion der Standardnormalverteilung. Diese befindet sich wahrscheinlich hinten in deinem Skript oder in deiner Formelsammlung.
herauszufinden, benötigst du nun die Tabelle der gaußschen Glockenkurve. Im Genaueren also die der Verteilungsfunktion der Standardnormalverteilung. Diese befindet sich wahrscheinlich hinten in deinem Skript oder in deiner Formelsammlung.
Du suchst also in der Spalte z nach dem Wert 1 und kannst dann dein  ganz einfach ablesen. Es beträgt 0,8413.
ganz einfach ablesen. Es beträgt 0,8413.
Setzt du diesen Wert in deine Formel ein, kommst du auf ein Ergebnis von

Die Wahrscheinlichkeit, dass die Kerze zwischen 33 und 47 Stunden brennt, beträgt also 68,26%.
Normalverteilung Beispiel 2
Die Frage lässt sich natürlich auch anders herum stellen. Zum Beispiel: Wie lange brennt die Kerze mindestens mit einer Wahrscheinlichkeit von 70 Prozent?

Dazu bestimmst du das 70 %-Quantil und das geht so:
Zuerst schlägst du dein alpha-Quantil in der Verteilungstabelle nach. Achtung, hierfür gibt es nochmal eine neue Tabelle! Die Handhabung ist trotzdem die Gleiche wie eben.
Anschließend musst du dein neues  in das Quantil
in das Quantil  der tatsächlichen Gauß Verteilung transformieren. Dazu brauchst du folgende Formel:
der tatsächlichen Gauß Verteilung transformieren. Dazu brauchst du folgende Formel:

Also eigentlich berechnest du die umgekehrte Standardisierung. Die einzusetzenden Werte liest du wieder ganz einfach aus der Gaußschen Normalverteilung Tabelle ab.
Für dein Beispiel hieße das:

Deine Kerze brennt also mit einer Wahrscheinlichkeit von 70 % mindestens 43,5 Stunden.
Du siehst, so schwer ist die Gaußsche Normalverteilung gar nicht. Du musst nur den Umgang mit den Tabellen üben, damit du in der Klausur keine Zeit verlierst. Alles andere wird ein Kinderspiel.
Normalverteilung — häufigste Fragen
(ausklappen)
Normalverteilung — häufigste Fragen
(ausklappen)-
Was ist die Normalverteilung einfach erklärt?Die Normalverteilung ist eine glockenförmige Kurve, die zeigt, wie häufig bestimmte Werte vorkommen. In der Mitte liegt der Durchschnitt (Mittelwert), und je weiter man davon weggeht, desto seltener werden die Werte.
-
Wie erkennt man, ob eine Verteilung normal ist?Eine Verteilung ist normal, wenn sie symmetrisch um den Mittelwert liegt und die meisten Werte nahe an diesem Durchschnitt auftreten. Typisch ist eine glockenförmige Kurve, bei der Ausreißer nach links und rechts seltener werden.
-
Wie berechnet man die Normalverteilung?Um die Normalverteilung zu berechnen, rechnet man zuerst den sogenannten z-Wert aus: z = (x – µ) / σ. Er zeigt, wie viele Standardabweichungen ein Wert vom Mittelwert entfernt ist. Danach kann man in der z-Tabelle ablesen, wie wahrscheinlich es ist, dass ein Wert kleiner oder gleich x ist.
-
Was ist der Unterschied zwischen Standardnormalverteilung und Normalverteilung?Die Standardnormalverteilung ist eine spezielle Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1. Die Normalverteilung kann beliebige Werte für Mittelwert und Streuung haben.
-
Was zeigt der Erwartungswert bei einer Normalverteilung?Der Erwartungswert ist der Mittelwert der Verteilung. Er liegt genau in der Mitte der Glockenkurve — dort, wo die Wahrscheinlichkeit am höchsten ist.
Standardnormalverteilung
Super! Jetzt kennst du die Definition und die Formel einer Gaußschen Normalverteilung. Außerdem kennst du nun den Begriff Gaußsche Glockenkurve für die Normalverteilung. Wenn du dir die Besonderheiten der Standardnormalverteilung noch genauer anschauen willst, ist dieses Video genau das richtige für dich! Viel Spaß!










