Pumping Lemma

Pumping Lemma Definition

Das Pumping Lemma, auch Schleifensatz genannt, stellt in der theoretischen Informatik eine Bedingung für die Eigenschaft einer formalen Sprache dar. Mit ihm kann gezeigt werden, ob es sich bei einem Ausdruck um eine reguläre oder kontextfreie Sprache handelt.

direkt ins Video springen

Pumping Lemma einfach erklärt!

Das Prinzip des Pumping Lemma einfach erklärt:

„Beweis durch Widerspruch“

Das bedeutet nichts anderes, als zu zeigen, dass Sprachen, die nicht regulär oder nicht kontextfrei sind, das Pumping Lemma verletzen. Dabei muss aber beachtet werden, dass das nicht automatisch heißt, dass sobald ein Pumping Lemma erfüllt wird, es sich auch wirklich um eine reguläre oder kontextfreie Sprache handelt. In unseren Videos zu reguläre Sprachen  oder kontextfreien Sprachen erfährst du, wie man Regularität nachweist.

Für den Widerspruchsnachweis muss aber zwischen dem Pumping Lemma für reguläre Sprachen und kontextfreie Sprachen unterschieden werden. Im Allgemeinen können  aber durch das Lemma Wörter beliebig vergrößert oder verkleinert, oder in anderen Worten auch auf- bzw. abgepumpt werden. Ist dies nicht möglich, gilt die Bedingung als verletzt.

Pumping Lemma Reguläre Sprachen

Reguläre Sprachen lassen sich durch endliche Automaten erzeugen. Beispielsweise der folgende Automat:

direkt ins Video springen

Der Automat beschreibt eine Sprache, die aus den Wörtern 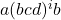besteht. Im hinteren Teil des Automaten ist also direkt eine Schleife zu erkennen, besteht aus b, c und d. Mit dem Pumping Lemma für reguläre Sprachen lässt sich die Schleife also beliebig oft durchlaufen.

Formale Definition

Formal lässt sich das Lemma wie folgt definieren:

Gegeben ist dabei die Sprache . Wörter der Sprache, die mindesten eine Länge n aufweisen, lassen sich so in die Teile und zerlegen, wodurch drei Eigenschaften gelten:

• Die beiden Teilwörter und haben zusammen höchstens die Länge
• Das Wort ist nicht leer
• Für jede Zahl ist das Wort in der Sprache.

N wird auch Pumping-Zahl genannt. Sie muss mindestens so lang sein, dass das Wort den Anfangsteil , den Endteil und den Schleifenteil des Automaten umfasst.

Das Schleifenteil pumpt das Wort auf oder ab. Entsprechend darf der Schleifenteil des Wortes natürlich nicht die leere Menge sein, ansonsten würde die Möglichkeit bestehen, dass jedes beliebige Wort aufgepumpt werden könnte. Die dritte Bedingung sagt nun, dass man ein Wort aus L mit dem Schleifenteil beliebig groß aufpumpen können muss.

Innerhalb des oben genannten Automaten wäre:

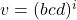
Dadurch können nun alle Wörter der Sprache erzeugt werden, z.B.:

• ist
• ist

Pumping Lemma Beispiel

Für unser Pumping Lemma Beispiel ist die folgende Sprache gegeben:

Die Wörter der Sprache L bestehen aus einer beliebigen, positiven Anzahl a’s gefolgt von noch mehr b’s. Formal geht man zunächst davon aus, dass es sich hierbei um eine reguläre Sprache handelt. Im nächsten Schritt soll dann ein Wort x aus der Sprache ausgewählt werden. In diesem Fall kann das beispielsweise sein.

Das Wort entspricht der Sprache, da mehr b’s als a’s enthalten sind. Die Wortlänge beträgt dabei {2n + 1} und ist damit länger als die Pumping Zahl.

Pumping Lemma Beweis

Laut Lemma ist es nun möglich, das Wort beliebig auf- oder abzupumpen. Die neu erzeugten Wörter müssen dabei immer in der Sprache liegen. Der Pump-Faktor wird dabei mit bezeichnet.

Mit dem -Teil können beliebig viele a’serzeugt werden, da das Ganze unabhängig von verläuft. Dadurch können immer mehr a’s als b’s erzeugt werden, wodurch letztendlich das Lemma widerlegt wird.

Für den Pumping Lemma Beweis werden nun die Exponenten zusammengefasst:

Im nächsten Schritt wird nun ein gewählt, mit dem die Bedingung des Lemma verletzt wird, bspw. :

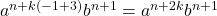
Vergleiche Exponenten: :

Da größer als Null sein muss, erhält man für mehr a’s im Wort als b’s. Das Pumping Lemma ist verletzt und die Sprache gilt nun offiziell als nicht regulär.

Allgemein gilt: Alle Sprachen, die in irgendeiner Weise ein Mitzählen von Bestandteilen eines Wortes erfordern, gelten als nicht regulär!

Pumping Lemma Kontextfreie Sprache

Durch das Pumping Lemma für kontextfreie Sprache, kann nur gezeigt werden, dass eine Sprache nicht kontextfrei ist. Um zu zeigen, dass es sich um eine kontextfreie Sprache handelt, muss eine kontextfreie Grammatik angegeben werden, die diese erzeugt.

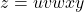Gegeben sei dabei wieder eine Sprache , die eine natürlichen Zahl besitzt. Dabei lassen sich alle Wörter in , die mindestens eine Länge von aufweisen mit darstellen. Dabei gelten die folgenden drei Bedingungen:

• Die drei Teilwörter , und haben zusammen höchstens die Länge
• Das Wort oder ist nicht leer
• Für jede Zahl ist das Wort in der Sprache.

Pumping Lemma Aufgabe

Als weiteres Beispiel, folgt nun eine Aufgabe, in der nachgewiesen werden soll, dass es sich bei der Sprache nicht um eine kontextfreie Sprache handelt. Gegeben sei dafür:

Zu beginn wird angenommen, dass die Sprache kontextfrei ist. Das Wort ist dabei mindestens so groß wie die Pumping-Länge , weshalb gilt:

Im nächsten Schritt wird versucht die Wortteile und -mal zu wiederholen.

Ergibt sich hierbei ein Wort, das nicht in der Sprache liegt, gilt die Sprache als nicht kontextfrei.

Pumping Lemma Beweis

Für den Beweis bildet man ein Wort   mit der Pumping-Zahl , bspw.:

, und dürfen höchstens -Zeichen lang sein. Für ergibt sich das Wort

Versucht man dann das Wort so zu zerteilen, dass im Teilwort 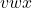alle drei Zeichen auftreten, überschreitet man das von 2. Daraus folgt, dass in 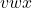nur maximal zwei verschiedene Buchstaben vorkommen können.

Innerhalb von  lassen sich nie alle drei Buchstaben vervielfachen, da im Teilwort 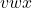nie alle drei Buchstaben enthalten sein können. Dadurch wird im Wort beispielsweise nur die Buchstaben und vervielfacht, aber das nicht. Dadurch befindet sich das Wort nicht mehr in der Sprache und ist somit nicht kontextfrei.