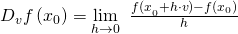Richtungsableitung
Die Richtungsableitung gibt die lokale Änderungsrate des Funktionswertes einer reellwertigen Funktion bei einer Änderung der Funktionsvariablen in eine vorgegebene Richtung an. Entspricht diese Richtung derjenigen, des 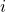 -ten Basisvektors, so ist die Richtungsableitung gleich der
-ten Basisvektors, so ist die Richtungsableitung gleich der 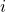 -ten partiellen Ableitung. Im Falle der totalen Differenzierbarkeit
lässt sich auch mithilfe des Gradienten
die Richtungsableitung berechnen.
-ten partiellen Ableitung. Im Falle der totalen Differenzierbarkeit
lässt sich auch mithilfe des Gradienten
die Richtungsableitung berechnen.
Das Wichtigste rund um dieses Thema haben wir für Dich in unserem Video zusammengefasst!
Inhaltsübersicht
Schreibweisen
Gelegentlich werden statt 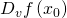 auch folgende Schreibweisen verwendet:
auch folgende Schreibweisen verwendet:
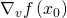
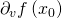
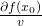
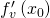
Richtungsableitung Beispiel
Zur Verdeutlichung soll in einem Beispiel konkret gezeigt werden, wie die Richtungsableitung einer Funktion anhand der Definition berechnet werden kann. Hierzu soll die Ableitung für die Funktion 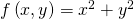 an der allgemeinen Stelle
an der allgemeinen Stelle 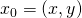 in Richtung
in Richtung 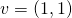 bestimmt werden.
bestimmt werden.
Einsetzen in die Definition liefert:
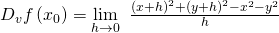
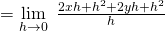
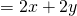
Einseitige Richtungsableitung
Analog zur einseitigen Ableitung reellwertiger Funktionen einer Variablen lassen sich auch einseitige Richtungsableitungen definieren:
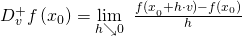
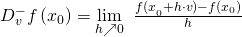
Bedeutung der Richtungsableitung
Aus der Definition der Richtungsableitung lassen sich gewisse Ähnlichkeiten zum Differentialquotienten und zur Definition der partiellen Ableitung einer Funktion ablesen. Diese spiegeln sich auch in der Bedeutung der Richtungsableitung wieder.
Für Funktionen einer Variablen gibt der Differentialquotient bekannterweise die lokale Änderungsrate des Funktionswertes an der untersuchten Stelle an. Werden reellwertige Funktionen mehrerer Variablen untersucht, so geben die partiellen Ableitungen die lokale Änderungsrate bei einer Bewegung in eine der Koordinatenrichtungen an. Sie sind somit ein Spezialfall der Richtungsableitungen. Diese geben nämlich die lokale bzw. momentane Änderungsrate in eine durch den Vektor  vorgegebene Richtung an.
vorgegebene Richtung an.
Richtungsableitung und partielle Ableitungen
Ist dieser vorgegebene Richtungsvektor  beispielsweise der
beispielsweise der 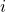 -te Basisvektor
-te Basisvektor 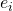 , so gilt für die Ableitung in diese Richtung an der Stelle
, so gilt für die Ableitung in diese Richtung an der Stelle 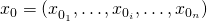 :
:
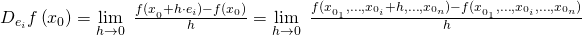
Dies entspricht gerade der 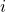 -ten partiellen Ableitung
von
-ten partiellen Ableitung
von 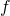 in
in 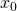 :
:
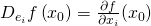
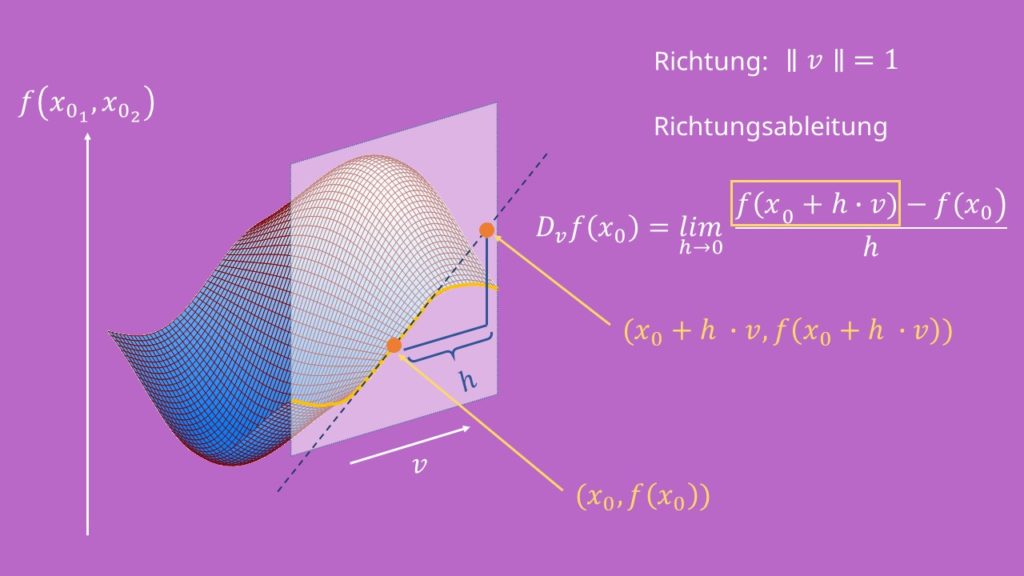
Wird eine reellwertige Funktion betrachtet, die von zwei Variablen abhängt, so kann deren Graph als dreidimensionale Hügellandschaft angesehen werden und die Bedeutung der Richtungsableitung lässt sich in diesem Fall gut veranschaulichen. Die 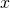 – und
– und 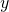 -Komponente des Graphen sind die beiden Variablen der Funktion und die
-Komponente des Graphen sind die beiden Variablen der Funktion und die  -Komponente ist der Funktionswert an dieser Stelle. Die Richtungsableitung in Richtung
-Komponente ist der Funktionswert an dieser Stelle. Die Richtungsableitung in Richtung  gibt dann die Steigung der Hügellandschaft an, wenn man sich von der Stelle
gibt dann die Steigung der Hügellandschaft an, wenn man sich von der Stelle 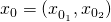 aus in die Richtung des Vektors
aus in die Richtung des Vektors  bewegen würde. Wird der Funktionsgraph mit einer Ebene geschnitten, die den Punkt
bewegen würde. Wird der Funktionsgraph mit einer Ebene geschnitten, die den Punkt 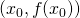 enthält, senkrecht auf der
enthält, senkrecht auf der 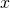 –
–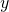 -Ebene steht und in Richtung des Vektors
-Ebene steht und in Richtung des Vektors  verläuft, so ergibt sich eine Schnittkurve, deren Tangentensteigung an der Stelle
verläuft, so ergibt sich eine Schnittkurve, deren Tangentensteigung an der Stelle 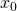 gerade die gesuchte Richtungsableitung ist.
gerade die gesuchte Richtungsableitung ist.
Richtungsableitung berechnen
In einem Beispiel wurde bereits gezeigt wie mittels der Definition die Richtungsableitung einer Funktion berechnet werden kann. Allerdings muss hierzu ein Grenzwert berechnet werden, was nicht immer so einfach gelingt, wie in dem gezeigten Beispiel. Daher wird die Richtungsableitung meist mithilfe des Gradienten der Funktion bestimmt. Es gilt nämlich ein sehr nützlicher Zusammenhang zwischen dem Gradienten der Funktion und den Richtungsableitungen.
Richtungsableitung und Gradient
Sei 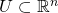 eine offene Menge und
eine offene Menge und 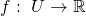 eine stetig total differenzierbare Funktion. Sei außerdem
eine stetig total differenzierbare Funktion. Sei außerdem 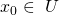 ein Punkt aus
ein Punkt aus 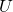 und
und 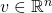 ein Vektor mit
ein Vektor mit 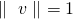 . Dann gilt:
. Dann gilt:
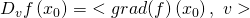
Dabei bezeichnet 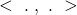 das gewöhnliche Skalarprodukt. Da der Gradient gerade die Transponierte der totalen Ableitung bzw. der Jacobi-Matrix
das gewöhnliche Skalarprodukt. Da der Gradient gerade die Transponierte der totalen Ableitung bzw. der Jacobi-Matrix 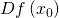 von
von 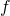 darstellt, kann diese Gleichung auch folgendermaßen geschrieben werden:
darstellt, kann diese Gleichung auch folgendermaßen geschrieben werden:
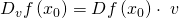
Mit diesem Wissen lässt sich immer auf dieselbe Art und Weise vorgehen, um die Ableitung einer Funktion 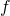 an der Stelle
an der Stelle 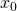 in Richtung
in Richtung  zu berechnen. Dabei könnte es der Fall sein, dass der vorgegebene Richtungsvektor
zu berechnen. Dabei könnte es der Fall sein, dass der vorgegebene Richtungsvektor  noch nicht normiert ist, also noch nicht die Länge 1 besitzt. Um den richtigen Wert für die Ableitung zu erhalten, muss man diesen dann gegebenenfalls noch normieren. Die einzelnen Schritte zur Berechnung der Richtungsableitung sehen dann wie folgt aus:
noch nicht normiert ist, also noch nicht die Länge 1 besitzt. Um den richtigen Wert für die Ableitung zu erhalten, muss man diesen dann gegebenenfalls noch normieren. Die einzelnen Schritte zur Berechnung der Richtungsableitung sehen dann wie folgt aus:
I. Den Gradienten von 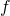 an der Stelle
an der Stelle 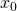 bestimmen:
bestimmen:
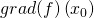
II. Den gegebenen Richtungsvektor  normieren:
normieren:
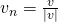
III. Das Skalarprodukt des Gradienten und des normierten Vektors berechnen:
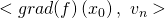
Die Berechnung der Richtungsableitung soll anhand eines Beispiels im Folgenden einmal dargelegt werden.
Beispiel: Richtungsableitung berechnen
Es soll die Ableitung der Funktion 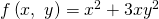 an der Stelle
an der Stelle 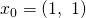 in Richtung des Vektors
in Richtung des Vektors 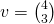 berechnet werden. Dazu werden die oben beschriebenen Schritte abgearbeitet:
berechnet werden. Dazu werden die oben beschriebenen Schritte abgearbeitet:
I. Dem Gradienten von 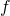 an der Stelle
an der Stelle 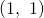 bestimmen:
bestimmen:
Der Gradient der Funktion 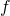 an der allgemeinen Stelle
an der allgemeinen Stelle 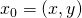 lautet:
lautet:
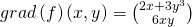
Durch einsetzen der Stelle 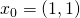 ergibt sich der gesuchte Gradient:
ergibt sich der gesuchte Gradient:
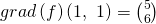
II. Den gegebenen Richtungsvektor  normieren:
normieren:
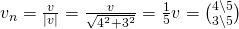
III. Das Skalarprodukt des Gradienten und des normierten Vektors berechnen:
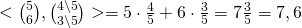
Die gesuchte Richtungsableitung der Funktion besitzt also den Wert 7,6.
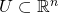 offen und
offen und 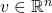 ein Vektor mit
ein Vektor mit