Kugelkoordinaten
In diesem Artikel betrachten wir die Kugelkoordinaten und deren Transformation mit kartesischen Koordinaten genauer. Dazu zählen auch die Transformationen der Differentiale, des Flächen-, Volumen– und Linienelements sowie die Transformation der Basisvektoren, des Nabla– und des Laplaceoperators.
Das Wichtigste zum Thema Kugelkoordinaten haben wir außerdem in einem kurzen Video für dich aufbereitet. Das fördert die Vorstellung und kann dir das Thema einfacher näher bringen.
Inhaltsübersicht
Kugelkoordinaten Definition
Wird der Abstand vom Ursprung konstant gehalten, so spricht man von sphärischen Koordinaten. Die betrachteten Punkte liegen dann auf einer Kugeloberfläche.
Kugelkoordinatensystem
Um einen Punkt im Raum beschreiben zu können, ist ein Koordinatensystem von Nöten. In Kugelkoordinaten ist das Koordinatensystem durch folgende Punkte festgelegt:
- das Zentrum
 bzw. der Ursprung des Koordinatensystems.
bzw. der Ursprung des Koordinatensystems. - eine gerichtete Gerade durch den Ursprung. Diese nennt man Polachse und ihre Richtung wird als Polrichtung bezeichnet. Die Polachse gibt zudem die sogenannte Äquatorebene vor. Diese Ebene liegt orthogonal zur Polrichtung und verläuft durch den Ursprung.
- eine Bezugsrichtung, d.h. eine Halbgerade in der Äquatorebene.
Um Umrechnungen mit den kartesischen Koordinaten zu vereinfachen, lassen sich die genannten Punkte so festlegen, dass der Ursprung des Kugelkoordinatensystems dem des kartesischen Systems entspricht. Des weiteren kann die  -Achse als Polachse verwendet werden, sodass die
-Achse als Polachse verwendet werden, sodass die  –
– -Ebene der Äquatorebene entspricht. Die positive
-Ebene der Äquatorebene entspricht. Die positive  -Achse kann zudem als Bezugsrichtung gewählt werden.
-Achse kann zudem als Bezugsrichtung gewählt werden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Kugelkoordinatendarstellung
Wie bereits erwähnt, wird ein Punkt in Kugelkoordinaten unter anderem durch zwei Winkel angegeben. Wie diese gewählt werden unterscheidet sich allerdings je nach Konvention. Im Folgenden soll derjenigen Konvention gefolgt werden, welche in der Mathematik und der Physik üblich ist. Ein Punkt  im Raum ist dann durch folgende drei Koordinaten gegeben:
im Raum ist dann durch folgende drei Koordinaten gegeben:
- den Abstand
 des Punktes
des Punktes  vom gewählten Koordinatenursprung
vom gewählten Koordinatenursprung  . Dieser wird auch als Radius bezeichnet und definiert eine Kugeloberfläche, auf der sich der Punkt befindet. Er entspricht der Länge der Strecke
. Dieser wird auch als Radius bezeichnet und definiert eine Kugeloberfläche, auf der sich der Punkt befindet. Er entspricht der Länge der Strecke  .
. - den Winkel
 zwischen der Strecke
zwischen der Strecke  und der oberen Halbgerade der Polachse. Der Winkel wird nur von
und der oberen Halbgerade der Polachse. Der Winkel wird nur von  bis
bis  (
( bis
bis  ) gezählt und er legt eine Kreislinie auf der Kugeloberfläche fest, auf der sich der Punkt
) gezählt und er legt eine Kreislinie auf der Kugeloberfläche fest, auf der sich der Punkt  befindet. Man nennt ihn Polarwinkel oder Poldistanzwinkel.
befindet. Man nennt ihn Polarwinkel oder Poldistanzwinkel. - den Winkel
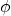 zwischen der Bezugsrichtung und der Projektion der Strecke
zwischen der Bezugsrichtung und der Projektion der Strecke  auf die Äquatorebene. Man misst den Winkel gegen den Uhrzeigersinn zwischen
auf die Äquatorebene. Man misst den Winkel gegen den Uhrzeigersinn zwischen  und
und  (
( und
und  ) oder
) oder  und
und  (
( und
und  ) und nennt ihn auch Azimutwinkel. Er definiert nun den Ort des Punktes
) und nennt ihn auch Azimutwinkel. Er definiert nun den Ort des Punktes  auf der Kreislinie.
auf der Kreislinie.
Ein Punkt im Raum wird also durch die Angabe dieser drei Koordinaten  in Kugelkoordinaten beschrieben.
in Kugelkoordinaten beschrieben.
Kugelkoordinaten umrechnen
Zur Vereinfachung von Rechnungen sind häufig Umrechnungen zwischen dem kartesischen und dem Kugelkoordinatensystem erforderlich. Diese sollen im Folgenden in beide Richtungen aufgezeigt werden.
Kartesische Koordinaten in Kugelkoordinaten umrechnen
Wird der Azimutwinkel 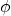 zwischen
zwischen  und
und  (
( und
und  ) angegeben, so können die Kugelkoordinaten wie folgt berechnet werden:
) angegeben, so können die Kugelkoordinaten wie folgt berechnet werden:


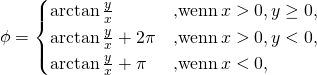
Andere Konventionen
In der beschriebenen Konvention entspricht der Polarwinkel  nicht der geographischen Breite, welche nämlich den Winkel zwischen dem Ortsvektor und der Äquatorebene beschreibt. Sie nimmt also im Gegensatz zum Polarwinkel nach obiger Konvention Werte zwischen
nicht der geographischen Breite, welche nämlich den Winkel zwischen dem Ortsvektor und der Äquatorebene beschreibt. Sie nimmt also im Gegensatz zum Polarwinkel nach obiger Konvention Werte zwischen  und
und  an. Man kann allerdings mit
an. Man kann allerdings mit 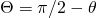 auch die folgende Darstellung der Kugelkoordinaten verwenden:
auch die folgende Darstellung der Kugelkoordinaten verwenden:



Dann entspricht der Winkel  der geographischen Breite. In beiden Konventionen kann der Winkel
der geographischen Breite. In beiden Konventionen kann der Winkel 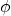 als geographische Länge identifiziert werden.
als geographische Länge identifiziert werden.
Transformation von Differentialen
Im Folgenden sollen die wichtigsten Differentiale mithilfe der Jacobi-Matrix und der Funktionaldeterminante transformiert werden.
Jacobi-Matrix und Funktionaldeterminante
Die Jacobi-Matrix der Transformation von Kugelkoordinaten in kartesische Koordinaten lautet folgendermaßen:

Dementsprechend lautet die Funktionaldeterminante folgendermaßen:
det
Differentiale (Volumenelement, Flächenelement, Linienelement)
Mithilfe der Jacobi-Matrix lassen sich die Differentiale durch folgende Lineare Abbildung bestimmten:

So können nun auch das Volumen-, Flächen– und Linienelement bestimmt werden.
Diese lassen sich auch auf anderem Wege ermitteln. Das Volumenelement  kann nämlich ganz einfach mithilfe der Funktionaldeterminante bestimmt werden:
kann nämlich ganz einfach mithilfe der Funktionaldeterminante bestimmt werden:

Das Flächenelement  ergibt sich dann durch Differentiation:
ergibt sich dann durch Differentiation:

Für das Linienelement  gilt:
gilt:

Transformation von Basisvektoren und Vektoroperatoren
Neben den Einheitsvektoren sollen im Folgenden auch der Nabla– und der Laplaceoperator in Kugelkoordinaten bestimmt werden.
Einheitsbasisvektoren
Mit dem Richtungsvektor

gilt für die Einheitsvektoren:



Partielle Ableitungen (Nabla- und Laplaceoperator)
Die partiellen Ableitungen können mithilfe der Jacobi-Matrix der Transformation und ihrer Inversen auf folgende Art berechnet werden:


Durch entsprechende Transformation der partiellen Ableitungen und der Einheitsvektoren ergibt sich der Nablaoperator in Kugelkoordinaten:

Mithilfe dieses Nablaoperators kann dann für ein Skalarfeld der Gradient in Kugelkoordinaten bestimmt werden. Ist ein Vektorfeld  gegeben, so lautet die Divergenz in Kugelkoordinaten für dieses Feld folgendermaßen:
gegeben, so lautet die Divergenz in Kugelkoordinaten für dieses Feld folgendermaßen:

Für die Rotation in Kugelkoordinaten gilt:

Der Laplaceoperator lässt sich nun ganz einfach bestimmen, indem man in der Formel für die Divergenz als Vektorfeld den Nablaoperator einsetzt:

Sphärische Koordinaten
Hält man in Kugelkoordinaten den Radius  konstant und lässt nur für die beiden Winkel
konstant und lässt nur für die beiden Winkel  und
und 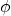 verschiedene Werte zu, so befinden sich alle möglichen Punkte auf der Oberfläche einer Kugel mit dem Radius
verschiedene Werte zu, so befinden sich alle möglichen Punkte auf der Oberfläche einer Kugel mit dem Radius  und dem Mittelpunkt im Koordinatenursprung. Man spricht dann von sphärischen Koordinaten.
und dem Mittelpunkt im Koordinatenursprung. Man spricht dann von sphärischen Koordinaten.


 umrechnen, so gelangt man durch geometrische Überlegungen zu folgenden Formeln:
umrechnen, so gelangt man durch geometrische Überlegungen zu folgenden Formeln:

