Monoton steigend und fallend
Du fragst dich, was Monotonie ist und wie du sie erkennen kannst? In diesem Beitrag und im Video zeigen wir dir, wie Monotonie Funktionen beschreibt und was streng monoton steigend und fallend überhaupt bedeutet.
Inhaltsübersicht
Monotonie einer Funktion einfach erklärt
Die Monotonie beschreibt den Verlauf einer Funktion. Das Monotonieverhalten sagt dabei aus, ob der Graph der Funktion in einem Intervall steigt, fällt oder konstant bleibt. Du unterscheidest dabei zwischen vier verschiedenen Fällen.
Graph verläuft nach oben:
- streng monoton steigend (I) oder
- monoton steigend (II).
Graph verläuft nach unten:
Wie du die einzelnen Fälle voneinander unterscheiden kannst, sehen wir uns jetzt an.
Streng monoton steigend
Wenn eine Funktion in einem betrachteten Intervall durchgehend nach oben geht, bezeichnest du sie als streng monoton steigend. Die Steigung einer streng monotonen Funktion muss also immer größer als 0 sein.
Eine Funktion f ist also streng monoton steigend, wenn bei einer Erhöhung des x-Wertes auch der Funktionswert f(x) größer wird.
Es gilt: 
Die erste Ableitung
 ist im Fall einer streng monotonen Steigung immer positiv, egal welchen Punkt du im Intervall untersuchst. Es gilt für alle
ist im Fall einer streng monotonen Steigung immer positiv, egal welchen Punkt du im Intervall untersuchst. Es gilt für alle  :
: 
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Monoton steigend
Es ist jedoch nicht jede Funktion mit steigendem Graphen auch streng monoton steigend. Eine Funktion ist in einem Intervall nur monoton steigend, wenn sie grundsätzlich steigt, aber an manchen Stellen konstant bleibt. Jeder Punkt der Funktion muss also eine Steigung von 0 oder größer haben.
Eine Funktion f ist also monoton steigend, wenn bei einer Erhöhung des x-Wertes auch der Funktionswert f(x) größer wird oder gleich bleibt.
Es gilt: 
Die erste Ableitung  ist in diesem Fall immer mindestens 0. Steigt der Graph an, ist die Ableitung positiv. Ist er konstant, ist die Ableitung an diesem Punkt gleich 0. Es gilt für alle
ist in diesem Fall immer mindestens 0. Steigt der Graph an, ist die Ableitung positiv. Ist er konstant, ist die Ableitung an diesem Punkt gleich 0. Es gilt für alle  :
: 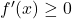
Streng monoton fallend
Eine Funktion gilt in einem Intervall als streng monoton fallend, wenn sie in diesem Abschnitt durchgehend fällt. Das bedeutet, dass der Graph der Funktion an jedem Punkt eine Steigung unter 0 hat.
Eine Funktion f ist also streng monoton fallend, wenn bei einer Erhöhung des x-Wertes der Funktionswert f(x) kleiner wird.
Es gilt: 
Da hier auch eine strenge Monotonie vorliegt, darf die erste Ableitung  an keinem Punkt 0 sein. Stattdessen ist sie immer negativ. Es gilt für alle
an keinem Punkt 0 sein. Stattdessen ist sie immer negativ. Es gilt für alle  :
: 
Monoton fallend
Es gibt aber auch Funktionen, die in einem Intervall sowohl fallen als auch konstant bleiben und daher als monoton fallend bezeichnet werden. Der Graph hat im ausgewählten Intervall also eine Steigung von 0 oder weniger.
Eine Funktion f ist also monoton fallend, wenn bei einer Erhöhung des x-Wertes der Funktionswert f(x) kleiner wird oder gleich bleibt.
Es gilt: 
Wenn eine Funktion monoton fallend verläuft, ist die erste Ableitung  an konstanten Punkten 0 und sonst immer negativ. Es gilt für alle
an konstanten Punkten 0 und sonst immer negativ. Es gilt für alle  :
: 
Wenn eine Funktion in einem Intervall weder steigt noch fällt, wird sie auch konstante Funktion genannt. Da jeder x-Wert denselben Funktionswert f(x) annimmt, ist die erste Ableitung und damit auch die Steigung immer 0. Das ist zum Beispiel bei der Funktion f(x) = 4 der Fall.
Monotonieverhalten bestimmen
Sehr gut! Jetzt weißt du über Monotonie und die unterschiedlichen Monotoniearten Bescheid. Wie du das Monotonieverhalten rechnerisch bestimmen kannst, zeigen wir dir hier.





