Video

Quiz

Hier geht's zum Video „Differentialquotient“

Hier geht's zum Video „Produktregel“

h Methode

Wichtige Inhalte in diesem Video

H-Methode einfach erklärt

Differentialquotient h Methode

H Methode Aufgaben

In diesem Artikel erklären wir dir die h Methode, eine Methode aus dem Bereich der Differentialrechung, und zeigen dir Beispiele dazu.

Anschaulich und leicht verständlich findest du alles Wichtige zur h Methode in unserem Video . Schau es dir unbedingt an!

Inhaltsübersicht

H-Methode einfach erklärt

im Videozur Stelle im Video springen

Angenommen du hast eine Funktion f(x) gegeben. Dann kannst du dir mit der h-Methode ihre Ableitungsfunktion f'(x) herleiten.

Merke

Die h Methode lautet:

$f'(x)=\lim \limits_{h\to 0} \frac{f(x+h)-f(x)}{h}.$

Sie ist eine andere Interpretation des Differentialquotienten und berechnet daher die Steigung der Tangente am Punkt

Differentialquotient h Methode

im Videozur Stelle im Video springen

Der Differentialquotient

$\lim \limits_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}$

berechnet die Steigung der Funktion am Punkt x_0. Er stellt den Grenzwert des Differenzenquotienten dar. Graphisch gesehen bestimmst du über den Differentialquotient die Steigung der Tangente des Graphen am Punkt x_0, indem du immer mehr an x_0 annäherst.

h Methode Tangente Sekante Ableitung — h Methode

Das bedeutet, du reduzierst den Abstand zwischen und x_0 . Genau diese Sichtweise machst du dir bei der h-Methode zunutze und bezeichnest deshalb den Abstand als

h=x-x_0.

Diese Gleichung löst du nach x=x_0+h auf und setzt h und x in den Differentialquotienten ein. Da du nun den Abstand gegen Null laufen lässt, schreibst du im Grenzwert $h\to 0.$ Das Ergebnis ist die H Formel für den Punkt x_0:

$f'(x_0)=\lim \limits_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}=\lim \limits_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}.$

H Methode Aufgaben

im Videozur Stelle im Video springen

Schauen wir uns nun ein Beispiel an und zwar die Funktion

f(x)= x^2.

Du kannst nun die Ableitung der Funktion mithilfe der h-Methode herleiten. Dafür setzt du einfach die Funktion in die obere Formel ein:

$f'(x)=\lim \limits_{h\to 0} \frac{f(x+h)-f(x)}{h}$

$=\lim \limits_{h\to 0} \frac{(x+h)^2-x^2}{h}.$

Als nächstes löst du die quadratische Klammer im Zähler mit der Binomischen Formel auf und fasst den Term zusammen:

$f'(x)= \lim \limits_{h\to 0} \frac{x^2 +2xh + h^2 - x^2}{h}$

$=\lim \limits_{h\to 0} \frac{2xh + h^2}{h}.$

Nun kannst du im Zähler ein ausklammern und im Anschluss mit dem im Nenner kürzen:

$f'(x)=\lim \limits_{h\to 0} \frac{h\cdot (2x + h)}{h}$

$= \lim \limits_{h\to 0} 2x + h.$

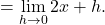
Schließlich bestimmst du den Grenzwert, indem du für Null einsetzt. Damit ergibt sich die Ableitung

f'(x)=2x.

Falls du noch mehr Beispiele zur Ableitung h Methode sehen möchtest, findest du sie in den Artikeln:

Funktionen und ihre Ableitungen

Wie du siehst kannst du mit der beschriebenen Methode die Ableitung von bestimmten Funktionen herleiten, wie auch die der folgenden:

	Funktion	Ableitung
e Funktion ableiten
ln ableiten	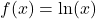$f(x)=\ln(x)$	$f'(x)=\frac{1}{x}$
Wurzel ableiten	$f(x)=\sqrt{x}$	$f'(x)=\frac{1}{2\sqrt{x}}$
Ableitung Cosinus	$f(x)=\cos(x)$	$f'(x)=-\sin(x)$
Ableitung Sinus	$f(x)=\sin(x)$	$f'(x)=\cos(x)$
Ableitung Tangens	$f(x)=\tan(x)$	$f'(x)=\frac{1}{\cos^2(x)}$

Ableitungsregeln

Tatsächlich ist es möglich mit dieser Methode, nicht nur explizite Ableitungen, sondern auch die nachstehenden Ableitungsregeln herzuleiten:

Ableitungsregel	Funktion	Ableitung
Summenregel
Differenzregel
Potenzregel		$f'(x)=n\cdot x^{n-1}$
Faktorregel	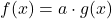$f(x)=a\cdot g(x)$	$f'(x)=a \cdot g'(x)$
Produktregel	$f(x)=g(x)\cdot h(x)$	$f'(x)=g'(x)\cdot h(x)+g(x)\cdot h'(x)$
Quotientenregel	$f(x)=\frac{g(x)}{h(x)}$	$f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}$
Kettenregel		$f'(x)=g'(h(x))\cdot h'(x)$

zur Videoseite: h Methode

Beliebte Inhalte aus dem Bereich Analysis

Mittlere Änderungsrate

Momentane Änderungsrate

Differentialrechnung

Differenzenquotient

Differentialquotient

Differenzierbarkeit

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .