Hauptsatz der Differential- und Integralrechnung
Du willst wissen, was der Hauptsatz der Differential- und Integralrechnung aussagt und wie man ihn herleitet? Dann bist du hier genau richtig!
Inhaltsübersicht
Hauptsatz der Differential- und Integralrechnung einfach erklärt
Der Hauptsatz der Differential- und Integralrechnung (HDI) führt die Berechnung bestimmter Integrale auf die Berechnung unbestimmter Integrale zurück.
Der Satz lautet: Wenn F(x) eine Stammfunktion der stetigen Funktion f(x) ist, dann gilt
![Rendered by QuickLaTeX.com \[\int_{\textcolor{blue}{a}}^{\textcolor{red}{b}}f(x)dx=[F(x)]_{\textcolor{blue}{a}}^{\textcolor{red}{b}}=F(\textcolor{red}{b})-F(\textcolor{blue}{a}).\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c1f9930a8f7908ffdfc612a7a4fe590a_l3.png)
Du kannst also das bestimmte Integral einer Funktion f berechnen, indem du von dem Funktionswert F(b) der oberen Integralgrenze einer Stammfunktion den Funktionswert F(a) der unteren Integralgrenze subtrahierst.
Übrigens: Der Hauptsatz der Differential- und Integralrechnung setzt die beiden grundlegenden Bereiche der Analysis, also die Differentialrechnung und die Integralrechnung, miteinander in Verbindung. Aus diesem Grund wird er auch Fundamentalsatz der Analysis genannt. Wenn du das vertiefen möchtest, dann schau dir hier unser Video dazu an.
Hauptsatz der Differential- und Integralrechnung — Beweis
Für die Herleitung gehst du davon aus, dass ![Rendered by QuickLaTeX.com f:[\textcolor{blue}{a},\textcolor{red}{b}] \rightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-14efa9c14f7b4737709ca4a97e6f8c0c_l3.png) stetig ist und
stetig ist und ![Rendered by QuickLaTeX.com F:[\textcolor{blue}{a},\textcolor{red}{b}] \rightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e189b38524409aa84cce896201d0a16e_l3.png) mit
mit  die Integralfunktion von f(x) ist. Um den Hauptsatz der Differential- und Integralrechnung herzuleiten, musst du zunächst zeigen, dass der Differentialquotient,
also die Ableitung, existiert und gleich
die Integralfunktion von f(x) ist. Um den Hauptsatz der Differential- und Integralrechnung herzuleiten, musst du zunächst zeigen, dass der Differentialquotient,
also die Ableitung, existiert und gleich  ist.
ist.
![Rendered by QuickLaTeX.com \[\lim_{h\rightarrow 0} \frac{F(\~{x}+h)-F(\~{x})}{h}\stackrel{?}{=}f(\~{x})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ede7afae70f14405b2759ab5f1bbb378_l3.png)
![Rendered by QuickLaTeX.com \~{x}\in[\textcolor{blue}{a},\textcolor{red}{b}]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d60c60bf61e140c25c66edaf84634974_l3.png) fest, aber beliebig und
fest, aber beliebig und  mit
mit ![Rendered by QuickLaTeX.com \~{x}+h\in[\textcolor{blue}{a},\textcolor{red}{b}]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a2de727b37fba93202a559c81a0a8cfe_l3.png) .
.
Wegen der Additivität der Grenzen des Integrals kannst du den Differenzquotient umbauen:
![Rendered by QuickLaTeX.com \[\frac{\textcolor{orange}{F(\~{x}+h)}-\textcolor{teal}{F(\~{x})}}{h}=\frac{1}{h}\biggl( \textcolor{orange}{\int_c^{\~{x}+h}f(t)dt}-\textcolor{teal}{\int_c^{\~{x}}f(t)dt} \biggr)=\frac{1}{h}\int_{\~{x}}^{\~{x}+h}f(t)dt\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3f2d68f3579c8b42b98006da0bc128a9_l3.png)
Der Mittelwertsatz der Integralrechnung
besagt dann, dass es eine reelle Zahl ![Rendered by QuickLaTeX.com \textcolor{magenta}{\xi_h} \in [\~{x},\~{x}+h]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-167b3683f6d99a24bf009432cdf618c4_l3.png) gibt, für die Folgendes gilt:
gibt, für die Folgendes gilt:
![Rendered by QuickLaTeX.com \[ \int_{\~{x}}^{\~{x}+h}f(t)dt=h \cdot f(\textcolor{magenta}{\xi_h})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7224eebb6b8a6c25adbfb097f7cf39f6_l3.png)
Wenn h jetzt gegen 0 geht, wird der Abstand zwischen  und
und  natürlich immer kleiner. Da aber
natürlich immer kleiner. Da aber  noch zwischen
noch zwischen  und
und  liegt, hast du
liegt, hast du  . Für den Grenzwert
. Für den Grenzwert
 gilt also
gilt also 
Wenn du das alles jetzt zusammenfügst, erhältst du:

Du siehst also, dass die Ableitung
von F in  existiert und auch den Wert
existiert und auch den Wert  besitzt. Dass du f und den Limes vertauschen darfst, liegt hierbei übrigens an der Stetigkeit
von f.
besitzt. Dass du f und den Limes vertauschen darfst, liegt hierbei übrigens an der Stetigkeit
von f.
Somit hast du auch bewiesen, dass die Integralfunktion
 eine Stammfunktion
von f ist — sie ergibt nämlich abgeleitet wieder die Funktion f. Und da
eine Stammfunktion
von f ist — sie ergibt nämlich abgeleitet wieder die Funktion f. Und da  gilt können wir außerdem schließen, dass
gilt können wir außerdem schließen, dass
![Rendered by QuickLaTeX.com \[\int_{\textcolor{blue}{a}}^{\textcolor{red}{b}} f(x)dx = F(\textcolor{red}{b}) = F(\textcolor{red}{b})-F(\textcolor{blue}{a})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fca8cd4ff4419257ae673752602aa0a2_l3.png)
Jetzt hast du schon bewiesen, dass der Hauptsatz der Differential- und Integralrechnung für die Integralfunktion gilt. Das ist aber nur eine von vielen Stammfunktionen.
Um den Satz allgemein zu zeigen, müssen wir uns den Unterschied zwischen verschiedenen Stammfunktionen anschauen.
Eine beliebige Stammfunktion  unterscheidet sich von F nur durch eine Konstante. Somit gibt es einen Wert
unterscheidet sich von F nur durch eine Konstante. Somit gibt es einen Wert  mit
mit 
Es gilt also:
![Rendered by QuickLaTeX.com \[\int_{\textcolor{blue}{a}}^{\textcolor{red}{b}} f(t) dt = F(\textcolor{red}{b})-F(\textcolor{blue}{a}) = (\~{F}(\textcolor{red}{b})+C)- (\~{F}(\textcolor{blue}{a})+C) = \~{F}(\textcolor{red}{b}) - \~{F}(\textcolor{blue}{a}) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-50fede2b0dddbde0df5346a77d649b00_l3.png)
Der Hauptsatz der Differential- und Integralrechnung gilt also für alle Stammfunktionen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Eine weitere Variante
Du kannst auch eine andere Darstellung vom HDI verwenden.
Für eine stetige Funktion f ist die Ableitung der Integralfunktion gleich der Integrandenfunktion an der oberen Integralgrenze. Das heißt, es gilt:
![Rendered by QuickLaTeX.com \[\textcolor{orange}{F'(x)}=\frac{d}{dx}\int_{\textcolor{blue}{a}}^{\textcolor{red}{x}} \textcolor{olive}{f(s)}ds=f(\textcolor{red}{x})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b14b88e81e9139a265f31c046a8a0130_l3.png)
An dieser Variante kannst du sehr gut erkennen, dass es unendlich viele Stammfunktionen F(x) einer Funktion f(x) gibt, da die Gleichung für jedes beliebige  gilt.
gilt.
Die Stammfunktionen unterscheiden sich dabei nur in einer einzigen Konstante. Wenn C also eine reelle Zahl
ist, dann, ist  eine Stammfunktion von f.
eine Stammfunktion von f.
Merke: Die erste Variante vom HDI befasst sich mit dem Integral einer Ableitung, bzw. dem Integral von f(x). Die zweite Variante befasst sich hingegen mit der Ableitung eines Integrals.
Damit zeigt der Hauptsatz der Differential- und Integralrechnung auch, dass sich die Ableitung und das Integral gegenseitig umkehren.
Äquivalenz der Varianten
Um zu zeigen, dass die beiden Varianten vom Hauptsatz der Differential- und Integralrechnung tatsächlich äquivalent sind, musst du eine Variante aus der jeweils anderen folgern.
1. Richtung: Variante 1 ⇒ Variante 2
Du weißt schon, dass 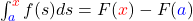 gilt. Du willst jetzt zeigen:
gilt. Du willst jetzt zeigen:  . Dafür setzt du einfach die erste Variante in die linke Seite der zweiten Variante ein.
. Dafür setzt du einfach die erste Variante in die linke Seite der zweiten Variante ein.
Aus  wird also
wird also  .
.
Jetzt kannst du mithilfe der Ableitungsregeln
für Differenzen F(x) und F(a) jeweils einzeln ableiten. Da du nach x ableitest, ist die Ableitung von F(a) dabei 0.
Es bleibt also übrig:
![Rendered by QuickLaTeX.com \[\frac{d}{dx} \int_{\textcolor{blue}{a}}^{\textcolor{red}{x}} f(s)ds=\frac{d}{dx}F(\textcolor{red}{x})-\frac{d}{dx}F(\textcolor{blue}{a})=\frac{d}{dx}F(\textcolor{red}{x})-0=\frac{d}{dx}F(\textcolor{red}{x})=f(x)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8fadad29b6780d9ae6febee1c6a37733_l3.png)
Das entspricht der zweiten Variante. Du hast diese Richtung der Äquivalenz also bewiesen.
2. Richtung: Variante 2 ⇒ Variante 1
Es fehlt noch die andere Richtung, bei der wir von der zweiten Variante ausgehen.
Du setzt dann voraus, dass  gilt. Das heißt, dass die Funktion
gilt. Das heißt, dass die Funktion  eine Stammfunktion von f ist. Entsprechend kannst du das in die erste Variante einsetzen. Du kannst hier dann
eine Stammfunktion von f ist. Entsprechend kannst du das in die erste Variante einsetzen. Du kannst hier dann  und
und  ersetzen.
ersetzen.
Es gilt also:
![Rendered by QuickLaTeX.com \[F(\textcolor{red}{b})-F(\textcolor{blue}{a}) = \int_c^{\textcolor{red}{b}} f(s)ds-\int_c^{\textcolor{blue}{a}} f(s)ds\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dac200788ff30895ee4332f89f67c61a_l3.png)
Jetzt fehlt nur noch ein Schritt. Da wir das Integral von c bis b ausrechnen und schließlich das Integral von c bis a abziehen, bleibt nur das Integral von a bis b übrig. Du kannst also stattdessen direkt dieses Integral verwenden.
![Rendered by QuickLaTeX.com \[\int_c^{\textcolor{red}{b}} f(s)ds - \int_c^{\textcolor{blue}{a}} f(s)ds = \int_{\textcolor{blue}{a}}^{\textcolor{red}{b}} f(s)ds\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3b500f15526c149446f1b165fd0778f3_l3.png)
Wenn wir diese beiden Schritte zusammenfassen, kommst du also zu:
![Rendered by QuickLaTeX.com \[F(\textcolor{red}{b})-F(\textcolor{blue}{a}) = \int_{\textcolor{blue}{a}}^{\textcolor{red}{b}} f(s)ds\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c231adfc3523806792fd33d33eb5bdba_l3.png)
Das entspricht der ersten Variante. Du hast die Aussage jetzt aus beiden Richtungen bewiesen. Die Varianten sind also äquivalent.
Beispiele
Schau dir gleich ein Beispiel an, in dem du den Hauptsatz der Differential- und Integralrechnung anwenden kannst.
Rechne das folgende Integral aus:
![Rendered by QuickLaTeX.com \[\int_{\textcolor{blue}{1}}^{\textcolor{red}{3}} (x^3 -2x) dx\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3ccb408b1893b23d9d7450c2202078ed_l3.png)
Das löst du in 3 einfachen Schritten:
- Ermittle das unbestimmte Integral, also die Stammfunktion.
![Rendered by QuickLaTeX.com \[F(x)=\int (x^3 -2x)dx = \frac{1}{4}x^4 -x^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5a687fe01f04799cedc3f6a7d3119854_l3.png)
- Berechne die Werte für F(a) und F(b), indem du die untere und obere Integrationsgrenze einsetzt, also 1 und 3.
![Rendered by QuickLaTeX.com \[F(\textcolor{blue}{a})=F(\textcolor{blue}{1})=\frac{1}{4}-1=-0,75 \qquad ; \qquad F(\textcolor{red}{b})=F(\textcolor{red}{3})=\frac{81}{4}-9=11,25\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ce6725a5bac8bb7f828ba8d167bedddc_l3.png)
- Bilde die Differenz von F(b) und F(a)
![Rendered by QuickLaTeX.com \[F(\textcolor{red}{b})-F(\textcolor{blue}{a})=F(\textcolor{red}{3})-F(\textcolor{blue}{1})=11,25 - (-0,75) =12\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eb7cd5a54cb5b5f5ab9a52eb842332f8_l3.png)
Übrigens: Die reelle Konstante C musst du hier nicht berücksichtigen, da sie beim Subtrahieren ohnehin wegfallen würde.
Hauptsatz der Differential- und Integralrechnung — häufigste Fragen
(ausklappen)
Hauptsatz der Differential- und Integralrechnung — häufigste Fragen
(ausklappen)-
Was sagt der Hauptsatz der Differential- und Integralrechnung aus?Der Hauptsatz der Differential- und Integralrechnung sagt: Ein bestimmtes Integral ist die Differenz von Stammfunktionswerten. Konkret gilt für eine stetige Funktion
 und eine Stammfunktion
und eine Stammfunktion  :
:  . So wird Integralrechnen auf Stammfunktionen zurückgeführt.
. So wird Integralrechnen auf Stammfunktionen zurückgeführt.
-
Wie berechne ich ein bestimmtes Integral mit einer Stammfunktion?Ein bestimmtes Integral berechnest du, indem du eine Stammfunktion
 bildest und
bildest und  ausrechnest. Dazu setzt du zuerst die obere Grenze
ausrechnest. Dazu setzt du zuerst die obere Grenze  in
in  ein und dann die untere Grenze
ein und dann die untere Grenze  und subtrahierst. Beispiel:
und subtrahierst. Beispiel:  .
.
-
Warum muss f auf dem Intervall stetig sein?
 muss stetig sein, damit im Beweis der Grenzübergang funktioniert und
muss stetig sein, damit im Beweis der Grenzübergang funktioniert und  gilt. Nur dann darfst du den Limes in
gilt. Nur dann darfst du den Limes in  „hineinziehen“ und erhältst am Ende
„hineinziehen“ und erhältst am Ende  .
.
-
Wie entsteht im Beweis das Integral von x bis x plus h?Das Integral von
 bis
bis  entsteht durch die Additivität der Integralgrenzen beim Differenzquotienten. Aus
entsteht durch die Additivität der Integralgrenzen beim Differenzquotienten. Aus  wird deshalb
wird deshalb  .
.
-
Was ist der Unterschied zwischen den zwei Varianten des Hauptsatzes?Die erste Variante berechnet ein bestimmtes Integral über Stammfunktionen:
 . Die zweite Variante beschreibt die Ableitung einer Integralfunktion:
. Die zweite Variante beschreibt die Ableitung einer Integralfunktion:  . Damit sieht man: Integral und Ableitung heben sich gegenseitig auf.
. Damit sieht man: Integral und Ableitung heben sich gegenseitig auf.
Bestimmtes und unbestimmtes Integral
Jetzt weißt du, was der Hauptsatz der Differential- und Integralrechnung aussagt, wie man ihn herleitet und wie man die Äquivalenz seiner Varianten beweist. Du willst dich noch genauer damit auskennen, was der Unterschied zwischen einem bestimmten und unbestimmten Integral ist? Dann schau dir am besten gleich unser Video zu diesem Thema an.

