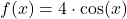Ableitung Cosinus
In diesem Artikel und im Video zeigen wir dir die einfache Cosinus Ableitung und viele Beispiele mit der Kettenregel.
Inhaltsübersicht
Ableitung Cos einfach erklärt
Die Ableitung des Cosinus kannst du dir so merken: Die Cosinus Ableitung ist Minus Sinus.

Am Ableitungskreis siehst du, wie die Ableitungen von Cosinus und Sinus zusammenhängen. Um cos(x) ableiten zu können, musst du dir also nur diesen Zusammenhang merken.
Cos Ableitung mit Kettenregel
Aufwändiger wird es, wenn anstatt nur x ein komplizierterer Ausdruck in cos(x) steht, wie zum Beispiel bei  , und du davon die Ableitung cos berechnen möchtest. In so einem Fall musst du für die Ableitung von cos die Kettenregel
anwenden.
, und du davon die Ableitung cos berechnen möchtest. In so einem Fall musst du für die Ableitung von cos die Kettenregel
anwenden.
Das heißt, du identifizierst die innere Funktion  und die äußere Funktion
und die äußere Funktion  der verketteten Funktion
der verketteten Funktion

Anschließend bestimmst du deren Ableitungen  und
und  und setzt sie zusammen mit
und setzt sie zusammen mit  in die Formel der Kettenregel ein.
in die Formel der Kettenregel ein.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Cos Ableitung — Beispiel 1
Um die Ableitung cos der erwähnten Funktion

zu berechnen, bestimmst du also
-
innere Funktion h(x) und Ableitung h'(x):

-
äußere Funktion g(x) und Ableitung g'(x):

Dabei hast du für die innere Ableitung die Potenz- und Faktorregel angewandt.
Nun setzt du die Ableitungen  und
und  zusammen mit
zusammen mit  in die Formel der Kettenregel ein:
in die Formel der Kettenregel ein:

Damit hast du bereits den cos abgeleitet.
Cos Ableitung — Beispiel 2
Sehen wir uns ein weiteres Beispiel zum cos Ableiten an, nämlich

Für die Berechnung der  Ableitung musst du ebenfalls die Kettenregel
anwenden. Das bedeutet, du bestimmst erneut:
Ableitung musst du ebenfalls die Kettenregel
anwenden. Das bedeutet, du bestimmst erneut:
-
innere Funktion h(x) und Ableitung h'(x):

-
äußere Funktion g(x) und Ableitung g'(x):

Setzt du deine Ergebnisse nun wieder in die Formel der Kettenregel ein, liefert dir das:

Ableitung cos Beispiele
Bisher hast du, wie zum Beispiel beim  Ableiten, lediglich die Kettenregel und die Potenz- und Faktorregel verwendet. Allerdings kann es auch vorkommen, dass du noch weitere Ableitungsregeln benötigst, um eine Funktion mit Cosinus ableiten zu können. Dafür haben wir dir in der folgenden Tabelle eine Reihe solcher Beispiele zur Ableitung cos zusammengefasst:
Ableiten, lediglich die Kettenregel und die Potenz- und Faktorregel verwendet. Allerdings kann es auch vorkommen, dass du noch weitere Ableitungsregeln benötigst, um eine Funktion mit Cosinus ableiten zu können. Dafür haben wir dir in der folgenden Tabelle eine Reihe solcher Beispiele zur Ableitung cos zusammengefasst:
| Ableitungsregel | Funktion | Ableitung |
| Summenregel |

|

|
| Differenzregel |

|

|
| Produktregel |

|

|
| Quotientenregel |

|
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png)
|
| Faktorregel |
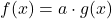
|

|
| Potenzregel |

|
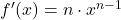
|
Ableitungen trigonometrischer Funktionen
Neben der Ableitung cos x gibt es noch einige andere Funktionen, deren Ableitungen du dir ebenfalls gut einprägen solltest:
| Funktion | Ableitung | |
| Ableitung Sinus |  |
 |
| Ableitung Cosinus |  |
 |
| Ableitung Tangens |  |
 |
Ableitung cos Herleitung
Anstatt dir die Ableitung cos(x) zu merken, kannst du sie dir auch herleiten. Dafür nutzt du folgenden Zusammenhang:  .
.
Statt der Cosinusfunktion benutzt du also die äquivalente Funktion  . Die Sinusfunktion leitest du jetzt mit der Kettenregel ab.
. Die Sinusfunktion leitest du jetzt mit der Kettenregel ab.
-
innere Funktion h(x) und Ableitung h'(x):
 und
und 
-
äußere Funktion g(x) und Ableitung g'(x):
 und
und 
Die Ableitungen h'(x) und g'(x) setzt du jetzt mit h(x) in die Formel der Kettenregel ein:

Merke: Die Cosinusfunktion ist im ganzen Definitionsbereich differenzierbar. Ihre Ableitung ist f'(x)= −sin (x).
Ableitung Cosinus — häufigste Fragen
(ausklappen)
Ableitung Cosinus — häufigste Fragen
(ausklappen)-
Wie merke ich schnell, was bei einer Cosinus-Ableitung die innere Funktion ist?Die innere Funktion ist immer der gesamte Ausdruck in den Klammern von cos(…). Das liegt daran, dass cos(…) die äußere Funktion ist und alles, was du dort einsetzt, als u(x) zählt. Zum Beispiel ist bei cos(4x²+2x) die innere Funktion u(x)=4x²+2x.
-
Welche Fehler passieren am häufigsten beim Ableiten von cos(…) mit der Kettenregel?Am häufigsten fehlt das Minus oder die innere Ableitung u'(x) wird vergessen. Denn korrekt ist immer
 . Außerdem wird u(x) manchmal fälschlich zu sin(x) statt zu sin(u(x)) eingesetzt, also die Klammer ignoriert.
. Außerdem wird u(x) manchmal fälschlich zu sin(x) statt zu sin(u(x)) eingesetzt, also die Klammer ignoriert.
-
Wie leite ich cos(x) ab, wenn im Argument ein Minus steht wie bei cos(−x)?Du leitest
 mit der Kettenregel zu
mit der Kettenregel zu  ab. Denn
ab. Denn  und für u(x)=-x gilt u'(x)=-1, also
und für u(x)=-x gilt u'(x)=-1, also  .
.
-
Wie leite ich cos(u(x)) ab, wenn u(x) selbst eine Wurzel oder ein Bruch ist?Du leitest zuerst außen ab und multiplizierst dann mit der Ableitung der Wurzel oder des Bruchs. Konkret:
 . Beispiel: Für
. Beispiel: Für  ist
ist  , also
, also  .
.
-
Wie unterscheide ich beim Ableiten zwischen cos²(x) und cos(x²)?
 bedeutet
bedeutet  , bei
, bei  steht das Quadrat im Argument. Deshalb ist
steht das Quadrat im Argument. Deshalb ist  , aber
, aber  .
.
Ableitung bestimmter Funktionen
Die Funktion cos(x) kannst du jetzt ableiten! Daneben gibt es noch andere besondere Funktionen wie Wurzelfunktionen, den ln oder e-Funktionen. Wie du diese ableiten kannst, erfährst du im nächsten Beitrag .