Selection Sort
Du fragst dich, wie der Selection Sort funktioniert? Genau das erklären wir dir mit Hilfe eines ausführlichen Beispiels. Im Anschluss zeigen wir dir noch wie sich der Sortieralgorithmus als Pseudocode und Struktogramm aufbauen lässt. Noch dazu kannst du hier die wichtigsten Punkte zu seiner Komplexität erfahren. Am Ende unseres Beitrags findest du noch einen beispielhaften Selection Sort Javacode.
Inhaltsübersicht
Grundidee
Das Sortierverfahren gehört in der Informatik zu den einfachen und instabilen Sortieralgorithmen . Er kann dir auch durch die Begriffe Selectsort oder Exchange Sort bekannt sein.
Das Allgemeine Prinzip kannst du dir als „Sortieren durch Auswahl“ merken. Und das geht in genau zwei Richtungen. Entweder sucht man dabei immer das kleinste (MinSort) oder das größte Element (MaxSort). Das Vorgehen dabei bleibt immer gleich.
Optimized Selection Sort Algorithm
Eventuell stößt du auch mal auf den Begriff „Optimized Selection Sort Algorithm“ – kurz OSSA genannt. Dabei handelt es sich um einen alternativen Ansatz des Selectionsorts. Dabei werden beide Optionen der Sortierung gleichzeitig angewendet, heißt also, dass der MinSort und Maxsort parallel, gemeinsam arbeiten. Entsprechend werden dabei dann immer das größte und kleinste Element in der unsortierten Liste gesucht und entsprechend nach vorne oder nach hinten eingesetzt werden. Dadurch kann im Normalfall eine Beschleunigung erreicht werden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Selection Sort Beispiel
Jetzt schauen wir uns ein auführliches Beispiel eines Standard-Selectionsorts an.
Gegeben sind fünf Spielkarten [7][5][2][9][4] unsortiert in einer Reihe, die der Größe nach aufsteigend nach dem MinSort-Prinzip geordnet werden sollen. Man sieht dabei im ersten Schritt erstmal alle Karten der Reihe nach an und sucht dann nach der Karte mit dem niedrigsten Wert – in diesem Fall die 2. Die 2 wird dann mit der ersten Stelle des unsortierten Bereichs, also der 7, vertauscht. Die Karte 2 ist damit auf ihrem richtigen Platz und gilt als fertigsortiert, deshalb wird sie im weiteren Verlauf nicht mehr beachtet. Nun zum zweiten Wert – der 5, welcher mit der 7, der 9 und der 4 verglichen wird. Die 4 ist kleiner als die 5 und wird deshalb wieder mit der 5 vertauscht. Der Vorgang wird mit der der Karte 7 wiederholt, die dann ihren Platz mit der 5 wechselt und zum Schluss werden auch noch die Karten 9 und 7 ausgetauscht. Am Ende erhält man den fertig sortierte Array: [2][4][5][7][9]
Liste.
Im Folgeden wird der Sortiervorgang des Beispiels anhand der einzelnen Durchläufe dargestellt:
[7][5][2][9][4]
[2][5][7][9][4]
[2][4][7][9][5]
[2][4][5][9][7]
[2][4][5][7][9]
Algorithmus
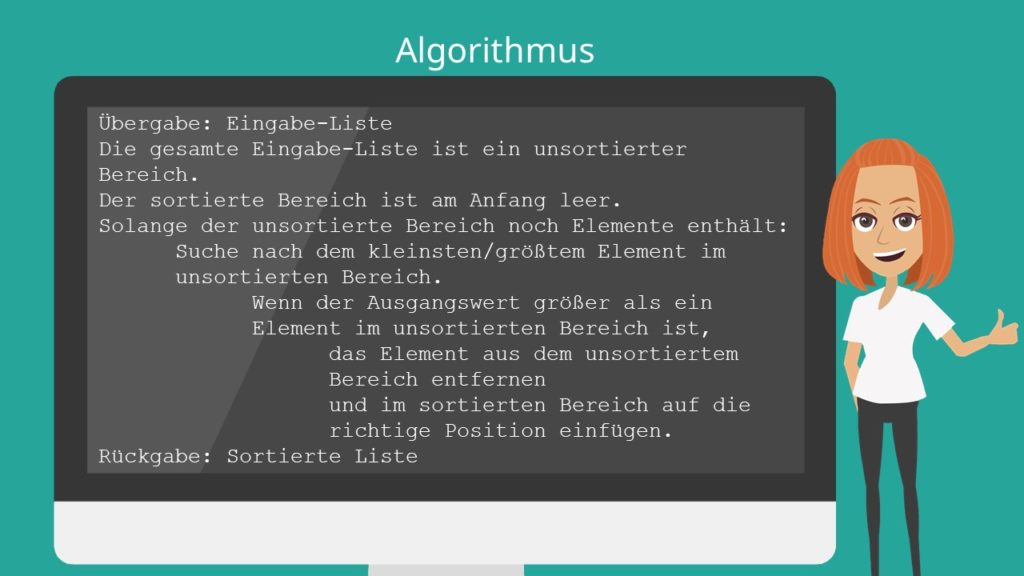
Wir wissen nun also, wie der Sortieralgorithmus funktioniert. Doch was für ein Algorithmus lässt sich daraus jetzt eigentlich ableiten?
Zuerst brauchen wir eine Liste. Diese ist anfangs komplett unsortiert, weswegen der sortierte Bereich zu Beginn als leer gilt. Die Bedingung ist dabei, dass solange der unsortierte Bereich noch ein Element enthält, soll nach dem kleinsten oder dem größten Element im unsortierten Bereich gesucht werden. Sollte ein Element des unsortierten Bereichs kleiner als der Vergleichswert sein, dann wird das passende Element aus dem unsortierten Bereich entfernt und in den Sortierten Bereich an seine richtige Position eingefügt. Am Ende erhalten wir dann eine sortierte Liste.
Hier kannst du dir den theoretischen Aufbau noch einmal genauer ansehen:
Selection Sort Pseudocode
Der Selection Sort Pseudocode lässt sich dann beispielsweise so darstellen:
Selectionsort (Liste l)
For i = 0 to n-2
Do
Minimum = i
For j = i + 1 to n-1
Do
If l[Minimum] > l[j] then Minimum = j
tmp = l[i]
l[i] = l[Minimum]
l[Minimum] = tmpSelection Sort Struktogramm
Zusätzlich kannst du den Pseudocode natürlich auch als Selection Sort-Struktogramm darstellen. Das könnte dann beispielsweise so aussehen:
Selection Sort Laufzeit
Doch wie sieht es jetzt noch mit der Laufzeitkomplexität aus? Der Sortieralgorithmus ist nämlich ein ziemlich besonderer Fall, denn es sind wie beim Mergesort keine Unterschiede festzustellen. Die Laufzeit im Selection Sort Worst Case entspricht genau der Komplexität im Best Case. Damit beträgt die Selection Sort Laufzeit immer O(n2) . Das hat einen ganz einfachen Grund, denn die Liste wird unabhängig von vorsortierten Daten immer von vorne bis hinten komplett durchlaufen. Deshalb benötigt er Vergleiche, wovon wir die allgemeine Selection Sort Laufzeit ableiten können.
Selection Sort Java Code
Zum Abschluss zeigen wir dir auch noch ein Beispiel für einen Quellcode einer Selection Sort Java-Implementierung:
//Liste l, die mit dem Heapsort sortiert werden soll
public class SelectionSort
{
private int[] l;
// Übernehmen von Referenz auf eine Liste und sortiert sie
public void sort(int[] anListe)
{
l=anListe;
Sortierung();
}
// sortiert doe Liste l mit dem Selectionsort
private void Sortierung()
{
for (int i=0; i<l.length-1; i++)
{
int pm = PositionMinimum(i);
swap(pm, i);
}
}
// findet die Position der kleinsten Zahl PositionMinimum ab der ersten Position erste Zahl im unsortierten Bereich
private int PositionMinimum(int ersteZahl)
{
int pm = ersteZahl;
for (int i=ersteZahl+1; i<l.length; i++)
if (l[i]<l[pm])
pm = i;
return pm;
}
// tausche zwei Zahlen in der Liste
private void swap(int i, int j)
{
int tmp=l[i];
l[i]=l[j];
l[j]=tmp;
}
}