Stetigkeit
Die Stetigkeit von Funktionen spielt bei vielen Berechnungen eine Rolle! Hier erfährst du, welche Bedingungen stetige Funktionen erfüllen müssen und wie das Epsilon-Delta-Kriterium funktioniert!
Inhaltsübersicht
Was bedeutet Stetigkeit in Mathe?
Bildlich gesprochen ist eine Funktion stetig, wenn du sie als eine einzelne Linie ohne Absetzen deines Stiftes zeichnen kannst. Mathematischer formuliert findest du die Stetigkeit von Funktionen, indem du den rechtsseitigen Grenzwert mit dem linksseitigen Grenzwert vergleichst.
Um zu beweisen, dass eine Funktion an der Stelle x0 stetig ist, musst du 3 Punkte nachweisen:
- Die Funktion ist an der Stelle x0 definiert: f(x0) existiert.
- Der rechts- und linksseitige Grenzwert sind an der Stelle x0 gleich: Der beidseitige Grenzwert
 existiert.
existiert. - Der Grenzwert ist gleich dem Funktionswert:

Laut Definition der Stetigkeit gilt: Ist die Stetigkeit einer Funktion an jeder Stelle gegeben, handelt es sich um eine stetige Funktion.
Stetigkeit von Funktionen — Rechenregeln
Wenn du zwei stetige Funktionen g(x) und h(x) mit einer der folgenden Rechenoperationen kombinierst, ist auch ihre Kombination f(x) stetig:
- Addition und Subtraktion erhalten die Stetigkeit einer Funktion: f(x) = g(x) + h(x) oder f(x) = g(x) – h(x).
- Multiplikation erhält die Stetigkeit einer Funktion: f(x) = g(x) • h(x).
-
Division erhält die Stetigkeit einer Funktion:
 , wenn
, wenn 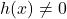 .
. - Verkettung erhält die Stetigkeit einer Funktion: f(x) = g(h(x)).
Manche Funktionen sind immer stetig. Dazu gehören: ganzrationale Funktionen , gebrochenrationale Funktionen , Wurzelfunktionen , trigonometrische Funktionen und ihre Umkehrfunktionen , Exponentialfunktionen und Logarithmusfunktionen .
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
1. Beispiel: Unstetige Funktion
Ist f(x) an der Stelle x0=2 stetig?
![Rendered by QuickLaTeX.com \[ f(x) = \left\{ \begin{array}{ll} -1 & \text{für } x < 2\\ 0 & \text{für } x = 2 \\ 1 & \text{für } x > 2 \end{array} \right \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-02d0ce114ba45d2c05db43042fffdba7_l3.png)
1. Bedingung: Ist die Stelle x0 Teil der Definitionsmenge?
f(x) ist für x = 2 definiert. Die Stelle x0 = 2 ist also Teil der Definitionsmenge. f(x) erfüllt an der Stelle x = 2 die erste Bedingung.
2. Bedingung: Besitzt f(x) einen beidseitigen Grenzwert an der Stelle x0?
Der beidseitige Grenzwert existiert, wenn der rechts- und linksseitige Grenzwert identisch sind. Bestimme also den rechtsseitigen Grenzwert, um die Stetigkeit zeigen zu können!
Weil du dich der Stelle 2 von größeren Zahlen näherst, sind alle Zahlen, die du in deinen Limes einsetzt, größer als 2. Deine Funktion ist für diese Zahlen also immer 1. Deshalb ist auch dein Grenzwert gleich 1.
![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow 2^+} f(x) = \lim_{x\rightarrow 2^+} 1 = \text{1} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-aa133e6aff8347afcb2724530b7d9c4e_l3.png)
Analog rechnest du den linksseitigen Grenzwert aus: Weil du dich der Stelle 2 von kleineren Zahlen näherst, sind alle Zahlen, die du in deinen Limes einsetzt, kleiner als 2. Deine Funktion ist also für diese Zahlen immer -1. Dein Grenzwert ist deshalb gleich -1.
![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow 2^-} f(x) = \lim_{x\rightarrow 2^-} -1 = \text{-1} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-11d014dfd5d31bbabdf6e2992ad4e9e5_l3.png)
Der rechts- und linksseitige Grenzwert sind unterschiedlich. Es existiert kein beidseitiger Grenzwert. f(x) erfüllt also nicht die zweite Bedingung: Sie ist an der Stelle x = 2 unstetig. Also haben wir eine unstetige Funktion.
2. Beispiel: Unstetige Funktion
Die Zuordnung f(x) ist die sogenannte Delta-Distribution. Untersuche ihre Stetigkeit an der Stelle x0 = 0.
![Rendered by QuickLaTeX.com \[ f(x) = \left\{ \begin{array}{ll} 0 & \text{für } x \neq 0 \\ 1 & \text{für } x = 0 \end{array} \right \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-edf58f7ca76e75b943581b52bb7555d8_l3.png)
1. Bedingung: Ist die Stelle x0 Teil der Definitionsmenge?
f(x) ist für x = 0 definiert. 0 ist also Teil der Definitionsmenge. Die erste Bedingung wird von f(x) erfüllt.
2. Bedingung: Besitzt f(x) einen beidseitigen Grenzwert an der Stelle x0?
Der beidseitige Grenzwert existiert, wenn der rechts- und linksseitige Grenzwert identisch sind. Zuerst bestimmst du den rechtsseitigen Grenzwert. Weil du dich der Stelle x = 0 von größeren Zahlen nur näherst, sind alle Zahlen, die du in deine Funktion einsetzt, ungleich 0. Deine Funktion ist also f(x) = 0. Deshalb ist dein Grenzwert gleich 0.
![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow 0^+} f(x) = \lim_{x\rightarrow 0^+} 0 =\tetx{0} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d16841fa930086454986f4089d51efee_l3.png)
Analog rechnest du den linksseitigen Grenzwert aus: Weil du dich der Stelle 0 von kleineren Zahlen nur nährst, sind alle Zahlen, die du in deinen Limes einsetzt, ungleich 0. Deine Funktion ist also wieder f(x) = 0. Dein Grenzwert ist deshalb gleich 0.
![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow 0^-} f(x) = \lim_{x\rightarrow 0^-} 0 = \text{0} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8bdf5d1f9b58bbb28e9847d32ccbb33e_l3.png)
Der rechts- und linksseitige Grenzwert sind identisch. Es existiert ein beidseitiger Grenzwert mit dem Wert 0. Die zweite Bedingung ist also erfüllt.
![Rendered by QuickLaTeX.com \[\lim_{x\rightarrow 0} f(x) = 0\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-85d25b094e709a9b6715f1e8b40bf5ec_l3.png)
3. Bedingung: Sind Grenzwert und Funktionswert an der Stelle x0 gleich?
Wenn du x = 0 in die Funktion f(x) einsetzt, erhältst du den Funktionswert f(0) = 1. Dein beidseitiger Grenzwert ist allerdings gleich 0. Die dritte Bedingung ist nicht erfüllt. f(x) ist an der Stelle x = 0 also nicht stetig.
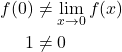
3. Beispiel: Stetige Funktion
Untersuche die Stetigkeit von Funktion g(x) an der Stelle x0 = -1!
![Rendered by QuickLaTeX.com \[ g(x) = x^2 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-70dc3c24b1f419f180bff32cd8e41c3b_l3.png)
1. Bedingung: Ist die Stelle x0 Teil der Definitionsmenge?
g(x) ist eine ganzrationale Funktion. Deshalb gehören alle Zahlen, einschließlich x0, zur Definitionsmenge. Die erste Bedingung, um Stetigkeit zu beweisen, ist erfüllt.
2. Bedingung: Besitzt g(x) einen beidseitigen Grenzwert an der Stelle x0?
Fange wieder mit dem rechtsseitigen Grenzwert an: Wenn du dich der Stelle x = -1 von größeren Zahlen näherst, geht die Parabel g(x) = x2 gegen +1.
![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow -1^+} x^2 = 1 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8486da17d5c40ce973b76aff3655280b_l3.png)
Analog geht der linksseitige Limes gegen +1, wenn du dich der Stelle x = -1 von kleineren Zahlen näherst.
![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow -1^-} x^2 = 1 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d59fa6eebc80ba64a2c911e55c174898_l3.png)
Der rechts- und linksseitige Limes sind also identisch. Der beidseitige Grenzwert existiert also und hat den Wert 1. Die zweite Bedingung ist demnach erfüllt.
![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow -1} x^2 = 1 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-de55e9f1281059d66ddfdbe7b4a4f271_l3.png)
3. Bedingung: Sind Grenzwert und Funktionswert an der Stelle x0 gleich?
Wenn du x = -1 in die Funktion g(x) einsetzt, erhältst du den Funktionswert g(-1) = 1. Dein beidseitiger Grenzwert ist ebenfalls gleich 1. g(x) ist an der Stelle x = -1 also stetig.Tatsächlich handelt es sich bei der Funktion g(x) = x2 um eine stetige Funktion.
![Rendered by QuickLaTeX.com \[ g(-1) = \lim_{x\rightarrow -1} g(x) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8e02843cb88057683588d0b38653cedb_l3.png)
Epsilon-Delta-Kriterium
Der strenge mathematische Beweis von Stetigkeit ist das  –
– -Kriterium (Epsilon-Delta-Kriterium):
-Kriterium (Epsilon-Delta-Kriterium):
![Rendered by QuickLaTeX.com \[ \forall \epsilon > 0 \;\exists\; \delta > 0 \quad \forall x \in D: |x-x_0| < \delta \Rightarrow |f(x)-f(x_0)| < \epsilon \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-29b3e1ae04f5f7d0fd1ed6e8d35fa1db_l3.png)
Ausgeschrieben heißt das: „Für jedes beliebig wählbare Epsilon größer als Null gibt es ein Delta größer als Null. Dann soll für alle x aus dem Definitionsbereich D deiner Funktion f folgende Aussage gelten: Wenn der Abstand zwischen x und x0 kleiner als Delta ist, dann ist auch der Abstand zwischen f(x) und f(x0) kleiner als Epsilon.“
Aber was bedeutet das? Wenn du von zwei Punkten auf deiner stetigen Funktion den Abstand der x-Koordinaten ( ) verkleinerst, muss gleichzeitig der Abstand zwischen den y-Koordinaten (
) verkleinerst, muss gleichzeitig der Abstand zwischen den y-Koordinaten ( ) kleiner werden.
) kleiner werden.
Schau dir das am besten an einem Beispiel an. Ist die Funktion f(x)=x2+1 an der Stelle x0=3 stetig?
Um das zu lösen, suchst du für ein beliebiges  ein spezielles
ein spezielles  , sodass die Bedingung oben für alle x in dieser Deltaumgebung von x0=3 erfüllt ist.
, sodass die Bedingung oben für alle x in dieser Deltaumgebung von x0=3 erfüllt ist.
Sei  . Dann kannst du abschätzen:
. Dann kannst du abschätzen:

Dieses Produkt, das du mit der dritten binomischen Formel
aufgestellt hast, kannst du jetzt mit  abschätzen. Dieses
abschätzen. Dieses  hast du zu diesem Zeitpunkt aber noch nicht konkret bestimmt, du weißt nur, dass gilt:
hast du zu diesem Zeitpunkt aber noch nicht konkret bestimmt, du weißt nur, dass gilt:  .
.

Ziehe die +6 aus den Betragsstrichen heraus, damit du wieder mit  abschätzen kannst. Aber aufgepasst: Das ist keine Äquivalenzumformung, sondern eine Dreiecksungleichung
. Du musst also ein Kleiner-Gleich-Zeichen benutzen!
abschätzen kannst. Aber aufgepasst: Das ist keine Äquivalenzumformung, sondern eine Dreiecksungleichung
. Du musst also ein Kleiner-Gleich-Zeichen benutzen!

Jetzt weißt du also, dass ein  dem Epsilon-Delta-Kriterium genügt und die folgende Bedingung erfüllt:
dem Epsilon-Delta-Kriterium genügt und die folgende Bedingung erfüllt:
![Rendered by QuickLaTeX.com \[ \delta^2 + 6\delta = \epsilon \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9011bf2ea8bc1e96bedeaf1799871ff4_l3.png)
Denn dann würde ja gelten:
![Rendered by QuickLaTeX.com \[ |f(x)-f(3)| < \delta^2 + 6\delta = \epsilon \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8d760156e5fe5192e362d8f50d972c7c_l3.png)
Allerdings hast du erst einen Ausdruck für  . Bilde als nächstes die Umkehrfunktion
mit der pq-Formel
, um
. Bilde als nächstes die Umkehrfunktion
mit der pq-Formel
, um  zu bestimmen.
zu bestimmen.
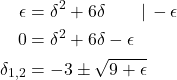
Da  sein muss, setzt du also
sein muss, setzt du also  . Damit hast du ein passendes
. Damit hast du ein passendes  gefunden.
gefunden.
f(x)=x2+1 erfüllt an der Stelle x0=3 also das Epsilon-Delta-Kriterium. f(x) ist damit an der Stelle x0=3 stetig.
Unstetige Funktionen
Schau dir abschließend noch 2 unstetige Funktionen an. Erinnere dich dafür an die Definition von Stetigkeit:
Eine Funktion f(x) ist an einer Stelle x0 stetig, wenn
1.)  definiert ist
definiert ist
und die folgenden zwei Bedingungen erfüllt sind:
2.)  existiert und
existiert und
3.) 
Eine unstetige Funktion, die Bedingung 2.) nicht erfüllt, ist f(x).
![Rendered by QuickLaTeX.com \[ f(x) = \left\{ \begin{array}{ll} x^2 & \text{für } x\leq 1 \\ x+1 & \text{für } x > 1 \end{array} \right \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0447cf901f8146f54be43447a7a42e44_l3.png)
Dagegen ist g(x) eine unstetige Funktion, die Bedingung 3.) nicht erfüllt.
![Rendered by QuickLaTeX.com \[ f(x) = \left\{ \begin{array}{ll} -x^2 +5 & \text{für } x\neq 2 \\ x & \text{für } x = 2 \end{array} \right \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fc4266d40f859d57d2298425b413a365_l3.png)
Stetigkeit — häufigste Fragen
(ausklappen)
Stetigkeit — häufigste Fragen
(ausklappen)-
Wie unterscheide ich Stetigkeit an einer Stelle von Stetigkeit überall?Stetigkeit an einer Stelle
 bedeutet:
bedeutet:  ist definiert und es gilt
ist definiert und es gilt  . Stetigkeit überall bedeutet: Diese Bedingung gilt für jedes
. Stetigkeit überall bedeutet: Diese Bedingung gilt für jedes  im Definitionsbereich. Eine Funktion kann also an vielen Stellen stetig sein und trotzdem einzelne Unstetigkeitsstellen haben.
im Definitionsbereich. Eine Funktion kann also an vielen Stellen stetig sein und trotzdem einzelne Unstetigkeitsstellen haben.
-
Welche typischen Fehler passieren beim Prüfen von Stetigkeit mit Grenzwerten?Typische Fehler sind: Man prüft nur den beidseitigen Grenzwert und vergisst zu kontrollieren, ob
 überhaupt definiert ist. Außerdem werden links- und rechtsseitiger Grenzwert nicht getrennt berechnet. Beispiel: Wenn
überhaupt definiert ist. Außerdem werden links- und rechtsseitiger Grenzwert nicht getrennt berechnet. Beispiel: Wenn  , existiert der beidseitige Grenzwert nicht.
, existiert der beidseitige Grenzwert nicht.
-
Wie finde ich bei einer stückweise definierten Funktion alle Unstetigkeitsstellen?Unstetigkeitsstellen liegen bei stückweise definierten Funktionen fast immer an den Übergangsstellen der Fallunterscheidung und an Stellen, an denen ein Teilstück nicht definiert ist. Prüfe jede Übergangsstelle
 mit
mit  ,
,  und
und  . Beispiel: Stimmen die beiden einseitigen Grenzwerte nicht überein, liegt bei
. Beispiel: Stimmen die beiden einseitigen Grenzwerte nicht überein, liegt bei  eine Sprungstelle vor.
eine Sprungstelle vor.
-
Wie wähle ich beim Epsilon-Delta-Beweis ein sinnvolles Delta aus?Ein sinnvolles
 wählst du, indem du
wählst du, indem du  so abschätzt, dass rechts ein Ausdruck steht, in dem
so abschätzt, dass rechts ein Ausdruck steht, in dem  vorkommt und du dann
vorkommt und du dann  einsetzt. Oft setzt man zusätzlich
einsetzt. Oft setzt man zusätzlich  , um Terme wie
, um Terme wie  nach oben zu begrenzen und am Ende
nach oben zu begrenzen und am Ende  als Funktion von
als Funktion von  zu wählen.
zu wählen.
-
Warum reicht es nicht, dass der Grenzwert existiert?Dass der Grenzwert
 existiert, reicht für Stetigkeit nicht, weil zusätzlich
existiert, reicht für Stetigkeit nicht, weil zusätzlich  definiert sein muss und der Grenzwert genau diesen Funktionswert treffen muss. Beispiel: Existiert der Grenzwert, aber
definiert sein muss und der Grenzwert genau diesen Funktionswert treffen muss. Beispiel: Existiert der Grenzwert, aber  , dann liegt eine hebbare Unstetigkeit vor.
, dann liegt eine hebbare Unstetigkeit vor.
Beidseitiger Grenzwert
Du hast jetzt zwei verschiedene Wege kennengelernt Unstetigkeiten zu finden. Am schnellsten ist dabei die Methode des beidseitigen Grenzwertes. Damit du den immer zuverlässig berechnen kannst, musst du dir unbedingt unser Video dazu anschauen!







