Reelle Zahlen
Es gibt viele verschiedene Arten von Zahlen. Du kannst sie in unterschiedlichen Zahlenmengen zusammenfassen. Hier zeigen wir dir, was du über die Menge der reellen Zahlen wissen musst. Schaue dir auch unser passendes Video an!
Inhaltsübersicht
Was sind reelle Zahlen?
Die Menge der reellen Zahlen enthält alle Zahlen, die du aus der Schule kennst. Sie besteht aus den rationalen Zahlen und den irrationalen Zahlen . Jede irrationale und rationale Zahl ist also gleichzeitig eine reelle Zahl. Aber wann ist eine Zahl irrational?
Eine Zahl ist irrational, wenn du sie nicht als einen Bruch von zwei ganzen Zahlen
schreiben kannst. Umgekehrt kannst du rationale Zahlen immer als einen Bruch von ganzen Zahlen darstellen. Das Zeichen für die Menge der rationalen Zahlen ist 
. Die Zahlen 2 und -3,43 sind zum Beispiel rational:
![\[ 2 = \frac{2}{1} \quad -3,34 = \frac{-334}{10} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4bc8c6ffab164789920383b87b5e5dd2_l3.png "Rendered by QuickLaTeX.com")
Die Wurzel von 2, die Eulersche Zahl e und die Kreiszahl 
sind beispielsweise irrational. Du kannst sie nicht als Bruch schreiben und sie haben unendlich viele Nachkommastellen, die sich nicht wiederholen. Das Zeichen der irrationalen Zahlen ist 
.
![\[ \sqrt{2} = 1,414 1\dots \quad \mathrm{e} = 2,718 \dots \quad \pi = 3,141 5\dots\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-38793b5b9f748727e9e7180b3db89bcf_l3.png "Rendered by QuickLaTeX.com")
Das reellen-Zahlen-Zeichen ist 
und die Menge der reellen Zahlen enthält alle rationalen und irrationalen Zahlen:
![\[ \textcolor{magenta}{\mathbb{R}} = \textcolor{red}{\mathbb{Q}}\cup\textcolor{orange}{\mathbb{I}} = \{ \dots; -3,34; \sqrt{2}; 2; \mathrm{e}; \pi; \dots \} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-bf42f6f9fd650625bb4f701c15d605d3_l3.png "Rendered by QuickLaTeX.com")
Bei den reellen Zahlen musst du auf die Rechtschreibung aufpassen (reelle Zahl, nicht reele Zahl oder reele Zahlen)!
Reelle Zahlen Beispiele
Aber was sind reelle Zahlen? Schaue dir dafür die Zahlengerade oder den Zahlenstrahl an: Reelle Zahlen sind zum Beispiel die natürlichen Zahlen 1, 3, 8 und 129 oder die ganzen Zahlen -33, -25 und -982. Gebrochene Zahlen sind auch reelle Zahlen. Gebrochene Zahlen wie rationale Zahlen (
, -3,25, 
und 5,14) gehören also auch zu den reellen Zahlen. Irrationale Zahlen sind auch gebrochene Zahlen. Beispiele für irrationale Zahlen sind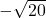 
, 
, e und .
Primzahlen
Eine weitere Menge von Zahlen, die auch zu den reellen Zahlen gehören sind die Primzahlen . Schaue dir gleich unser Video dazu an!
