Chi Quadrat Test
In diesem Beitrag zeigen wir dir, wie du den Chi Quadrat Test problemlos durchführen kannst. Wir erklären dir nicht nur, wie du den Chi Quadrat Test schrittweise durchführen kannst, sondern klären dich auch über wichtige Voraussetzungen auf. Außerdem liefern wir dir anschauliche Chi Quadrat Test Beispiele zum weiteren Verständnis.
Eine visuelle Erläuterung zum Chi Quadrat Test liefert dir unser Lernvideo !
Inhaltsübersicht
Chi Quadrat Test einfach erklärt
Der Chi Quadrat Test ist ein Testverfahren der Statistik, das Aussagen über den Zusammenhang zwischen Variablen treffen kann, die entweder nominal oder ordinal skaliert sind. Beim Chi Quadrat Test handelt es sich zudem um eine Art des Hypothesentests . Per Definition wird er oftmals auch als Chi Quadrat Anpassungstest oder Chi Quadrat Unabhängigkeitstest bezeichnet, da der Test den Zusammenhang der Variablen in Bezug auf die stochastische Unabhängigkeit prüft. Die Darstellung und Berechnung läuft dabei hauptsächlich über die Kreuztabelle. Die genaue Berechnung und konkrete Beispiele liefern wir dir in den folgenden Abschnitten.
Chi Quadrat berechnen
Für die Berechnung des Chi Quadrat Test und den dadurch zu erhaltenden Chi Quadrat Wert gibt es eine allgemein gültige Formel, die folgendermaßen aussieht:

Aus der Formel lässt sich auch direkt die Vorgehensweise für die Berechnung ableiten. Über die Zeilen- und Spaltensummen berechnest du im ersten Schritt die erwarteten Häufigkeiten für jede Zelle deiner Kreuztabelle, damit du im Anschluss zusammen mit den beobachteten Häufigkeiten nach der Formel vorgehen kannst und für jede Zelle Werte berechnest, die du zum Schluss zum endgültigen Chi Quadrat Wert aufsummierst. Der berechnete Chi Quadrat Wert muss am Ende im Zuge der Interpretation noch an einem kritischen Wert getestet werden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Chi Quadrat Test Voraussetzungen
Die Hauptvoraussetzung für die Durchführung eines Chi Quadrat Test ist das passende Skalenniveau. Die betrachteten Variablen sollten daher entweder nominales oder ordinales Skalenniveau aufweisen. Außerdem sollte die Stichprobengröße bzw. die Fallzahl bei über 50 Personen liegen. Das liegt daran, dass eine Zelle keine erwartete Häufigkeit kleiner 5 annehmen sollte. Ansonsten würde der Chi Quadrat Test keine validen Ergebnisse produzieren. Je kleiner die Fallzahl ist, desto eher würde ein solches Szenario eintreten. In solchen Fällen ist es dann sinnvoller, den sogenannten exakten Test nach Fisher anzuwenden.
Chi Quadrat Test Beispiel
Anhand zweier verschiedener Beispiele soll jetzt die gerade eben erklärte Vorgehensweise anschaulich gemacht werden. Wir arbeiten dabei im ersten Beispiel mit zwei nominalskalierten Variablen und einer 2×2-Kreuztabelle und im zweiten Beispiel mit zwei ordinalskalierten Variablen und einer 3×3-Kreuztabelle.
Berechnung mit nominal skalierten Variablen
Wir starten mit dem Beispiel, in dem wir den Zusammenhang zwischen den beiden nominalen Variablen Geschlecht und Spielen eines Instruments anhand des Chi Quadrat Test überprüfen wollen. Dafür gehen wir davon aus, dass in einer Erhebung 100 Grundschulkinder befragt wurden. Die Ergebnisse werden anschließend gruppiert in einer Kreuztabelle festgehalten.
| spielt Instrument | spielt kein Instrument | Summe | |
| männlich | 23 | 29 | 52 |
| weiblich | 38 | 10 | 48 |
| Summe | 61 | 39 | 100 |
In der letzten Spalte sowie der letzten Zeile werden außerdem jeweils die Spalten- und Zeilensummen festgehalten, die man für den ersten Schritt der Berechnung des Chi Quadrat Werts unbedingt benötigt. In diesem ersten Schritt wird nun für jede Zelle der Kreuztabelle die zugehörige erwartete Häufigkeit berechnet. Dafür musst du einfach die Spalten- und Zeilensumme der betrachteten Zelle miteinander multiplizieren und anschließend durch die Fallzahl dividieren, die du ebenfalls ganz unten rechts in der Tabelle vermerkt hast. Zur Veranschaulichung des Vorgangs siehst du hier die ausgeschriebene Formel zur Berechnung der erwarteten Wahrscheinlichkeit:
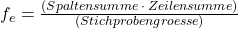
Führst du diese Berechnung nun für alle vier Zellen deiner 2×2 Kreuztabelle durch, dann erhältst du diese Ergebnisse:




Bei einer Verteilung nach den erwarteten Häufigkeiten würde absolut kein Zusammenhang zwischen den beiden Variablen bestehen.
Um den Überblick über deine zusammengehörenden Werte zu behalten, vermerkst du die eben berechneten erwarteten Häufigkeiten neben den bereits eingetragenen beobachteten Häufigkeiten in der Tabelle.
| spielt Instrument | spielt kein Instrument | Summe | |
| männlich | 23 | 31,72 | 29 | 20,28 | 52 |
| weiblich | 38 | 29,28 | 10 | 18,72 | 48 |
| Summe | 61 | 39 | 100 |
Du kannst zwar noch keine endgültige Aussage über das Verhältnis der Variablen zueinander treffen bevor die vollständige Berechnung abgeschlossen ist, jedoch lassen sich bereits auf den ersten Blick an einigen Stellen deutliche Abweichungen erkennen. Diese bieten zumindest einen ersten numerischen Anhaltspunkt dafür, dass du hier möglicherweise einen Zusammenhang zwischen den Variablen nachweisen kannst.
Chi Quadrat Wert
Im nächsten Schritt kommt bereits die Formel des Chi Quadrat Test, die du vorhin schon kennengelernt hast, zum Einsatz. Durch die Berechnung der erwarteten Häufigkeiten für alle Zellen hast du nämlich bereits alle notwendigen Werte zusammen. Konkret werden jetzt für jede Zelle die Differenzen zwischen der beobachteten und der erwarteten Häufigkeit gebildet, anschließend quadriert und dann durch die erwartete Häufigkeit dividiert. Die Ergebnisse für die einzelnen Zellen werden dann in einem letzten Schritt zum Chi Quadrat Wert aufsummiert.
Zur Erinnerung siehst du hier nochmals die Formel:

Du führst nun für jede Zelle einzeln die Berechnung durch, die der Bruch der Formel vorgibt. Das sieht dann für die jeweiligen Zellen folgendermaßen aus:




Nun müssen die einzelnen Ergebnisse nur noch aufsummiert werden, um den Chi Quadrat Wert zu erhalten.
Chi Quadrat = 2,40 + 3,75 + 2,60 + 4,06 = 12,81
Wie du den Chi Quadrat Wert verwenden kannst, um schlussendlich Aussagen über den Zusammenhang zwischen deinen Variablen treffen zu können, erfährst du im Kapitel zur Interpretation von Chi Quadrat. Du kannst dir aber auf jeden Fall merken, dass mit der Berechnung des Chi Quadrat Werts nur der erste Teil des Chi Quadrat Test abgeschlossen ist.
Bevor also in die weitere Verwendung des Chi Quadrat Wertes und seine anschließende Interpretation eingetaucht wird, betrachten wir der Vollständigkeit halber noch ein zweites Beispiel, da der Chi Quadrat Test auch an ordinalen Variablen durchgeführt werden kann.
Berechnung mit ordinal skalierten Variablen
Im zweiten Beispiel zum Chi Quadrat Test arbeiten wir nun mit zwei Variablen mit ordinalem Skalenniveau, die sich in einer 3×3-Kreuztabelle darstellen lassen. Es soll dabei über den Chi Quadrat Test der Zusammenhang zwischen Schulabschluss und Einkommen geprüft werden. Bei den Schulabschlüssen wird dabei zwischen den Kategorien Hauptschulabschluss, mittlere Reife und (Fach-)Abitur unterschieden. Für das Einkommen werden drei verschiedene Stufen gebildet: Stufe I: 0€ – 30.000€, Stufe II: 30.001€ – 60.000€ und Stufe III: 60.001€ – 100.000€. Befragt wurden daher in einer fiktiven Befragung Personen, die einen dieser Schulabschlüsse besitzen und zwischen 0€ und maximal 100.000€ jährlich verdienen. In der Kreuztabelle lassen sich all diese Informationen dann wieder folgendermaßen darstellen:
| Schulabschluss\Einkommen | 0 – 30.000 € | 30.001 € – 60.000 € | 60.001 € – 100.000 € | Summe |
| Hauptschulabschluss | 39 | 40 | 13 | 92 |
| Mittlere Reife | 22 | 48 | 17 | 87 |
| Abitur | 11 | 66 | 44 | 121 |
| Summe | 72 | 154 | 74 | 300 |
Wie bereits im ersten Beispiel, berechnest du auch hier mithilfe der Spalten- und Zeilensummen sowie der gesamten Fallzahl die erwarteten Häufigkeiten für jede einzelne Zelle.









Überträgst du jetzt wie auch im ersten Beispiel alle erwarteten Häufigkeiten ebenfalls in die Tabelle, ergibt sich folgende Situation:
| Schulabschluss\Einkommen | 0 – 30.000 € | 30.001 € – 60.000 € | 60.001 € – 100.000 € | Summe |
| Hauptschulabschluss | 39 | 22,08 | 40 | 47,23 | 13 | 22,70 | 92 |
| Mittlere Reife | 22 | 20,88 | 48 | 44,66 | 17 | 21,46 | 87 |
| Abitur | 11 | 29,04 | 66 | 62,11 | 44 | 29,85 | 121 |
| Summe | 72 | 154 | 74 | 300 |
Jetzt führst du die Berechnung der Formel wieder an jeder einzelnen Zelle durch, sodass du am Schluss alles zum gesamten Chi Quadrat Wert und somit deinem Ergebnis aufsummieren kannst.










Der Chi Quadrat Wert für deine Kreuztabelle mit den zugrunde liegenden Variablen Schulabschluss und Einkommen beträgt also 37,63.
Anhand beider Beispiele erfährst du im folgenden Abschnitt nun genau, wie du den Chi Quadrat Wert im Zuge des Chi Quadrat Test weiter verwendest und in diesem Zusammenhang mit der Chi Quadrat Verteilungstabelle arbeitest.
Chi Quadrat Test Interpretation
Nachdem du jetzt für zwei verschiedene Beispiele jeweils den Chi Quadrat Wert berechnet hast, fragst du dich sicher, inwiefern dir dieser jetzt dabei helfen soll, eine Aussage über den Zusammenhang zwischen den betrachteten Variablen zu treffen. Das Vorzeichen und die Höhe des Chi Quadrat Werts allein besitzen tatsächlich keine Aussagekraft über seine Richtung oder seine Stärke. Du könntest daher auf Basis des Werts nicht behaupten, dass das Geschlecht und das Spielen eines Instruments mit einem Chi Quadrat Wert von 12,81 weniger stark zusammenhängen als Schulabschluss und Einkommen mit einem Chi Quadrat Wert von 37,63. Daher kommt jetzt der zweite Teil des Chi Quadrat Test zum Einsatz.
Chi Quadrat Freiheitsgrade
Es muss nämlich beim Chi Quadrat Test wie auch bei anderen Hypothesentests (z.B. dem t Test ) mithilfe des Signifikanzniveaus und den Freiheitsgraden ein kritischer Wert aus der Chi Quadrat Verteilungstabelle abgelesen werden, um den Chi Quadrat Wert an diesem Wert zu testen. Nur so kannst du feststellen, ob ein statistisch signifikanter Zusammenhang besteht.
Für Beispiel 1, den Zusammenhang zwischen Geschlecht und dem Spielen eines Instruments, hast du einen Chi Quadrat Wert von 12,81 berechnet. Das Signifikanzniveau legst du für eine Berechnung dieser Art ganz einfach auf 5% fest. In der Verteilungstabelle musst du daher in der Spalte mit dem Wert 0,950 nachschlagen. Die Freiheitsgrade musst du dagegen kurz berechnen. Hier spielt die Größe deiner Kreuztabelle eine Rolle, die im Beispiel 1 bekanntlich 2×2 war. Die Berechnung gestaltet sich dann dieser Formel folgend ganz einfach:
 = (Anzahl der Spalten – 1)
= (Anzahl der Spalten – 1)  (Anzahl der Zeilen – 1)
(Anzahl der Zeilen – 1)

Im Fall von Beispiel 1 kannst du jetzt also für ein Signifikanzniveau für 5% und einer Anzahl an Freiheitsgraden von  den relevanten kritischen Wert in der Chi Quadrat Verteilungstabelle nachschlagen.
den relevanten kritischen Wert in der Chi Quadrat Verteilungstabelle nachschlagen.
Für Beispiel 2 gilt zum Nachschlagen in der Tabelle ebenfalls das Signifikanzniveau von 5%. Die Anzahl der Freiheitsgrade liegt aber der Formel entsprechend bei  .
.
Chi Quadrat Tabelle
In der Verteilungstabelle liest du jetzt die richtigen kritischen Werte für die beiden Beispiele ab. Ohne diesen Schritt wäre der Chi Quadrat Test nicht vollständig durchgeführt und daher nicht aussagekräftig. Zum Ablesen siehst du hier nun den relevanten Ausschnitt aus der Chi Quadrat Verteilungstabelle .
| df \ Signifikanzniveau | 0,7 | 0,75 | 0,8 | 0,85 | 0,9 | 0,95 |
| 1 | 1,07 | 1,32 | 1,64 | 2,07 | 2,71 | 3,84 |
| 2 | 2,41 | 2,77 | 3,22 | 3,79 | 4,61 | 5,99 |
| 3 | 3,66 | 4,11 | 4,64 | 5,32 | 6,25 | 7,81 |
| 4 | 4,88 | 5,39 | 5,99 | 6,74 | 7,78 | 9,49 |
| 5 | 6,06 | 6,63 | 7,29 | 8,12 | 9,24 | 11,07 |
Anhand deiner Informationen über das Signifikanzniveau und die Anzahl der Freiheitsgrade kannst du für Beispiel 1 einen kritischen Wert von 3,84 ablesen. Der berechnete Chi Quadrat Wert liegt mit 12,81 deutlich darüber. Deshalb kannst du nach Durchführung des Chi Quadrat Test behaupten, dass zwischen den Variablen Geschlecht und Spielen eines Instruments ein statistisch signifikanter Zusammenhang besteht.
Für Beispiel 2 kannst du den kritischen Wert analog ebenfalls in der Tabelle nachschlagen und ermittelst dabei ein Ergebnis von 9,49. Auch hier liegt dein berechneter Chi Quadrat Wert mit 37,63 deutlich über dem kritischen Wert. Du kannst also durch den Chi Quadrat Test auch beim zweiten Beispiel einen Zusammenhang zwischen den betrachteten Variablen, nämlich Schulabschluss und Einkommen, herstellen.
Zusammenfassung Chi Quadrat Test
Zusammengefasst kann der Chi Quadrat Test also folgende Aussage treffen: besteht ein statistisch signifikanter Zusammenhang zwischen zwei Variablen oder sind die Variablen unabhängig zueinander?
Willst du allerdings detailliertere Behauptungen über den Zusammenhang deiner Variablen aufstellen, musst du weiterführende Berechnungen wie beispielsweise Phi , Cramers V oder den Kontingenzkoeffizienten von Pearson durchführen. Sie können nämlich Auskunft über die Richtung bzw. Stärke eines Zusammenhangs geben. Das kann der Chi Quadrat Test alleine stehend leider nicht leisten.



