Konfidenzintervall
Was ist ein Konfidenzintervall und ein Konfidenzniveau? Diese Frage und wie du das Konfidenzintervall berechnen kannst, die Zusammenhänge mit der Irrtumswahrscheinlichkeit und dem Standardfehler, zeigen wir dir hier.
Du willst dir das Thema lieber in kurzer Zeit anschaulich aneignen? In unserem Video erklären wir dir das Konfidenzintervall!
Konfidenzintervall einfach erklärt
Ganz einfach gesagt stellen Konfidenzintervalle einen statistisch berechneten Bereich dar, mit welchem man besser einschätzen kann, wo beispielsweise der wahre Mittelwert eines Datensatzes liegt. Das macht man, da in der Statistik berechnete Werte oft auf der Grundlage einer Stichprobe zustande kommen. Die Hypothesen und Prognosen sollen aber ja für ganze Personengruppen gelten.
Man kann beispielsweise die mittleren Ausgaben von 100 Studenten für Pizza heranziehen und um diesen Wert rechnerisch ein Konfidenzintervall aufspannen, in dem dann mit 95 prozentiger Sicherheit auch der Mittelwert der Ausgaben aller Studenten für Pizza liegt. Die schrittweise Berechnung für exakt dieses Beispiel wird nach Vorstellung der Definition im Verlauf des Beitrags noch verständlich erklärt werden.
Konfidenzintervall Definition
Unter dem Konfidenzintervall, abgekürzt auch KI genannt, ist ein statistisches Intervall zu verstehen, das die Lage eines wahren Parameters einer Grundgesamtheit mit einer gewissen Wahrscheinlichkeit lokalisieren soll.
Im Gegensatz zum geschätzten Parameter, der bekanntermaßen über Berechnungen mit den Daten einer Stichprobe zustande kommt, kann ein wahrer Parameter selten exakt bestimmt werden. Konfidenzintervalle bieten aber zumindest die Möglichkeit, ihn mit einer gewissen Erfolgswahrscheinlichkeit genauer verorten zu können.
Vertrauensintervall
Der Vollständigkeit halber ist noch anzumerken, dass das Konfidenzintervall in seltenen Fällen unter dem Namen Vertrauensintervall oder Vertrauensbereich vorkommt. Genauso kann man das Konfidenzniveau, auf das im Artikel gleich noch eingegangen wird, auch als Vertrauenswahrscheinlichkeit bezeichnen.
Konfidenzintervall Formel
Ein Konfidenzintervall besitzt immer zwei Endpunkte, die es vom Bereich der Irrtumswahrscheinlichkeit abgrenzen. Um das Intervall zu berechnen, benötigst du also die Werte für die sogenannte Ober- und Untergrenze. Die endgültigen Formeln zur Berechnung der Ober- und Untergrenze lauten so:
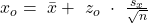
Hierbei stehen 
und 
respektive für die Untergrenze und die Obergrenze. 
bezeichnet den Mittelwert des Datensatzes, 
und 
sind die z-transformierten Intervallgrenzen. Zuletzt wird noch multipliziert mit dem Standardfehler, also dem Bruch aus der Standardabweichung 
und der Wurzel aus der Stichprobengröße 
.
Konfidenzintervall Beispiel
Man legt vor dem Start der Berechnung das angestrebte Konfidenzniveau fest, also mit welcher Wahrscheinlichkeit der wahre Mittelwert im bestimmten Konfidenzintervall liegen soll. Häufig richtet man sich hier an 95% aus, weshalb dieser Wert auch für das Beispiel gilt. Für dieses Beispiel ziehen wir uns Daten einer fiktiven Erhebung zum Pizzakonsum von Studenten heran. Hierbei betrachten wir die Ausgaben in € pro Monat pro Student anhand einer Stichprobengröße von 100 Studenten.
Das Ziel ist es, ein Konfidenzintervall um den geschätzten Mittelwert dieser Werte zu bestimmen, um so die Lage des wahren Mittelwerts der Grundgesamtheit einzugrenzen. Man bewegt sich mit diesem Beispiel auf der Normalverteilung, da ab einer Stichprobengröße von 50 von der t-Verteilung auf die Normalverteilung approximiert werden kann. Sind alle wichtigen Eckdaten und Voraussetzungen gesammelt und festgelegt, kann in die Berechnung gestartet werden.
Schritt 1: Berechnung des geschätzten Parameters:
Das Konfidenzintervall soll sich in diesem Beispiel um den folgenden geschätzten Parameter der Stichprobe aufspannen: den Mittelwert. Daher muss dieser in einem ersten Schritt berechnet werden. Aufgrund der hohen Stichprobengröße werden zur Vereinfachung gruppierte Daten verwendet.
| Anzahl Befragte | Ausgaben/Monat |
| 20 | 8€ |
| 30 | 32€ |
| 10 | 0€ |
| 30 | 48€ |
| 10 | 16€ |
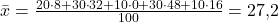
Für dieses Beispiel liegt der Mittelwert folglich bei 
.
Schritt 2: Transformation der Intervallgrenzen in normalverteilte Werte über die z-Verteilungstabelle
Durch das festgelegte Konfidenzniveau von 95% ergeben sich die folgenden Intervallgrenzen: die Untergrenze liegt bei 
% und die Obergrenze bei 
%. Diese Werte muss man nun standardisieren und hierfür in der z-Verteilungstabelle nachschlagen.
| 0,65 | 0,7 | 0,75 | 0,8 | 0,85 | 0,9 | 0,95 | 0,975 | 0,99 | 0,995 | |
| z-Wert | 0,385 | 0,524 | 0,674 | 0,842 | 1,036 | 1,282 | 1,645 | 1,960 | 2,326 | 2,576 |
Für die gesuchte Obergrenze lässt sich der z-Wert ganz einfach ablesen, denn er ist in Dezimalform als 0,975 in der Tabelle zu finden. Der Wert für die Untergrenze ist in der Tabelle nicht abgebildet, lässt sich aber folgendermaßen ermitteln:
Da die Normalverteilung symmetrisch und an der x-Achse gespiegelt ist, kann man einfach den Wert für die Obergrenze, also 
, ablesen und hierzu den Gegenwert, also 
, bilden. Somit sind also die z-transformierten Werte für die Ober- und Untergrenze des Konfidenzintervalls ermittelt: Sie liegen bei 
für die Untergrenze und 
für die Obergrenze. Mit einem Mittelwert , der Untergrenze 
, der Obergrenze 
und einer Stichprobengröße von 
sind alle benötigten Parameter für die Formel außer der Standardabweichung gegeben.
Standardfehler
Den Bruch 
aus der Standardabweichung und der Wurzel der Stichpobengröße n bezeichnest du auch als Standardfehler.
Normalverteilung
Die Angaben der Befragten wurden zur Veranschaulichung nochmal in einer Tabelle gruppiert.
| Anzahl Befragte | Ausgaben/Monat |
| 20 | 8€ |
| 30 | 32€ |
| 10 | 0€ |
| 30 | 48€ |
| 10 | 16€ |
Schritt 3: Berechnung von Varianz und Standardabweichung
Die Varianz lässt sich mit den Werten aus der Tabelle folgendermaßen berechnen:
Die Standardabweichung ist die Wurzel aus der Varianz. Also:
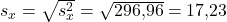
Jetzt kann man im letzten Schritt alle berechneten Werte in die Formeln übertragen.
Schritt 4: Alle Werte in die Formeln für Unter- und Obergrenze einsetzen
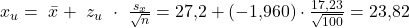
Die Grenzen des Kontingenzintervalls befinden sich also an den Punkten 23,82 und 30,58. Demnach befindet sich der wahre mit einer Wahrscheinlichkeit von 95% innerhalb dieses Bereichs. Die Schlussfolgerung für das Beispiel lautet: Mit einer Sicherheit von 95% liegt der wahre Mittelwert für die monatlichen Pizzaausgaben von Studenten zwischen 23,82€ und 30,58€.
95 Konfidenzintervall
Die Breite des Konfidenzintervalls, das heißt der Bereich, in dem der wahre Mittelwert der Grundgesamtheit erwartet wird, muss wie bereits erwähnt vor der Berechnung festgelegt werden. In den meisten Fällen ist es sinnvoll, mit einem Konfidenzintervall von 95% zu arbeiten. Bei dieser vorgegebenen Wahrscheinlichkeit handelt es sich um das sogenannte Konfidenzniveau. In seltenen Fällen kann man auch mit einem Konfidenzniveau von 99% arbeiten. Wenn z.B. die Sicherheit bzw. die Garantie, dass ein wahrer Wert im Konfidenzintervall angesiedelt ist, noch größer sein soll, dann kann man das Konfidenzniveau erhöhen und das Intervall somit ausdehnen. Die Breite des Konfidenzintervalls muss immer in Form einer Unter- und Obergrenze angegeben werden. Im konkreten Beispiel dieses Beitrags heißt das wie bereits erwähnt, dass sich das KI zwischen den Werten 23,83 und 30,58 aufspannt und sich in diesem Wertebereich zu 95% der wahre Mittelwert der Grundgesamtheit befindet.
Irrtumswahrscheinlichkeit
In Anlehnung an das 95 Konfidenzintervall lässt sich dann auch ganz einfach die Irrtumswahrscheinlichkeit ermitteln. Diese liegt im Falle eines 95% Konfidenzintervalls bei 5%. Bei einem Intervall mit einer Konfidenz von 99% läge die zugehörige Irrtumswahrscheinlichkeit demnach bei 1%. Folglich ist die Irrtumswahrscheinlichkeit die Differenz des Ganzen, also 100%, und der Größe des Konfidenzintervalls. Sie verteilt sich dann gleichmäßig auf beiden Seiten des Konfidenzintervalls.
Konfidenzintervall Übung
Wenn du dein Wissen gleich einsetzen möchtest, kannst du dich an unserem Übungsvideo probieren.
