Residuen
Du möchtest verstehen, was Residuen sind und warum sie möglichst klein sein sollen? Dann bist du in diesem Beitrag genau richtig!
Keine Lust zu lesen? Lehn dich zurück und erfahre in unserem Video ganz entspannt alles wichtige über Residuen.
Inhaltsübersicht
Residuen einfach erklärt
Residuen sind die Abweichung zwischen dem durch die Regressionsgleichung vorhergesagten Wert  und dem tatsächlich beobachteten Wert
und dem tatsächlich beobachteten Wert  in einer Regressionsanalyse
. Ein Residuum sagt folglich aus, wie weit du bei der Schätzung eines Kriteriumswerts daneben lagst. Angenommen du sagst etwa für eine Person ein Körpergewicht von 63 kg vorher, in Wahrheit wiegt die Person jedoch 66 kg, dann hättest du ein Residuum von
in einer Regressionsanalyse
. Ein Residuum sagt folglich aus, wie weit du bei der Schätzung eines Kriteriumswerts daneben lagst. Angenommen du sagst etwa für eine Person ein Körpergewicht von 63 kg vorher, in Wahrheit wiegt die Person jedoch 66 kg, dann hättest du ein Residuum von  . Residuen sollen stets möglichst klein sein, um eine exakte Vorhersage der Kriteriumswerte zu erhalten.
. Residuen sollen stets möglichst klein sein, um eine exakte Vorhersage der Kriteriumswerte zu erhalten.
Eine Residuum ist die Abweichung eines vorhergesagten Wertes vom tatsächlich beobachteten Wert. Der vorhergesagte Wert wurde dabei mithilfe eines mathematischen Modells ermittelt. Indem die Residuen minimiert werden, wird das Modell optimiert und es können genauere Vorhersagen getroffen werden.
Residuum Formel
Bei der Ermittlung der bestmöglichen Regressionsgleichung wird deshalb mathematisch versucht, die Residuen zu minimieren. Das geschieht mit Hilfe der Methode der kleinsten Quadrate. Allerdings werden die Residuen mit dieser Methode zwar minimiert, deine Vorhersage wird aber dennoch nicht perfekt sein. Wie groß die Residuen trotzdem noch werden, hängt dabei vor allem vom Zusammenhang zwischen den Prädiktoren und dem Kriterium
ab: Je stärker der Zusammenhang, desto genauer ist die Vorhersage und desto kleiner werden die Residuen.
Mathematisch notierst du ein Residuum so:

 – Residuum für den Prädiktorwert
– Residuum für den Prädiktorwert 
 – vorhergesagter Kriteriumswert
– vorhergesagter Kriteriumswert  – tatsächlich beobachteter Kriteriumswert
– tatsächlich beobachteter Kriteriumswert
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Grafische Veranschaulichung
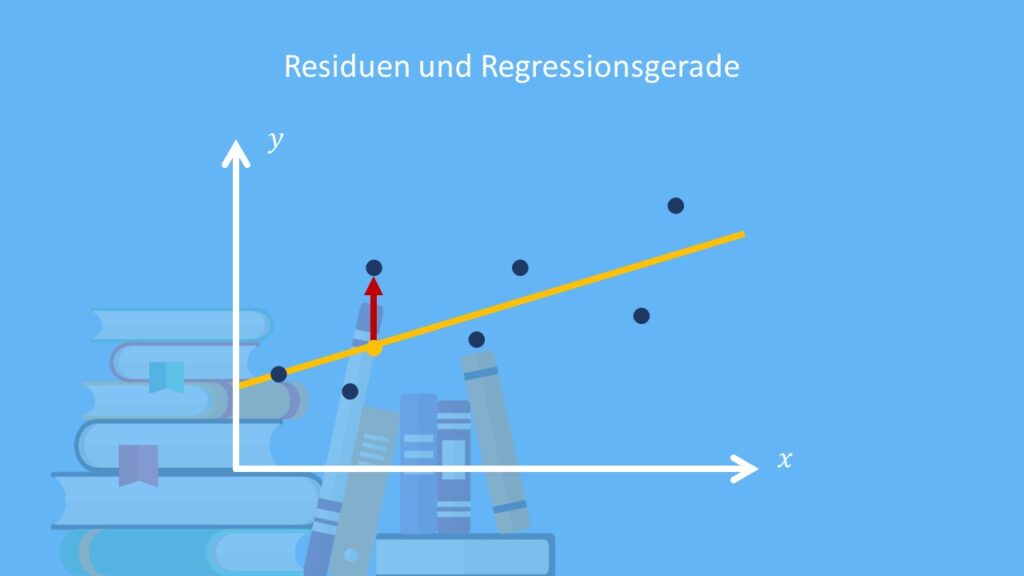
Mit Hilfe eines Streudiagramms und der Regressionsgeraden kannst du dir Residuen bildlich veranschaulichen:
Ein Residuum ist der senkrechte Abstand zwischen der Regressionsgeraden und einem beobachteten Messwert. Es zeigt dir also für einen bestimmten Prädiktorwert die Differenz zwischen dem vorhergesagten Wert  (Punkt auf der Regressionsgerade) und dem tatsächlich beobachteten Wert
(Punkt auf der Regressionsgerade) und dem tatsächlich beobachteten Wert  (Punkt aus der Punktwolke). Residuen können dabei positiv oder negativ sein – abhängig davon, ob der beobachtete Wert über oder unter der Regressionsgerade liegt.
(Punkt aus der Punktwolke). Residuen können dabei positiv oder negativ sein – abhängig davon, ob der beobachtete Wert über oder unter der Regressionsgerade liegt.
Eigenschaften
Der Erwartungswert von Residuen ist stets 0. Das liegt daran, dass die Regressionsgerade so in die Punktwolke der Messwerte hineingelegt wird, dass sich die Residuen symmetrisch um die Regressionsgerade verteilen. Dadurch gleichen sich positive und negative Residuen zu 0 aus.
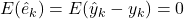
Für Residuen müssen bei der linearen Regression zudem einige weitere wichtige Annahmen gelten. Etwa ist es wichtig, dass die Residuen normalverteilt und unkorreliert sind. Eine ebenfalls wichtige Annahme ist die Homoskedastiziät . Das bedeutet, dass die Varianz der Residuen immer gleich ist und nicht mit dem vorhergesagten Wert zusammenhängt.
Varianzzerlegung
Residuen bilden zudem die Grundlage zur Varianzzerlegung bei der Regressionsanalyse. Vielleicht hast du bereits davon gehört, dass sich die Varianz der abhängigen Variable bei der Regressionsanalyse in mehrere Komponenten aufteilen lässt. Diese Komponenten sind zum einen ein Teil der Varianz, der mit Hilfe der Prädiktoren erklärt werden kann und ein Teil, der nicht aufgeklärt werden kann.
Mit Hilfe der Residuen kannst du den Teil der Varianz schätzen, der nicht mit den Prädiktoren aufgeklärt werden konnte:

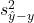 – Residualvarianz
– Residualvarianz  – vorhergesagter Kriteriumswert
– vorhergesagter Kriteriumswert  – beobachteter Kriteriumswert
– beobachteter Kriteriumswert
Je nach dem, wie groß der Anteil dieser sogenannten Residualvarianz an der gesamten Varianz deiner abhängigen Variable ist, konntest du das Kriterium mehr oder weniger gut vorhersagen.
Wenn du noch mehr über die Varianzerlegung erfahren möchtest, dann sieh dir unseren Beitrag zum Bestimmtheitsmaß an.