Multiple Regression
Du fragst dich, was die multiple Regression ist und wie sie sich von der einfachen linearen Regression unterscheidet? In diesem Beitrag erfährst du alles, was du über die Bedeutung, Berechnung und die Interpretation der multiplen linearen Regression wissen musst.
Keine Lust zu lesen? Kein Problem, dann schau dir doch unser Video an und werde im Handumdrehen zum Experten im Bereich der multiplen Regression!
Inhaltsübersicht
Multiple Regression einfach erklärt
Mit der multiplen linearen Regression (auch kurz einfach: multiple Regression) kannst du die Werte einer abhängigen Variablen mit Hilfe mehrerer unabhängiger Variablen vorhersagen. Während du bei der einfachen linearen Regression nur einen Prädiktor betrachtest, verwendest du bei der multiplen linearen Regression also mehrere Prädiktoren, um das Kriterium zu schätzen.
Das hat den Vorteil, dass du mehrere Einflussfaktoren gleichzeitig in deiner Vorhersage berücksichtigen kannst. Dadurch wird deine Vorhersage genauer und du kannst mehr Varianz des Kriteriums aufklären. Hierbei gilt genau wie bei nur einem Prädiktor: Je stärker der Zusammenhang der Prädiktorvariablen mit dem Kriterium, desto exakter lassen sich die die Werte des Kriteriums vorhersagen.
Anwendungsbereiche der multiplen Regression
Neben der Vorhersage von neuen Kriteriumswerten kannst du mit der multiplen Regression untersuchen, wie verschiedene Variablen miteinander zusammenhängen. Das ist zum Beispiel wichtig, wenn du Hypothesen darüber aufstellst, welche Variablen einen besonders starken Einfluss auf das Kriterium haben und wie sich dieser Einfluss verändert, wenn du noch weitere Prädiktoren in die Regression mit aufnimmst.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Multiple Regression Beispiel
Sehen wir uns die multiple lineare Regression an einem Beispiel an.
Stell dir vor, du veranstaltest ein Festival und möchtest schätzen, mit wie vielen Gästen du ungefähr rechnen kannst. Dafür betrachtest du, welche Faktoren in den letzten Jahren besonders großen Einfluss darauf hatten, wie viele Personen das Festival besucht haben.
Gemäß deiner Recherche sind folgende drei Variablen besonders relevant für das Gästeaufkommen:
- Der Ticketpreis
- Die Außentemperatur am Tag des Festivals
- Das Beliebtheitsranking der auftretenden Bands (Skala 1-100)
Mit Hilfe dieser drei Prädiktoren möchtest du nun dein Kriterium „Gästezahl auf dem Festival“ vorhersagen.
Zum Vergleich: Bei der einfachen linearen Regression hättest du nur einen der drei Prädiktoren betrachtet. Sowohl bei der einfachen als auch bei der multiplen linearen Regression verwendest du jedoch immer nur ein einziges Kriterium.
Multiple Regression: Regressionsgleichung
Um nun die erwartete Gästezahl vorhersagen zu können, musst du die Regressionsgleichung aufstellen. Die Regressionsgleichung kennst du bestimmt schon von der einfachen linearen Regression. In sie kannst du beliebige Werte auf den Prädiktorvariablen einsetzen und erhältst eine Schätzung für die Kriteriumsvariable. Das bedeutet, du setzt einen Ticketpreis, eine Außentemperatur und ein Beliebtheitsrating in die Gleichung ein und erhältst, wie viele Gäste unter diesen Umständen voraussichtlich zu erwarten sind.
Im Allgemeinen sieht die Regressionsgleichung bei der multiplen linearen Regression für eine beliebige Anzahl  an Prädiktoren so aus:
an Prädiktoren so aus:

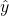 – Wert auf der Kriteriumsvariable, der vorhergesagt werden soll
– Wert auf der Kriteriumsvariable, der vorhergesagt werden soll  – Regressionsgewicht des ersten Prädiktors
– Regressionsgewicht des ersten Prädiktors  – Messwert auf dem ersten Prädiktor
– Messwert auf dem ersten Prädiktor  – Regressionsgewicht eines beliebigen Prädiktors
– Regressionsgewicht eines beliebigen Prädiktors 
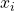 – Messwert auf dem beliebigen Prädiktor
– Messwert auf dem beliebigen Prädiktor 
 – Regressionsgewicht des letzten Prädiktors
– Regressionsgewicht des letzten Prädiktors 
 – Messwert auf dem letzten Prädiktor
– Messwert auf dem letzten Prädiktor 
 – Regressionskonstante
– Regressionskonstante
Im Fall von unserem Beispiel mit 3 Prädiktoren würde die Regressionsgleichung also folgendermaßen lauten:

Die Regressionskonstante  wird zu Beginn einmal berechnet und bleibt dann für die komplette Regression gleich. Die Regressionsgewichte
wird zu Beginn einmal berechnet und bleibt dann für die komplette Regression gleich. Die Regressionsgewichte  sind ebenfalls feste Werte, sie unterscheiden sich aber zwischen den verschiedenen Prädiktoren. Die Messwerte
sind ebenfalls feste Werte, sie unterscheiden sich aber zwischen den verschiedenen Prädiktoren. Die Messwerte  sind hingegen variabel und werden immer wieder neu eingesetzt, je nach dem für welche Prädiktorwerte du das Kriterium vorhersagen möchtest.
sind hingegen variabel und werden immer wieder neu eingesetzt, je nach dem für welche Prädiktorwerte du das Kriterium vorhersagen möchtest.
Regressionsgleichung aufstellen
Bevor du also Werte mit deiner Regressionsgleichung vorhersagen kannst, musst du die Regressionskonstante  und die Regressionsgewichte
und die Regressionsgewichte  bestimmen.
bestimmen.
Für die Ermittlung der Regressionskoeffizienten der multiplen Regression musst du zunächst ein Gleichungsystem aus den standardisierten Regressionsgewichten  , den Interkorrelationen zwischen den verschiedenen Prädiktoren
, den Interkorrelationen zwischen den verschiedenen Prädiktoren 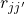 sowie den Korrelationen zwischen den Prädiktoren und dem Kriterium
sowie den Korrelationen zwischen den Prädiktoren und dem Kriterium  aufstellen. Da die Interkorrelationen sowie die Prädiktor-Kriteriums-Korrelationen bekannt sind, kannst du durch Umstellen und Einsetzen das Gleichungssystem lösen. In einem nächsten Schritt kannst du anschließend die unstandardisierten Regressionsgewichte
aufstellen. Da die Interkorrelationen sowie die Prädiktor-Kriteriums-Korrelationen bekannt sind, kannst du durch Umstellen und Einsetzen das Gleichungssystem lösen. In einem nächsten Schritt kannst du anschließend die unstandardisierten Regressionsgewichte  und die Regressionskonstante
und die Regressionskonstante  bestimmen.
bestimmen.
Da das Aufstellen der Regressionsgleichung der multiplen Regression sehr mühsam ist und selten per Hand durchgeführt wird, verzichten wir an dieser Stelle auf eine ausführliche Beschreibung des Vorgehens. Stattdessen verwendet man in der Praxis meist einfach ein Statistikprogramm, dass dir die fertige Regressionsgleichung automatisch ausspuckt.
Regressionsgleichung: Kriteriumswerte schätzen
Im Falle deines Festivals könnte die Regressionsgleichung etwa so aussehen:
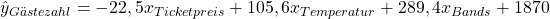
Angenommen du möchtest also vorhersagen, wie viele Besucher und Besucherinnen du auf dem Festival erwarten kannst, wenn die Tickets 175 € kosten, eine Temperatur von 28 Grad gemessen wird und die Bands ein Beliebtheitsrating von 83 (aus 100) absahnen konnten. Dafür setzt du also in die Regressionsgleichung ein und rechnest aus:

Unter diesen Bedingungen kannst du also mit etwa 24909,5 Besuchern und Besucherinnen auf dem Festival rechnen.
Regressionskoeffizienten: Inhaltliche Bedeutung
Sehen wir uns nun noch an, wie du die Regressionskoeffizienten inhaltlich interpretieren kannst.
Zunächst die Regressionskonstante  : Die Regressionskonstante
: Die Regressionskonstante  sagt aus, welchen Wert das Kriterium
sagt aus, welchen Wert das Kriterium  annehmen würde, wenn alle Prädiktoren 0 sind. In Unserem Beispiel gibt die Regressionskonstante also an, wie viele Personen das Festival besuchen würden, wenn es 0€ kosten würde, die Außentemperatur 0 Grad betrüge und die Bands maximal unbeliebt wären und einen Beliebtheitsscore von 0 hätten. Ob die Interpretation von
annehmen würde, wenn alle Prädiktoren 0 sind. In Unserem Beispiel gibt die Regressionskonstante also an, wie viele Personen das Festival besuchen würden, wenn es 0€ kosten würde, die Außentemperatur 0 Grad betrüge und die Bands maximal unbeliebt wären und einen Beliebtheitsscore von 0 hätten. Ob die Interpretation von  überhaupt inhaltlich sinnvoll ist, hängt dabei immer von den betrachteten Variablen ab.
überhaupt inhaltlich sinnvoll ist, hängt dabei immer von den betrachteten Variablen ab.
Die Regressionskoeffizienten  geben an, um wie viele Einheiten das Kriterium ansteigt oder sinkt, wenn die zugehörige Prädiktorvariable um 1 ansteigt. Steigt also etwa das Beliebtheitsrating der Bands um 1 an, kommen schätzungsweise 289,4 mehr Personen zum Festival. Steigt hingegen der Preis um 1€, dann kommen 22,5 Personen weniger.
geben an, um wie viele Einheiten das Kriterium ansteigt oder sinkt, wenn die zugehörige Prädiktorvariable um 1 ansteigt. Steigt also etwa das Beliebtheitsrating der Bands um 1 an, kommen schätzungsweise 289,4 mehr Personen zum Festival. Steigt hingegen der Preis um 1€, dann kommen 22,5 Personen weniger.
Es ist wichtig zu beachten, dass der Regressionskoeffizient  eines Prädiktors immer auch davon abhängt, welche anderen Prädiktoren du noch in deiner multiplen Regression betrachtest. Häufig hängen die Prädiktoren nämlich auch untereinander zusammen und klären teilweise die gleichen Varianzanteile des Kriteriums auf. Um diese Varianzanteile nicht doppelt zu berücksichtigen, werden die
eines Prädiktors immer auch davon abhängt, welche anderen Prädiktoren du noch in deiner multiplen Regression betrachtest. Häufig hängen die Prädiktoren nämlich auch untereinander zusammen und klären teilweise die gleichen Varianzanteile des Kriteriums auf. Um diese Varianzanteile nicht doppelt zu berücksichtigen, werden die  -Gewichte so berechnet, dass der Einfluss zwischen den Prädiktoren aufgeteilt wird. Würdest du nun einen der Prädiktoren entfernen, ist das nicht mehr nötig. Folglich würde sich der Regressionskoeffizient
-Gewichte so berechnet, dass der Einfluss zwischen den Prädiktoren aufgeteilt wird. Würdest du nun einen der Prädiktoren entfernen, ist das nicht mehr nötig. Folglich würde sich der Regressionskoeffizient  dieses Prädiktors verändern. Entfernst du also etwa den Prädiktor „Beliebtheit der Bands“, könnte der Einfluss des „Ticketpreises“ steigen, da sich die beiden Prädiktoren zuvor die gleichen Varianzanteile des Kriteriums „geteilt“ haben.
dieses Prädiktors verändern. Entfernst du also etwa den Prädiktor „Beliebtheit der Bands“, könnte der Einfluss des „Ticketpreises“ steigen, da sich die beiden Prädiktoren zuvor die gleichen Varianzanteile des Kriteriums „geteilt“ haben.
Multiple Regression: Interpretation und Anwendung
Neben der Vorhersage neuer Kriteriumswerte kannst du die multiple Regression auch verwenden, um zu untersuchen, wie verschiedene Variablen miteinander zusammenhängen. Dabei kannst du dir etwa ansehen, in wie weit der Einfluss von bestimmten Variablen überhaupt noch relevant ist, wenn du noch weitere Variablen in dein Modell mit aufnimmst oder welche Varianzanteile ein Prädiktor ganz alleine aufklärt.
Berechnest du die Regression mit einem Statistikprogramm, werden dir direkt einige interessante Kennzahlen mit ausgegeben. Das Bestimmtheitsmaß  sagt dir etwa, welchen Anteil der Varianz des Kriteriums du mit Hilfe all deiner Prädiktoren insgesamt erklären kannst. In anderen Worten gibt es also an, wie exakt du das Kriterium mit Hilfe der Prädiktoren vorhersagen kannst. Daneben kannst du dir im Output deines Statistikprogramms auch ansehen, ob es Varianzanteile gibt, die nur von einem einzigen Prädiktoren aufgeklärt werden. Dafür betrachtest du die Semipartialkorrelationen der einzelnen Prädiktoren. Praktischerweise liefert das Statistikprogramm auch direkt Informationen darüber, ob die verschiedenen Statistiken signifikant sind. Das ist besonders wichtig, wenn du die Aussagen aus deiner Untersuchung auf eine Grundgesamtheit übertragen möchtest.
sagt dir etwa, welchen Anteil der Varianz des Kriteriums du mit Hilfe all deiner Prädiktoren insgesamt erklären kannst. In anderen Worten gibt es also an, wie exakt du das Kriterium mit Hilfe der Prädiktoren vorhersagen kannst. Daneben kannst du dir im Output deines Statistikprogramms auch ansehen, ob es Varianzanteile gibt, die nur von einem einzigen Prädiktoren aufgeklärt werden. Dafür betrachtest du die Semipartialkorrelationen der einzelnen Prädiktoren. Praktischerweise liefert das Statistikprogramm auch direkt Informationen darüber, ob die verschiedenen Statistiken signifikant sind. Das ist besonders wichtig, wenn du die Aussagen aus deiner Untersuchung auf eine Grundgesamtheit übertragen möchtest.
Noch mehr Regressionsanalyse?
Du möchtest noch mehr über verschiedene Arten der Regressionsanalyse, ihre Kennzahlen und Eigenschaften erfahren? Kein Problem, schau doch einfach mal hier vorbei!