Lineare Regression
In diesem Artikel erklären wir dir worum es bei der linearen Regression geht und wie du bei der Berechnung vorgehen musst. Dafür sehen wir uns ein Beispiel an und erläutern daran die Regressionsgleichung und die Regressionsgerade.
Du möchtest die lineare Regression noch schneller verstehen? Dann sieh dir unser Video an und erfahre dort alles, was du über das Thema wissen musst.
Inhaltsübersicht
Lineare Regression einfach erklärt
Bei der linearen Regression versuchst du die Werte einer Variablen mit Hilfe einer oder mehrerer anderer Variablen vorherzusagen. Die Variable, die vorhergesagt werden soll, wird Kriterium oder abhängige Variable genannt. Die Variablen, die zur Vorhersage genutzt werden, werden als Prädiktoren oder als unabhängige Variablen bezeichnet.
Für die Vorhersage des Kriteriums betrachtest du den Zusammenhang zwischen den Prädiktoren und dem Kriterium. Je enger der Zusammenhang, desto besser kannst du das Kriterium vorhersagen. Wie der Name schon vermuten lässt, werden bei der linearen Regression jedoch nur lineare Zusammenhänge betrachtet.
Regressionsgleichung und Regressionsgerade
Um mit Hilfe der Prädiktoren das Kriterium vorherzusagen, musst du eine sogenannte Regressionsgleichung aufstellen. In diese Gleichung kannst du beliebige Werte der Prädiktorvariablen einsetzen und erhältst eine Schätzung für das Kriterium. Mittels der Regressionsgeraden kannst du die lineare Regression auch bildlich darstellen. An der Regressionsgeraden kannst du ungefähr ablesen, welche Werte des Kriteriums für welche Prädiktorwerte vorhergesagt werden. Zudem kannst du mit ihrer Hilfe einschätzen, wie hoch etwa die Korrelation zwischen Prädiktor und Kriterium ist.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lineare Regression Beispiel
Sehen wir uns die lineare Regression an einem Beispiel an.
Stell dir vor du bist Bademeister bzw. Bademeisterin in einem Freibad. Aus organisatorischen Gründen möchtest du gerne wissen, wie viele Personen du am nächsten Tag im Schwimmbad erwarten kannst. In der vergangenen Saison hast du dir einige Notizen gemacht, wie viele Besucher und Besucherinnen bei welcher Temperatur schwimmen waren.
Temperatur in °C 
|
28 | 23 | 32 | 35 | 29 | 30 | 27 | 34 | 32 |
Gästezahl 
|
400 | 60 | 630 | 560 | 290 | 620 | 440 | 610 | 250 |
Laut dem Wetterbericht soll es am nächsten Tag 33 Grad warm werden. Beim Blick in deine Aufzeichnungen musst du jedoch feststellen, dass du für diese Gradzahl noch keine Eintragung gemacht hast. Du möchtest aber trotzdem gerne wissen, wie viele Gäste du am nächsten Tag erwarten kannst. Folglich beschließt du die erwartete Besucherzahl zu schätzen. Bei dieser Schätzung hilft dir die lineare Regression.
Mit der linearen Regression kannst du für jede beliebige Temperatur schätzen, wie viele Leute ins Freibad kommen werden. Dafür erstellst du eine Regressionsgleichung. In diese Gleichung kannst du einen Temperaturwert deiner Wahl einsetzen und erhältst als Ergebnis die erwartete Besucherzahl.
Regressionsgleichung
Wie kommst du also an diese Regressionsgleichung? Die allgemeine Form der Regressionsgleichung sieht bei der einfachen linearen Regression so aus:

 – Vorhergesagter Wert auf dem Kriterium
– Vorhergesagter Wert auf dem Kriterium  für den k-ten Messwert
für den k-ten Messwert
 – k-ter Messwert auf dem Prädiktor
– k-ter Messwert auf dem Prädiktor 
 – Regressionsgewicht, Steigung der Regressionsgeraden
– Regressionsgewicht, Steigung der Regressionsgeraden
 – y-Achsenabschnitt der Regressionsgeraden
– y-Achsenabschnitt der Regressionsgeraden
 ist das Kriterium, also die Variable die du vorhersagen möchtest.
ist das Kriterium, also die Variable die du vorhersagen möchtest.  ist die Variable. die du für die Vorhersage nutzt, also der Prädiktor.
ist die Variable. die du für die Vorhersage nutzt, also der Prädiktor.  steht dafür, um wie viele Einheiten deine abhängige Variable ansteigt, wenn deine unabhängige Variable um 1 steigt.
steht dafür, um wie viele Einheiten deine abhängige Variable ansteigt, wenn deine unabhängige Variable um 1 steigt.  ist der Wert, den die abhängige Variable annimmt, wenn der Prädiktor 0 ist. Ob eine Interpretation von
ist der Wert, den die abhängige Variable annimmt, wenn der Prädiktor 0 ist. Ob eine Interpretation von  inhaltlich Sinn ergibt, hängt von den betrachteten Variablen ab. Möchtest du etwa das Gewicht einer Person mit Hilfe ihrer Körpergröße schätzen, ist es wenig einleuchtend, das Gewicht einer Person mit der Körpergröße von 0 cm zu interpretieren.
inhaltlich Sinn ergibt, hängt von den betrachteten Variablen ab. Möchtest du etwa das Gewicht einer Person mit Hilfe ihrer Körpergröße schätzen, ist es wenig einleuchtend, das Gewicht einer Person mit der Körpergröße von 0 cm zu interpretieren.
Regressionsgleichung erstellen
Wenn du die Regressionsgleichung in der Praxis selbst erstellen möchtest, dann berechnest du zunächst die Mittelwerte
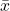 und
und  sowie die Standardabweichungen
sowie die Standardabweichungen
 und
und  deiner unabhängigen und deiner abhängigen Variablen. In unserem Beispiel ist die unabhängige Variable
deiner unabhängigen und deiner abhängigen Variablen. In unserem Beispiel ist die unabhängige Variable  die Temperatur und die abhängige Variable
die Temperatur und die abhängige Variable  die Besucherzahl.
die Besucherzahl.




Anschließend berechnest du die Kovarianz
 und die Korrelation
und die Korrelation
 .
.


Mit Hilfe dieser Werte kannst du nun die Regressionsgleichung bestimmen.
 berechnest du so:
berechnest du so:

Und auf  kommst du mit folgender Formel:
kommst du mit folgender Formel:

Damit hast du deine Regressionsgleichung erstellt. Sie lautet folgendermaßen:

In diese Formel kannst du nun die Temperatur einsetzen, für die du die Gästezahl vorhersagen möchtest. Setzen wir also die Temperatur des nächsten Tags, also 33 Grad, für den Prädiktor  ein.
ein.

Als Ergebnis erhältst du eine Schätzung für die abhängige Variable „Gästezahl“. Basierend auf deinen Aufzeichnungen aus dem letzten Jahr sind am morgigen Tag also 540,5 Besucher und Besucherinnen zu erwarten.
Natürlich kann die wahre Zahl der Gäste von deiner vorhergesagten Besucherzahl abweichen. Es ist ja schließlich auch nur eine Schätzung. Diese Abweichung zwischen dem wahren und dem vorhergesagten Wert wird als Residuum bezeichnet.
Regressionsgerade
Wenn du dir die Regressionsgleichung der einfachen linearen Regression ansiehst, erkennst du, dass sie den Aufbau einer linearen Funktion hat.

Die Gerade dieser Funktion kannst du in ein Koordinatensystem eintragen. Sie wird als Regressionsgerade bezeichnet. An der Regressionsgerade kannst du optisch abschätzen, wie stark der Zusammenhang zwischen dem Prädiktor und dem Kriterium ist: Eine ansteigende Gerade steht hierbei für einen positiven Zusammenhang, eine abfallende für einen negativen.
Die kleinen Punkte in dem Koordinatensystem sind die einzelnen Messwerte, die du in deiner Untersuchung beobachtet hast. In unserem Beispiel sind das deine Aufzeichnungen vom letzten Jahr, also bei welcher Temperatur wie viele Gäste im Schwimmbad waren. In diese Punktwolke soll die Regressionsgerade so hineingelegt werden, dass sie möglichst nah an allen Punkten liegt und so die Daten möglichst gut abbildet.
Warum eigentlich „lineare“ Regression?
An der Regressionsgerade kannst du zudem erkennen, weshalb die lineare Regression nur für lineare Zusammenhänge geeignet ist. Angenommen zwei Variablen stünden nicht in einem linearen, sondern in einem quadratischen Zusammenhang.
Wie du siehst, wäre es sehr schwierig hier eine Regressionsgerade einzuzeichnen, die möglichst nah an allen Punkten liegt. Und auch wenn du die Produkt-Moment-Korrelation berechnen würdest, würde das Ergebnis voraussichtlich nahe bei 0 liegen. Das bedeutet jedoch nicht, dass kein Zusammenhang zwischen den Variablen besteht. Stattdessen ist der Zusammenhang einfach nur nicht linear, weshalb du ihn mit der linearen Regression nicht gut beschreiben kannst. Anders ausgedrückt kannst du Werte des Kriteriums mit der linearen Regression also nur erfolgreich vorhersagen, wenn der Zusammenhang zwischen dem Prädiktor und dem Kriterium auch tatsächlich linear ist.
Aus dieser Beobachtung ergibt sich eine weitere Anwendung der linearen Regression. Neben der Vorhersage von neuen Werten kannst du mit der linearen Regression auch überprüfen, ob Variablen wirklich einen linearen Zusammenhang haben. Kannst du mit der linearen Regression Werte verlässlich schätzen, dann spricht das dafür, dass die Variablen in einem linearen Verhältnis zueinander stehen.
Einfache lineare Regression und multiple lineare Regression
In diesem Beitrag haben wir uns die lineare Regression anhand der einfachen linearen Regression angesehen. Neben der einfachen linearen Regression gibt es jedoch auch noch die multiple lineare Regression. Der Unterschied zwischen den beiden Regressionsarten ist die Anzahl der Prädiktoren. Während bei der einfachen linearen Regression nur ein einziger Prädiktor betrachtet wird, werden bei der multiplen linearen Regression mehrere Prädiktoren verwendet, um das Kriterium noch genauer vorhersagen zu können. Wenn du noch mehr zur multiplen linearen Regression erfahren möchtest, dann sieh dir gerne unseren separaten Beitrag dazu an.

