Regressionskoeffizient
Du fragst dich, wie du den Regressionskoeffizient interpretieren und berechnen kannst? In diesem Beitrag erfährst du alles, was du wissen musst! Du lernst lieber audiovisuell? Kein Problem, dann ist unser Video der perfekte Lernhelfer für dich!
Inhaltsübersicht
Regressionskoeffizient einfach erklärt
Regressionskoeffizienten bilden in der Regressionsanalyse
den Einfluss verschiedener Prädiktorvariablen
in der Regressionsgleichung ab. Die Regressionsgewichte  geben dabei an, um wie viele Einheiten der Wert der Kriteriumsvariable
steigt oder sinkt, wenn die Prädiktorvariable um 1 größer wird. Die Regressionskonstante
geben dabei an, um wie viele Einheiten der Wert der Kriteriumsvariable
steigt oder sinkt, wenn die Prädiktorvariable um 1 größer wird. Die Regressionskonstante  sagt hingegen aus, welchen Wert die Kriteriumsvariable annimmt, wenn alle Prädiktoren den Wert 0 haben. Ob die Interpretation von
sagt hingegen aus, welchen Wert die Kriteriumsvariable annimmt, wenn alle Prädiktoren den Wert 0 haben. Ob die Interpretation von  inhaltlich sinnvoll ist, hängt dabei aber immer von den betrachteten Variablen ab.
inhaltlich sinnvoll ist, hängt dabei aber immer von den betrachteten Variablen ab.
Standardisierte und unstandardisierte Regressionsgewichte
Bei den Regressionsgewichten  unterscheidet man zwischen den standardisierten und den unstandardisierten Regressionsgewichten. Die standardisierten Koeffizienten werden dabei mit
unterscheidet man zwischen den standardisierten und den unstandardisierten Regressionsgewichten. Die standardisierten Koeffizienten werden dabei mit  („beta“), die unstandardisierten mit
(„beta“), die unstandardisierten mit  bezeichnet. Die Regressionskonstante
bezeichnet. Die Regressionskonstante  , fällt bei der standardisierten Regressionsgleichung komplett weg. Abhängig davon, ob du die standardisierten oder unstandardisierten Regressionskoeffizienten betrachtest, ändert sich ihre Interpretation ein wenig.
, fällt bei der standardisierten Regressionsgleichung komplett weg. Abhängig davon, ob du die standardisierten oder unstandardisierten Regressionskoeffizienten betrachtest, ändert sich ihre Interpretation ein wenig.
Um die Regressionsgleichung aufstellen zu können, musst du die Regressionskoeffizienten zunächst berechnen. Wie das funktioniert, erfährst du weiter unten in diesem Beitrag! In die fertige Regressionsgleichung kannst du dann Prädiktorwerte deiner Wahl einsetzen und erhältst eine Schätzung für den Wert der Kriteriumsvariable.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Regressionskoeffizient: Interpretation
Allgemein sieht die Regressionsgleichung der einfachen linearen Regression mit unstandardisierten Koeffizienten so aus:

Der Regressionskoeffizient  gibt dabei an, um wie viele Einheiten der Wert des Kriteriums ansteigt oder abfällt, wenn der Prädiktor um 1 größer wird. Die Regressionskonstante
gibt dabei an, um wie viele Einheiten der Wert des Kriteriums ansteigt oder abfällt, wenn der Prädiktor um 1 größer wird. Die Regressionskonstante  sagt hingegen aus, welchen Wert das Kriterium annimmt, wenn der Prädiktor gleich 0 ist.
sagt hingegen aus, welchen Wert das Kriterium annimmt, wenn der Prädiktor gleich 0 ist.
Damit du dir das ein bisschen besser vorstellen kannst, sehen wir uns ein Beispiel an: Stell‘ dir vor, du möchtest vorhersagen, wie viele Personen ein Festival besuchen werden. Als Prädiktor verwendest du dafür den Preis des Festivaltickets. Du rechnest also eine Regressionsanalyse und erhältst folgende Regressionsgleichung.


Doch wie kannst du  und
und  in diesem Fall nun interpretieren?
in diesem Fall nun interpretieren?
Das Regressionsgewicht  gibt an, um wie viel der Wert des Kriteriums ansteigt oder abfällt, wenn der Wert des Prädiktors um 1 ansteigt. In unserem Fall sagt es also aus, wie viele Gäste mehr oder weniger kommen, wenn der Ticketpreis um 1€ ansteigt. Du siehst, dass der Regressionskoeffizient hier
gibt an, um wie viel der Wert des Kriteriums ansteigt oder abfällt, wenn der Wert des Prädiktors um 1 ansteigt. In unserem Fall sagt es also aus, wie viele Gäste mehr oder weniger kommen, wenn der Ticketpreis um 1€ ansteigt. Du siehst, dass der Regressionskoeffizient hier  beträgt. Folglich kommen für jeden Euro, den das Ticket teurer wird, schätzungsweise 60 Leute weniger zum Festival.
beträgt. Folglich kommen für jeden Euro, den das Ticket teurer wird, schätzungsweise 60 Leute weniger zum Festival.
Die Regressionskonstante  gibt an, welchen Wert das Kriterium annimmt, wenn der Prädiktor 0 ist. In unserem Beispiel sagt sie also aus, wie viele Personen das Festival schätzungsweise besuchen würden, wenn der Eintritt 0€, also kostenlos, wäre. In diesem Fall könntest du mit ungefähr 50172,01 Besuchern und Besucherinnen rechnen.
gibt an, welchen Wert das Kriterium annimmt, wenn der Prädiktor 0 ist. In unserem Beispiel sagt sie also aus, wie viele Personen das Festival schätzungsweise besuchen würden, wenn der Eintritt 0€, also kostenlos, wäre. In diesem Fall könntest du mit ungefähr 50172,01 Besuchern und Besucherinnen rechnen.
Standardisierte Regressionskoeffizienten
Neben der oben vorgestellten, unstandardisierten Regressionsgleichung kannst du auch eine standardisierte Regressionsgleichung erstellen. Für die standardisierte Regressionsgleichung benötigst du entweder z-standardisierte Messwerte oder du formst die unstandardisierte Regressionsgleichung um. Durch die Standardisierung werden die Skalierungen der einzelnen Prädiktoren herausgerechnet. In der Folge kannst du die Regressionskoeffizienten verschiedener Prädiktoren miteinander vergleichen und besser einschätzen, wie groß ihr Einfluss auf das Kriterium ist. Das geht bei unstandardisierten Regressionskoeffizienten nicht so einfach, da deren Höhe immer auch vom Mittelwert und der Streuung des jeweiligen Prädiktors abhängt.
Die standardisierte Regressionsgleichung sieht allgemein so aus:

Du siehst, dass die Regressionskonstante a durch die Standardisierung ganz weggefallen ist. Die standardisierte Regressionsgerade verläuft in der Folge auch stets durch den Ursprung des Koordinatensystems. Zudem werden die Regressionsgewichte nun nicht mehr mit b, sondern mit  („beta“ )bezeichnet. Hast du nur einen Prädiktor, dann entspricht das Regressionsgewicht
(„beta“ )bezeichnet. Hast du nur einen Prädiktor, dann entspricht das Regressionsgewicht  einfach der Korrelation zwischen dem Prädiktor und dem Kriterium.
einfach der Korrelation zwischen dem Prädiktor und dem Kriterium.
Du kannst standardisierte Regressionsgewichte folgendermaßen interpretieren:
Steigt dein Prädiktor um eine standardisierte Einheit an, dann steigt das Kriterium um beta standardisierte Einheiten an.
Regressionskoeffizient berechnen
Im Falle einer einfachen linearen Regression kannst du die Regressionskoeffizienten  und
und  ganz leicht berechnen. Bevor du
ganz leicht berechnen. Bevor du  und
und  ausrechnen kannst, musst du aber noch kurz ein paar andere Werte ermitteln.
ausrechnen kannst, musst du aber noch kurz ein paar andere Werte ermitteln.
Zunächst berechnest du die Mittelwerte
 und
und  sowie die Standardabweichungen
sowie die Standardabweichungen
 und
und  des Prädiktors und des Kriteriums. In unserem Beispiel ist der Prädiktor
des Prädiktors und des Kriteriums. In unserem Beispiel ist der Prädiktor  der Ticketpreis und das Kriterium
der Ticketpreis und das Kriterium  die Anzahl der Gäste auf dem Festival.
die Anzahl der Gäste auf dem Festival.




Anschließend berechnest du die Kovarianz
 und die Korrelation
und die Korrelation
 .
.


Mit Hilfe dieser Werte kannst du nun die Regressionskoeffizienten bestimmen. berechnest du so:
berechnest du so:

Und auf  kommst du mit folgender Formel:
kommst du mit folgender Formel:

Damit hast du deine Regressionsgleichung erstellt. Sie lautet folgendermaßen:

In diese Formel könntest du nun einen Ticketpreis einsetzen, für den du die Gästezahl vorhersagen möchtest.
Umrechnung: Unstandardisiert / Standardisiert
Möchtest du statt der unstandardisierten Regressionsgleichung lieber die standardisierte Variante der Regressionsgleichung haben, dann musst du statt der b-Gewichte die  -Gewichte verwenden. Im Fall von nur einem Prädiktor entspricht das
-Gewichte verwenden. Im Fall von nur einem Prädiktor entspricht das  -Gewicht einfach der Korrelation zwischen dem Prädiktor und dem Kriterium. Im Fall von mehreren Prädiktoren rechnest du ein
-Gewicht einfach der Korrelation zwischen dem Prädiktor und dem Kriterium. Im Fall von mehreren Prädiktoren rechnest du ein  -Gewicht folgendermaßen in
-Gewicht folgendermaßen in  um:
um:
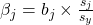
Dabei steht der Index  für den Prädiktor, für den du das
für den Prädiktor, für den du das  -Gewicht nach
-Gewicht nach  (oder andersherum) ausrechnen möchtest. Um die fertige Regressionsgleichung zu erhalten, musst du diesen Vorgang für jeden beteiligten Prädiktor wiederholen.
(oder andersherum) ausrechnen möchtest. Um die fertige Regressionsgleichung zu erhalten, musst du diesen Vorgang für jeden beteiligten Prädiktor wiederholen.
Noch mehr Regressionsanalyse?
Nun weißt du über die Regressionskoeffizienten und die Regressionsgleichung Bescheid! Wenn du noch mehr über andere Kennzahlen und Eigenschaften der Regressionsanalyse erfahren möchtest, dann schau doch mal hier vorbei: