In diesem Artikel erklären wir dir, was der Standardfehler ist und wie du ihn berechnest. Wir gehen zunächst auf die Bedeutung des Standardfehlers des Mittelwerts ein und besprechen anschließend die Berechnung anhand eines anschaulichen Beispiels.
Du möchtest das Thema noch schneller verstehen? Dann sieh dir unser Video an und erfahre in nur wenigen Minuten alles, was du darüber wissen musst.
Standardfehler – einfach erklärt
Der Standardfehler (engl. „standard error“ oder SE) ist ein Maß dafür, wie stark ein beobachteter Parameter – etwa der Mittelwert oder der Median – in einer Stichprobe durchschnittlich vom wahren Parameter der Grundgesamtheit abweicht.
In anderen Worten beschreibt der Standardfehler also, wie stark sich verschiedene Stichprobenmittelwerte aus der gleichen Grundgesamtheit unterscheiden.
-
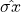– Geschätzter Standardfehler des Mittelwerts -
– (korrigierte) Standardabweichung der Messwerte in der Stichprobe 
Stichprobengröße
Der Standardfehler des Mittelwerts gibt uns Auskunft darüber, wie gut wir den wahren Mittelwert der Grundgesamtheit mit dem Mittelwert aus der Stichprobe schätzen können.
Der Standardfehler des Mittelwerts
Der bekannteste Standardfehler ist der Standardfehler des Mittelwerts. Häufig wird auch die englische Bezeichnung standard error of the mean (kurz: SEM) verwendet. Er gibt an, wie stark der beobachtete Mittelwert aus der Stichprobe durchschnittlich vom wahren Mittelwert der Grundgesamtheit abweicht. Er ist damit die Standardabweichung der Mittelwerte für alle möglichen Stichproben, die du aus der Grundgesamtheit ziehen kannst.
Die Formel zur Berechnung des Standardfehlers des Mittelwerts lautet: .
Beispiel SEM
Um das zu verdeutlichen, sehen wir uns ein Beispiel an: Wir möchten herausfinden, wie viele Stunden Personen durchschnittlich für eine Prüfung lernen. Wir befragen also 50 Leute nach ihrem Lernaufwand und berechnen die durchschnittliche Lernzeit pro Prüfung. Der erhaltene Stichprobenmittelwert ist eine gute Schätzung für die durchschnittliche Lerndauer in der Grundgesamtheit. Allerdings entspricht der Stichprobenmittelwert meist nicht perfekt dem wahren Mittelwert in der Grundgesamtheit. Das liegt daran, dass wir die Grundgesamtheit in einer kleinen Stichprobe nicht perfekt abbilden können. Würden wir beispielsweise noch eine zweite Gruppe von 50 Personen untersuchen, erhielten wir einen etwas anderen Stichprobenmittelwert als in der ersten Gruppe. Der Standardfehler gibt uns nun Auskunft darüber, wie stark sich die Mittelwerte verschiedener Stichproben durchschnittlich unterscheiden.
Standardabweichung des Mittelwerts
Um das noch etwas tiefer zu verstehen, stellen wir uns vor, wir würden immer wieder Gruppen von 50 Personen nach ihrer Lernzeit befragen. Die Mittelwerte der einzelnen Stichproben halten wir hierbei in einer Tabelle fest. Betrachten wir anschließend diese Tabelle, dann bilden die unterschiedlichen Stichprobenmittelwerte eine neue Verteilung. Aus dieser Verteilung könnten wir wiederum den Mittelwert und die Standardabweichung bestimmen. Die Standardabweichung dieser Verteilung entspricht dann dem gesuchten Standardfehler. Anders gesagt ist der Standardfehler also die Standardabweichung des Mittelwerts.
| Gruppe | 1 | 2 | 3 | 4 | 5 |
| Mittelwert (in Stunden) |
18 | 17,6 | 18,5 | 19,1 | 17,8 |
In der Praxis brauchst du jedoch nur eine einzige Stichprobe, um den Standardfehler berechnen zu können. Voraussetzung für die Berechnung ist, dass die Personen in deiner Stichprobe zufällig ausgewählt wurden. Du erhältst den Standardfehler, indem du die Standardabweichung deiner Messwerte durch die Wurzel deiner Stichprobengröße teilst. An der Formel siehst du, dass der Standardfehler kleiner wird, je größer deine Stichprobe ist. Mit zunehmender Stichprobengröße wird die Schätzung des wahren Mittelwerts mit dem Stichprobenmittelwert also zunehmend genauer.
-
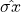– Geschätzter Standardfehler des Mittelwerts
-
– (korrigierte) Standardabweichung der Messwerte in der Stichprobe Stichprobengröße
Berechnung des Standardfehlers: Beispiel
Sehen wir uns nun die Berechnung an einem konkreten Beispiel an. Wir haben 50 Personen nach ihrer Lerndauer pro Prüfung befragt. Wir berechnen den Mittelwert der Messwerte und erhalten eine durchschnittliche Lerndauer von 18 Stunden pro Klausur. Falls du dir nochmal ansehen möchtest, wie man einen Mittelwert berechnet, sieh dir gerne unseren Artikel dazu an. Die Standardabweichung der Messwerte beträgt 6,3 Stunden. Diese Werte können wir nun in die Formel für den Standardfehler des Mittelwerts einsetzen.
Der Ergebnis ist 0,89. Durchschnittlich weicht die in der Stichprobe beobachtete mittlere Lerndauer also um 0,89 Stunden von der wahren durchschnittlichen Lerndauer ab.
Unterscheidung: Standardfehler und Standardabweichung
Es ist wichtig, dass du den Standardfehler des Mittelwerts nicht mit der Standardabweichung verwechselst. Um den Unterschied zwischen beiden Statistiken klar zu machen, sehen wir uns die Abgrenzung nochmal im Detail an: Der SEM beschreibt, wie stark beobachtete Mittelwerte um den wahren Mittelwert der Grundgesamtheit schwanken. Es geht hier folglich um die Streuung der Mittelwerte.
Die Standardabweichung ist hingegen ein Maß für die Streuung der Messwerte, das heißt wie gleich oder verschiedenartig die Messwerte in der Stichprobe sind. Aus allen Messwerten kannst du den Mittelwert berechnen.
Der Standardfehler gibt an, wie stark sich der Mittelwert der Stichprobe vom eigentlichen Mittelwert in der Grundgesamtheit unterscheidet. Auf Englisch heißt der Standardfehler „standard error of the mean“, oder abgekürzt SEM.
Weitere Standardfehler und Anwendung
In diesem Artikel haben wir uns vor allem mit dem Standardfehler des Mittelwerts beschäftigt. Der Standardfehler kann aber auch für andere Statistiken wie die Varianz oder die Korrelation berechnet werden. Eine verbreitete Anwendungsmöglichkeit ist das Bilden von Konfidenzintervallen. Wenn du mehr über Konfidenzintervalle erfahren möchtest, dann sieh dir gerne unser Video dazu an.
