Bestimmtheitsmaß

Bestimmtheitsmaß R² einfach erklärt

Das Bestimmtheitsmaß  (auch: Determinationskoeffizient, R squared) ist eine Kennzahl der Regressionsanalyse . Sie gibt dir Auskunft darüber, wie gut du die abhängige Variable mit den betrachteten unabhängigen Variablen vorhersagen kannst. In der Fachsprache sagt man, es gibt an, welchen Anteil der Varianz der abhängigen Variable durch die unabhängige(n) Variable(n) „aufgeklärt“ wird. Das Bestimmtheitsmaß kann Werte zwischen 0 und 1 annehmen. Prinzipiell stehen dabei höhere Werte für eine bessere Vorhersage der abhängigen Variable.

Wie hoch es sein soll, hängt dabei allerdings von den betrachteten Variablen und dem untersuchten Thema ab. Tendenziell überschätzt das Bestimmtheitsmaß zudem leicht den Anteil der aufgeklärten Varianz. Deshalb verwendet man das adjustierte Bestimmtheitsmaß , wenn man Aussagen aus einer Stichprobe auf die Grundgesamtheit übertragen möchte.

Bestimmtheitsmaß Herleitung 

Das Bestimmtheitsmaß zeigt den Anteil der aufgeklärten Varianz an der Gesamtvarianz der abhängigen Variable (AV).

Um diese Statistik zu verstehen, müssen wir uns  also nochmal die Bedeutung der Varianz ins Gedächtnis rufen: Grob gesagt beschreibt die Varianz, wie stark sich die Messwerte in einer Stichprobe unterscheiden. Eine kleine Varianz sagt aus, dass sich die Messwerte alle sehr ähneln. Eine große Varianz heißt hingegen, dass die Werte sehr unterschiedlich sind und weit verstreut liegen.

Stell dir nun vor, du betrachtest in einer Untersuchung die erreichte Punktzahl in einer Matheprüfung. Vermutlich werden nicht alle Personen in der Prüfung die gleiche Punktzahl erreicht haben. Stattdessen werden  einige werden besser, und andere schlechter abgeschnitten haben. Es gibt also Varianz in der erreichten Punktzahl.

Nun kann es verschiedene Gründe geben, warum Personen in der Prüfung mehr oder weniger Punkte erreicht haben. Beispielsweise könnte das Ausmaß der Vorbereitung einen Einfluss auf das Prüfungsergebnis haben. Ebenfalls könnte die Intelligenz oder das Vorwissen einer Person die Leistung beeinflussen. Und schließlich könnten Personen abgeschrieben, schlecht geschlafen oder vor der Prüfung sehr viel Kaffee getrunken haben, was ihre zusätzliche Punktzahl beeinflusst. All diese Gründe können dazu führen, dass Personen unterschiedliche Punktzahlen in der Prüfung erreichen. 

In einer Regressionsanalyse wählst du nun einzelne dieser möglichen Gründe als unabhängige Variablen aus. Von diesen Variablen vermutest du, dass sie einen besonders starken Einfluss auf die abhängige Variable „Punkte in der Matheprüfung“ haben könnten.

Dein Ziel ist es, mit Hilfe der unabhängigen Variablen möglichst gut zu erklären, warum sich die Punktzahlen verschiedener Personen in der Prüfung unterscheiden. In der Fachsprache sagt man, du möchtest möglichst viel Varianz der abhängigen Variable durch die unabhängige Variable „aufklären“. Du untersuchst also zum Beispiel, wie viel der Unterschiedlichkeit der erreichten Punktzahlen dadurch erklärt werden kann, dass Menschen unterschiedlich intelligent sind. 

Bestimmtheitsmaß Berechnung 

Das Bestimmtheitsmaß ist nun eine Kennzahl, die dir genau das verrät. Es gibt an, welcher Anteil der Varianz der Punktzahl (also der abhängigen Variablen) durch die Intelligenz (die unabhängige Variable) erklärt werden kann.

Um es zu berechnen, kannst du diese Formel verwenden: 

Du teilst also die aufgeklärte Varianz durch die gesamte Varianz der abhängigen Variable. Damit erhältst du, welcher Anteil an der Gesamtvarianz durch die unabhängigen Variablen aufgeklärt werden konnte.

Alternativ kannst du auch über die nicht aufgeklärte Varianz berechnen: 

Bei diesem Rechenweg ziehst du den Anteil der Varianz, der nicht aufgeklärt wurde, von 1 ab. Da sich die Anteile von aufgeklärter und nicht aufgeklärter Varianz zu 1 ergänzen, erhältst du auch über diesen Weg das Ergebnis für .

Beide Formeln liefern also das gleiche Ergebnis. Welchen Weg du zur Berechnung wählst, hängt meist einfach davon ab, welche Angaben du in der Aufgabe gegeben hast. Bei der einfachen linearen Regression kannst du das Bestimmtheitsmaß sogar noch einfacher berechnen: Hier erhältst du es, in dem du einfach den Korrelationskoeffizienten 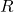quadrierst. 

Um das Konzept des Bestimmtheitsmaß möglichst einfach zu verdeutlichen, haben wir in diesem Beitrag ein Beispiel  gewählt, das einen kausalen Zusammenhang zwischen unabhängiger und abhängiger Variable nahe legt („Eine Person ist besser in der Prüfung, weil sie intelligenter ist“). Bitte beachte aber, dass du im Zuge einer Regressionsanalyse nicht einfach von einer Korrelation auf Kausalität schließen darfst! Ob das möglich ist, hängt immer von deinem gewählten Untersuchungsdesign (z.B. Experiment) ab.  

Bestimmtheitsmaß Interpretation

Da das Bestimmtheitsmaß einen Anteil von etwas ausdrückt, kann es Werte zwischen 0 und 1 annehmen. Größere Werte stehen hierbei für mehr aufgeklärte Varianz und somit für eine bessere Vorhersage der abhängigen Variable. 

Zwar spricht ein hohes Bestimmtheitsmaß für einen starken Zusammenhang zwischen unabhängiger und abhängiger Variable, das bedeutet jedoch im Umkehrschluss nicht, dass gar kein Zusammenhang besteht, wenn nahe oder gleich 0 ist. Das liegt daran, dass nur geeignet ist, um lineare Zusammenhänge abzubilden. Stehen deine Variablen also zum Beispiel in einem quadratischen oder exponentiellen Verhältnis zueinander, wird quasi 0 sein, obwohl die Variablen systematisch zusammenhängen. Um solche Fälle zu erkennen, hilft es sich Diagramme deiner Daten anzusehen. 

Generell kannst du das Bestimmtheitsmaß aber so interpretieren: Nehmen wir an, du erhältst ein Bestimmtheitsmaß von . Das bedeutet, dass 30 % der Varianz der abhängigen Variablen durch die unabhängige(n) Variable(n) aufgeklärt werden konnten. 70 % der Unterschiedlichkeit der Messwerte geht hingegen auf Einflüsse zurück, die wir in unserer Untersuchung nicht betrachtet haben. Diese Varianz aufgrund von unbekannten Einflüssen bezeichnen wir pauschal als „Fehler-„ oder als „Residualvarianz“. 

Wie hoch das Bestimmtheitsmaß mindestens sein soll, lässt sich nicht pauschal festlegen. Das hängt von verschiedenen Faktoren ab, beispielsweise in welchem Forschungsfeld du deine Untersuchung durchführst und wie viele unabhängige Variablen du gleichzeitig betrachtest. Wenn du dir unsicher bist, wie hoch in einem konkreten Fall sein sollte, dann schlage am besten in anderen Untersuchungen zu deinem Thema nach. 

Adjustiertes Bestimmtheitsmaß 

Nun weißt du bereits, wie man das Bestimmtheitsmaß in einer Stichprobe berechnet und interpretiert. Allerdings fällt das Bestimmtheitsmaß durch zufällige Fehler in Stichproben meistens etwas zu hoch aus. Wie stark diese Überschätzung ist, ist dabei von der Stichprobengröße und der Anzahl der betrachteten Variablen abhängig. Das ist vor allem ein Problem, wenn du Ergebnisse aus der Stichprobe auf die Grundgesamtheit übertragen möchtest. Deshalb gibt es eine Formel, mit der du die Überschätzung von korrigieren kannst. Die korrigierte Version des Bestimmtheitsmaßes wird adjustiertes Bestimmtheitsmaß  oder auch „adjusted squared multiple R“ genannt. 
Du berechnest es so: 

Residuen

Ein weiteres Wichtiges Thema der Regressionsanalyse sind die Residuen . Was Residuen sind und wie du sie berechnest, erfährst du in unserem Video dazu. Schau es dir unbedingt an damit du die Regressionsanalyse für deine nächste Prüfung verstehst!