Regressionsanalyse
Dieser Artikel hilft dir beim Einstieg in die Regressionsanalyse. Wir erklären dir, was die Regressionsanalyse ist, wofür du sie verwendest und wie du sie richtig interpretierst.
Du lernst lieber audiovisuell? Dann sieh dir unser Video an und verstehe dort noch schneller, was du über die Regressionsanalyse wissen musst.
Inhaltsübersicht
Regressionsanalyse einfach erklärt
Die Regressionsanalyse ist ein statistisches Analyseverfahren. Mit Hilfe der Regression kannst du untersuchen, wie gut du die Werte einer Variablen mit den Werten einer oder mehrerer anderer Variablen vorhersagen kannst. Dafür betrachtest du den Zusammenhang der Variablen und erstellst auf dieser Grundlage eine Vorhersagefunktion. Je stärker der Zusammenhang zwischen den Variablen ist, desto besser kannst du die eine durch die andere vorhersagen.
Die Variable, die vorhergesagt werden soll, nennt man abhängige Variable oder Kriterium. Die Variable, die zur Vorhersage des Kriteriums genutzt wird, bezeichnet man hingegen als unabhängige Variable oder als Prädiktor. Die Regressionsanalyse wird für verschiedene Zwecke verwendet. Neben der Vorhersage von neuen Werten wird sie auch dafür eingesetzt, um die Zusammenhänge zwischen verschiedenen Variablen näher zu untersuchen.
Regressionsanalyse Beispiel
Am einfachsten lässt sich die Regressionsanalyse an einem Beispiel erklären:
Stell dir vor, du möchtest einen Freund zum Geburtstag mit einem neuen Paar Schuhe überraschen. Leider kennst du jedoch seine Schuhgröße nicht und bist deshalb unsicher, welche Schuhe du genau kaufen sollst. Ihn direkt nach seiner Schuhgröße fragen möchtest du nicht, schließlich wäre dann die ganze Überraschung kaputt.
Also schmiedest du einen Plan:
Du kennst zwar nicht die Schuhgröße deines Freunds, dafür weißt du allerdings, wie groß er ist, nämlich 182 cm. Du vermutest, dass größere Personen tendenziell auch größere Schuhe tragen. Folglich möchtest du versuchen, die Schuhgröße deines Freunds mit Hilfe seiner Körpergröße zu schätzen. Um herauszufinden, wie stark die Schuhgröße einer Person mit ihrer Körpergröße zusammenhängt, führst du in deinem Umfeld eine Umfrage durch. Dabei sammelst du in einer Tabelle alle Informationen zur Körper- und Schuhgröße deiner Bekannten.
Und tatsächlich: Größere Personen haben in deiner Stichprobe tendenziell auch größere Füße. Wie stark der Zusammenhang zwischen Körper- und Schuhgröße ist, kannst du aus den Daten in deiner Tabelle berechnen. Dafür verwendest du die Produkt-Moment-Korrelation. In deiner Stichprobe beträgt die Korrelation
 .
.
Jetzt kennst du also die Körpergröße deines Freunds und weißt, wie stark die Körpergröße mit der Schuhgröße zusammenhängt. Mit Hilfe dieser Informationen kannst du nun schätzen, wie groß vermutlich die Schuhe deines Freunds sind – und das ganz ohne ihn zu fragen! Wie du diese Schätzung bei der Regressionsanalyse genau triffst, sehen wir uns im nächsten Abschnitt an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Regressionsgleichung
Um die Schätzung der Schuhgröße mathematisch durchzuführen, brauchst du bei der Regressionsanalyse eine Vorhersagefunktion. Diese Vohersagefunktion wird häufig auch Regressionsgleichung genannt. In die Regressionsgleichung kannst du jede beliebige Körpergröße einsetzen und erhältst als Ergebnis eine Schätzung für die Schuhgröße . Die Regressionsgleichung basiert dabei auf den Daten, die du in deiner Umfrage gesammelt hast. Hierbei ist besonders wichtig, wie stark die Variablen zusammenhängen, das heißt, wie stark sie miteinander korrelieren. Je ausgeprägter der Zusammenhang zwischen den Variablen, desto besser kannst du weitere Werte auf Grundlage der Messwerte deiner Stichprobe mit der Regressionsgleichung vorhersagen.
- Sammeln von Daten zu Variable A und B in einer Stichprobe
- Berechnung des Zusammenhangs von A und B auf Grundlage der Daten aus der Stichprobe
- Aufstellen der Regressionsgleichung und Vorhersage neuer Werte
Je nach dem, um welche Art der Regressionsanalyse es sich handelt, setzt sich die Vorhersagefunktion unterschiedlich zusammen. In unserem Beispiel der Schuhgrößenschätzung könnte sie zum Beispiel so aussehen:

 – Geschätzter Wert von Person
– Geschätzter Wert von Person  auf dem Kriterium
auf dem Kriterium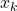 – Messwert von Person
– Messwert von Person  auf dem Prädiktor
auf dem Prädiktor
 ist hierbei die Variable, die du vorhersagen möchtest. Sie wird auch abhängige Variable oder Kriterium genannt. In unserem Beispiel ist die abhängige Variable die Schuhgröße.
ist hierbei die Variable, die du vorhersagen möchtest. Sie wird auch abhängige Variable oder Kriterium genannt. In unserem Beispiel ist die abhängige Variable die Schuhgröße.  ist hingegen die Variable, die du verwendest, um das Kriterium zu schätzen. Sie wird als unabhängige Variable oder als Prädiktor bezeichnet. In unserem Beispiel ist das die Körpergröße.
ist hingegen die Variable, die du verwendest, um das Kriterium zu schätzen. Sie wird als unabhängige Variable oder als Prädiktor bezeichnet. In unserem Beispiel ist das die Körpergröße.
Je nach dem, was für einen Wert du für 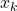 einsetzt, erhältst du eine andere Schätzung für
einsetzt, erhältst du eine andere Schätzung für  . Das heißt, abhängig davon, wie groß eine Person ist, fällt die Schätzung der Schuhgröße unterschiedlich aus. Setzt du etwa die Körpergröße deines Freunds, also 182 cm, ein, so liefert die Regressionsgleichung eine geschätzte Schuhgröße von 43,22.
. Das heißt, abhängig davon, wie groß eine Person ist, fällt die Schätzung der Schuhgröße unterschiedlich aus. Setzt du etwa die Körpergröße deines Freunds, also 182 cm, ein, so liefert die Regressionsgleichung eine geschätzte Schuhgröße von 43,22.

Wie du die Vorhersagefunktion genau aufstellst und interpretierst, erfährst du hier.
Residuen
Nun hast du mit Hilfe eines Werts auf dem Prädiktor eine Schätzung darüber getroffen, welchen Wert die entsprechende Person auf dem Kriterium haben könnte. Der vorhergesagte Kriteriumswert wird dabei jedoch fast nie genau dem Wert entsprechen, den die Person tatsächlich auf der abhängigen Variablen hat. So kann es zum Beispiel sein, dass du deinem Freund zwar die Schuhgröße 43,22 vorhergesagt hast, er aber in Wahrheit eigentlich Schuhgröße 44 trägt. Dass deine Vorhersage ein wenig vom wahren Wert abweicht, liegt daran, dass deine Schätzung zwar so gut wie möglich, aber meist eben nicht perfekt ist. Häufig wirst du mit deiner Vorhersage also ein wenig daneben liegen. Diese Abweichung zwischen dem vorhergesagten Wert und dem wahren Wert einer Person auf der abhängigen Variable wird als Residuum bezeichnet.
Regressionsgerade
Im Fall der einfachen linearen Regression kannst du die Regressionsanalyse grafisch mit der Regressionsgerade darstellen. Die Regressionsgerade ist die Linie, auf der alle vorhergesagten Werte der Regressionsanalyse liegen. Sie wird nach einem bestimmten Prinzip in die Punktwolke aus den verschiedenen beobachteten Messwerten eingezeichnet. Dabei soll versucht werden, dass die Gerade insgesamt möglichst nah an allen Messwertpunkten liegt. Mathematisch wird das erreicht, indem man die sogenannte Methode der kleinsten Quadrate anwendet.
An der Regressionsgerade kannst du optisch erkennen, wie stark der Zusammenhang zwischen Prädiktor und Kriterium ist: Fällt die Gerade ab, ist der Zusammenhang negativ, steigt sie hingegen an, ist die Korrelation positiv.
Regression interpretieren
Um die Regression
zu interpretieren, kannst du ganz verschiedene Kennwerte berechnen. Besonders häufig wird das Bestimmtheitsmaß
(auch: Determinationskoeffizient)  betrachtet. Es gibt dir Auskunft darüber, wie gut du das Kriterium mit dem Prädiktor oder den Prädiktoren vorhersagen kannst. Es kann Werte zwischen 0 und 1 annehmen, wobei höhere Werte für eine bessere Vorhersage sprechen. Berechnen kannst du das Bestimmtheitsmaß, in dem du den (multiplen) Korrelationskoeffizienten
betrachtet. Es gibt dir Auskunft darüber, wie gut du das Kriterium mit dem Prädiktor oder den Prädiktoren vorhersagen kannst. Es kann Werte zwischen 0 und 1 annehmen, wobei höhere Werte für eine bessere Vorhersage sprechen. Berechnen kannst du das Bestimmtheitsmaß, in dem du den (multiplen) Korrelationskoeffizienten 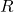 quadrierst. Inhaltlich beschreibt das Bestimmtheitsmaß, welchen Anteil der Varianz des Kriteriums die Prädiktoren insgesamt aufklären können. Wenn du mehr darüber erfahren möchtest, was das genau bedeutet, dann sieh dir gerne unseren Beitrag zum Bestimmtheitsmaß
an.
quadrierst. Inhaltlich beschreibt das Bestimmtheitsmaß, welchen Anteil der Varianz des Kriteriums die Prädiktoren insgesamt aufklären können. Wenn du mehr darüber erfahren möchtest, was das genau bedeutet, dann sieh dir gerne unseren Beitrag zum Bestimmtheitsmaß
an.
Korrelation und Kausalität bei der Regressionsanalyse
Du hast nun bereits gelernt, dass die Vorhersage von Werten in der Regressionsanalyse auf der Korrelation zwischen Variablen basiert. Wichtig ist, dass eine Korrelation zwischen zwei Variablen nicht aber unbedingt Kausalität bedeutet. Das heißt: Nur weil höhere Werte auf der einen Variable mit höheren Werten auf der anderen Variable einhergehen, bedeutet das nicht, dass die Werte auf der einen Variable ansteigen, weil die Werte auf der anderen Variable besonders hoch sind.
Beispielsweise wurde im letzten Jahrhundert eine Korrelation zwischen der Anzahl von Störchen und der Geburtenrate in einer Region beobachtet. Allerdings ist es natürlich nicht so, dass irgendwo mehr Kinder geboren werden, weil es dort mehr Störche gibt. Viel mehr sorgten Drittvariablen wie die Industrialisierung dafür, dass in einigen Regionen sowohl die Geburtenrate als auch die Anzahl der Störche absank, was zu der beobachteten Korrelation führte. Ein kausaler Ursache-Wirkung-Zusammenhang lag aber natürlich nicht vor.
Du siehst, dass man bei der Interpretation von Korrelationen also vorsichtig sein muss. Dass du mit deinen Daten eine Regressionsanalyse rechnen kannst, ist hierbei niemals ein Beweis für Kausalität zwischen deinen Variablen. Kausalität kannst du nur sicher mit Hilfe von experimentellen Untersuchungsdesigns feststellen, nie jedoch alleine mit bestimmten statistischen Analyseverfahren.
Arten der Regressionsanalyse
Am Ende dieses Artikels hast du nun einen Überblick darüber, was die Regressionsanalyse ist und wie sie funktioniert. Allerdings gibt es aber nicht nur eine einzige Regressionsanalyse, sondern eine ganze Gruppe von verschiedenen Regressionsarten. Die Arten der Regressionsanalysen unterscheiden sich beispielsweise darin, wie viele Prädiktoren betrachtet werden oder welche Eigenschaften die Variablen haben. Hier siehst du eine Auflistung einiger der bekanntesten Regressionsanalysen. Wenn du über eine Art davon mehr erfahren möchtest, dann sieh dir gerne unseren separaten Beitrag dazu an:
- Einfache lineare Regression
- Multiple lineare Regression
- Logistische Regression
- Multivariate Regression
