t Test
Was ist eigentlich der t Test und wie führt man ihn richtig durch? Solltest du dir diese Fragen stellen, findest du alle relevanten Antworten in diesem Beitrag. Nach einer kurzen Einführung in die unterschiedlichen Arten und Subkategorien des t Tests, lernst du anhand verschiedener Beispiele, wie sich der t Test aktiv durchführen lässt. Außerdem zeigen wir dir, wie du in diesem Kontext richtig mit der Verteilungstabelle arbeitest und wie du die Ergebnisse des t Tests final interpretieren kannst.
Wenn du dir das Thema lieber visuell aneignen willst, ist unser Lernvideo genau das Richtige für dich!
Inhaltsübersicht
t Test einfach erklärt
Was ist der t Test? Der t Test ist ein Verfahren, das für Untersuchungen mit t-verteilten Datensätzen den Hypothesentest durchführen kann. Der t Test besteht aus mehreren Rechenschritten, wobei die Berechnung der Teststatistik über deren Formel und das Nachschlagen in der t-Verteilungstabelle die wesentlichen Aspekte darstellen. Es gibt zwei Möglichkeiten, wie die Testentscheidung beim t Test ausfallen kann: der über die Teststatistik ermittelte t Wert kann einerseits niedriger sein als der in der Verteilungstabelle abgelesene kritische Wert. Andersherum kann der über die Teststatistik ermittelte t Wert auch größer ausfallen als der in der Verteilungstabelle abgelesene kritische Wert.
Das wirkt sich folgendermaßen auf die Kernaufgabe des t Tests aus: tritt der erste Fall ein, kannst du die Nullhypothese einer Untersuchung ablehnen. Tritt hingegen der zweite Fall ein, musst du die Nullhypothese vorläufig beibehalten. Bevor wir genauer auf die Berechnung der relevanten Werte eingehen, lernst du zunächst einmal die Arten des t Test genauer kennen.
Student t Test
Der sogenannte Student t Test unterteilt sich in folgende Teilbereiche: den Einstichprobentest sowie den Zweistichprobentest. Der Einstichprobentest untersucht, ob der Mittelwert einer Stichprobe überzufällig von einem extern gegebenen, anderen Wert abweicht. Er lässt sich linksseitig, rechtsseitig und zweiseitig durchführen. Welche Art der Durchführung man für den Einstichprobentest wählt, hängt hauptsächlich von der Richtung der Hypothesen ab. Gerichtete Hypothesen testest du in der Regel einseitig, ungerichtete hingegen zweiseitig.
Der Zweistichprobentest wird dann angewendet, wenn zwei Stichproben und deren zugehörige Mittelwerte miteinander verglichen werden sollen. Dabei kannst du zwischen unverbundenen und verbundenen Stichproben unterscheiden. Ein Beispiel für den unverbundenen Test könnte eine Untersuchung sein, die zwei verschiedene Stichproben unter Probanden in unterschiedlichen Städten erhebt. Der verbundene oder auch abhängige Test kann beispielsweise dann zum Einsatz kommen, wenn eine zeitliche Trennung zwischen den Stichproben (z.B. 2013 und 2019) vorliegt, die Probanden aber dieselben bleiben.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Einstichproben t Test
Um in eine Untersuchung einzusteigen, müssen immer Hypothesen gegeben sein. Diese geben dir am Anfang der Untersuchung bereits einen Anhaltspunkt, mit welcher Art von Test du sie später im Forschungsprozess überprüfen kannst:
t Test linksseitig: t Test rechtsseitig:
 :
: 
 :
: 
 :
: 
 :
: 
t Test zweiseitig:
 :
: 
 :
: 
Neben der Ausrichtung der Hypothesen ist ein weiterer wichtiger Faktor des Einstichproben-t-Tests die Formel der Teststatistik. Sie gibt am Ende die Prüfgröße aus, die mit dem kritischen Wert verglichen wird und entscheidet, ob die Nullhypothese abgelehnt wird oder vorläufig bestehen bleibt. Die Formel der Teststatistik sieht folgendermaßen aus:

t Test Beispiel
Damit du eine Idee davon bekommst, wie die jeweiligen Testarten in der Praxis aussehen können, stellen wir dir in diesem Abschnitt jeweils ein Beispiel zum zweiseitigen, rechtsseitigen und linksseitigen Hypothesentest vor. Während die ersten beiden Beispiele exemplarisch mit gegebenen Werten behandelt werden, rechnen wir für das dritte Beispiel eines linksseitigen t Tests alles einmal komplett durch, um die ganze Durchführung nachvollziehbar zu präsentieren.
Zweiseitiger t Test
Der zweiseitige t Test testet in keine spezifische Richtung, sondern will nur eine Abweichung vom Normalzustand, der in der H0 festgehalten wird, nachweisen. Ein Indikator dafür, dass du einen zweiseitigen Hypothesentest durchführen solltest, ist das Vorliegen eines ungerichteten Hypothesenpaars.
Zum Verständnis verdeutlichen wir das Ganze an einem Beispiel: Ein Unternehmen zweifelt an, ob seine Maschinen die Verpackungen für Cornflakes mit der richtigen Menge befüllen und will dies testen. Sowohl zu wenig als auch zu viel Inhalt würden das Unternehmen nämlich vor Probleme stellen. Daher testet man in solch einem Fall nicht in eine spezifische Richtung, sondern in beide Richtungen.
Beim Testen von Hypothesen über den t Test muss man im Laufe des Prozesses einige Werte ermitteln, um am Ende eine finale Entscheidung treffen zu können. Folgende Werte sind für die Durchführung eines t Tests notwendig:
- Mittelwert/Erwartungswert
- Vergleichswert

- Standardabweichung
- Stichprobengröße
- Teststatistik: Prüfgröße
- kritische(r) Wert(e) (1 beim einseitigen t Test, 2 beim zweiseitigen t Test)
Die Werte 1-4 musst du berechnen, um sie anschließend in die Formel der Teststatistik einzusetzen. Die Teststatistik ergibt dir mit Wert 5 die Prüfgröße, die du zuletzt mit dem kritischen Wert (Wert 6) vergleichst. Diesen gewinnst du wiederum aus der t-Verteilungstabelle.
Für die Verpackungsbefüllung in einer Cornflakesfabrik würdest du mit den Werten exemplarisch so arbeiten.







Für den zweiseitigen Test musst du wie bereits erwähnt zwei kritische Werte ermitteln. Auf Grundlage der Freiheitsgrade und dem Signifikanzniveau, die für dieses Beispiel bei  und
und  liegen, kannst du hier die beiden kritischen Werte -2,093 und 2,093 ablesen. Der kritische Wert grenzt immer den Annahmebereich der Nullhypothese von Ablehnungsbereich ab. Da der Wert der Teststatistik außerhalb des Intervalls liegt, das die beiden Werte gemeinsam aufspannen, kann die Nullhypothese abgelehnt werden und somit behauptet werden, dass die Maschinen tatsächlich die Verpackungen falsch befüllen.
liegen, kannst du hier die beiden kritischen Werte -2,093 und 2,093 ablesen. Der kritische Wert grenzt immer den Annahmebereich der Nullhypothese von Ablehnungsbereich ab. Da der Wert der Teststatistik außerhalb des Intervalls liegt, das die beiden Werte gemeinsam aufspannen, kann die Nullhypothese abgelehnt werden und somit behauptet werden, dass die Maschinen tatsächlich die Verpackungen falsch befüllen.
Einseitiger t Test
Beim einseitigen Test unterscheidet man noch spezifischer zwischen dem rechtsseitigen und dem linksseitigen t Test. Den rechtsseitigen t Test führt man in Fällen durch, in denen man annimmt, dass die eigene, in der  verankerte Annahme höher/größer ist als der Wert, den die
verankerte Annahme höher/größer ist als der Wert, den die  repräsentiert. Den linksseitigen wendet man hingegen dann an, wenn man vermutet, dass die eigene Annahme einen niedrigeren/kleineren Wert annimmt als der Wert, den die
repräsentiert. Den linksseitigen wendet man hingegen dann an, wenn man vermutet, dass die eigene Annahme einen niedrigeren/kleineren Wert annimmt als der Wert, den die  repräsentiert.
repräsentiert.
rechtsseitiger Test
Stell dir vor du liest einen Zeitungsartikel, in dem behauptet wird, dass die durchschnittliche Körpergröße deutscher Männer bei 173 cm liegt. Auf Basis deiner eigenen Erfahrungen bzw. deines Vorwissens zweifelst du diese Aussage an, denn du vermutest dass deutsche Männer im Durchschnitt deutlich größer sind als 173 cm. Willst du deine Annahme auch begründen, würdest du in diesem Fall deine eigene Hypothese aufstellen und im Anschluss eben einen rechtsseitigen t Test durchführen, durch den du auf folgende Werte kommst.







Für dieses Beispiel ergibt sich über die Freiheitsgrade von  und das Signifikanzniveau von
und das Signifikanzniveau von  ein kritischer Wert von 1,660. Als Annahmebereich wird daher
ein kritischer Wert von 1,660. Als Annahmebereich wird daher ![Rendered by QuickLaTeX.com [-\infty; 1,660]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3fa00c31f0393c9f73a29f0d0399af60_l3.png) festgelegt. Das bedeutet, dass für alle Werte der Teststatistik über 1,660 die Nullhypothese abgelehnt wird.
festgelegt. Das bedeutet, dass für alle Werte der Teststatistik über 1,660 die Nullhypothese abgelehnt wird.
Für dieses Beispiel schließt du also, dass die Nullhypothese abgelehnt wird. Du kannst daher deine These bestätigen und behaupten, dass Männer im Durchschnitt in Deutschland größer als 173 cm sind.
linksseitiger Test
Anhand des linksseitigen t Tests soll nun einmal von vorne bis hinten demonstriert werden, wie der t Test durchzuführen ist. Für das Beispiel begeben wir uns in die Welt des Profifußballs. Jahrelang hielt sich in den höheren deutschen Fußballligen die Faustregel, dass 40 Punkte einer Mannschaft den Klassenerhalt sichern können. Die Vereine wollten natürlich nichts anbrennen lassen und sich zu früh in Sicherheit wägen. Trotzdem wollen wir mit dem t Test prüfen, ob dieser Wert nicht deutlich zu hoch angesetzt ist.
Die Untersuchungshypothesen, die wir über den t Test prüfen wollen, lauten daher:
 : weniger als 40 Punkte reichen im Durchschnitt zum Klassenerhalt
: weniger als 40 Punkte reichen im Durchschnitt zum Klassenerhalt 
 : ab 40 Punkten ist der Klassenerhalt im Durchschnitt gesichert
: ab 40 Punkten ist der Klassenerhalt im Durchschnitt gesichert 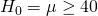
Teststatistik berechnen
Unser Datensatz besteht aus Punktzahlen von Mannschaften, die in den letzten Jahren den 15. Platz in der Tabelle belegt haben, und somit den letzten Platz, mit dem der Klassenerhalt sicher garantiert ist. Unser Datensatz sieht also folgendermaßen aus:
37 38 38 34 40 36 36 34 37 34 31 33 38 36 33 32 35 37 37 36 32
In einem ersten Schritt bestimmt man den Mittelwert der Stichprobe, der nach Aufsummierung aller Werte und Division durch die Anzahl aller Werte bei 35,43 liegt.
Danach bestimmt man die einzelnen Abweichungen von Mittelwert, die man für die Bestimmung der Standardabweichung braucht.
1,57 2,57 2,57 -1,43 4,57 0,57 0,57 -1,43 1,57 -1,43 -4,43 -2,43 2,57 0,57 -2,43 -3,43 -0,43 1,57 1,57 0,57 -3,43
Diese quadriert man nun einzeln und zählt sie dann zusammen, sodass man auf 113,14 kommt. Um die Varianz der Stichprobe zu erhalten, muss man jetzt nur noch durch  , also die Größe der Stichprobe, teilen. Es ergibt sich für die Varianz dann folgendes Ergebnis:
, also die Größe der Stichprobe, teilen. Es ergibt sich für die Varianz dann folgendes Ergebnis: 
Daraus kann man dann ganz leicht die für die Formel benötigte Standardabweichung berechnen:


Nach diesen Schritten haben wir alle Werte zusammen, die wir für die Formel der Teststatistik brauchen.







t Wert berechnen
Mit dem Wert der Teststatistik alleine kann man das Testen der Hypothesen jedoch noch nicht als abgeschlossen ansehen. Man benötigt zusätzlich den kritischen t Wert, der Annahme- und Ablehnungsbereich der Nullhypothese voneinander abtrennt. Im Falle des zweiseitigen t Tests werden natürlich zwei kritische t Werte benötigt, um die Bereiche voneinander abzugrenzen.
Diese Werte musst du glücklicherweise gar nicht berechnen. Stattdessen kannst du sie mithilfe des Signifikanzniveaus und der Freiheitsgrade ganz einfach in der t-Verteilungstabelle ablesen.
t Test Tabelle
Die Tabelle der t-Verteilung besitzt zwei Spalten: auf der horizontalen Spalte findest du die Ausprägung P. Hier liest du den Umkehrwert deines gegebenen Signifikanzniveaus ab. Da du im Regelfall mit einem Signifikanzniveau von 5% bzw.  arbeitest, kannst du jeweils beim linksseitigen und rechtsseitigen t Test mit dem Wert 0,95 für die horizontale Achse arbeiten. Beim beidseitigen t Test weicht die Herangehensweise für die Tabelle leicht ab, da der Annahmebereich mittig liegt und somit zwei kritische t Werte bestimmt werden müssen. Das Signifikanzniveau liegt daher immer noch bei 5%, wird aber auf beide Seiten aufgeteilt, was zur Folge hat, dass die Grenzen bei 2,5% und 97,5% liegen. Man arbeitet in so einem Fall daher auf der horizontalen Achse mit dem Wert 0,975.
arbeitest, kannst du jeweils beim linksseitigen und rechtsseitigen t Test mit dem Wert 0,95 für die horizontale Achse arbeiten. Beim beidseitigen t Test weicht die Herangehensweise für die Tabelle leicht ab, da der Annahmebereich mittig liegt und somit zwei kritische t Werte bestimmt werden müssen. Das Signifikanzniveau liegt daher immer noch bei 5%, wird aber auf beide Seiten aufgeteilt, was zur Folge hat, dass die Grenzen bei 2,5% und 97,5% liegen. Man arbeitet in so einem Fall daher auf der horizontalen Achse mit dem Wert 0,975.
Zusammen mit den Freiheitsgraden (Stichprobengröße n-1) kannst du so für alle unsere Beispiel die jeweiligen kritischen Werte ablesen. Für unser Beispiel liegt demnach der zugehörige kritische Wert für  Freiheitsgrade und einem Signifikanzniveau von
Freiheitsgrade und einem Signifikanzniveau von  bei -1,725.
bei -1,725.
t Test Interpretation
Wenn du die kritischen Werte dann mit den bereits zuvor berechneten Werten der Teststatistik vergleichst, kannst du eine fundierte Entscheidung über die vorläufige Beibehaltung oder Ablehnung der Nullhypothese treffen. Da der kritische t Wert immer einen kritischen Bereich abgrenzt, kannst du dir folgende Faustregel merken: liegt die Teststatistik innerhalb des kritischen Bereichs, kannst du die Nullhypothese zugunsten der  ablehnen. Fällt die Teststatistik stattdessen in den Annahmebereich, dann bleibt die Nullhypothese vorläufig bestehen, da sie durch die
ablehnen. Fällt die Teststatistik stattdessen in den Annahmebereich, dann bleibt die Nullhypothese vorläufig bestehen, da sie durch die  nicht widerlegt werden konnte.
nicht widerlegt werden konnte.
Für das Beispiel liegt der Vergleichswert der Teststatistik mit -9,03 deutlich außerhalb des Annahmebereichs, weshalb wir die Nullhypothese ablehnen und behaupten können, dass der durchschnittliche Wert, mit dem der Klassenerhalt gesichert werden kann, unterhalb der 40 Punkte Marke liegt.
