Clausius-Clapeyron-Gleichung
Die Clausius-Clapeyron-Gleichung wurde von Benoit Clapeyron entworfen und später von Rudolf Clausius weiterentwickelt. Mit Hilfe der Claudius-Clapeyron-Gleichung lässt sich die Siedepunktskurve in Phasendiagrammen berechnen. In diesem Beitrag lernst du, wie du die Claudius-Clapeyron-Gleichung herleitest und anwendest.
Inhaltsübersicht
Herleitung der Clausius-Clapeyron-Gleichung
Das wohl bekannteste aller Phasendiagramme ist das des Wassers. Neben den drei Phasen fest, flüssig und gasförmig, existieren auch drei Kurven, die die Phasenübergänge markieren: die Sublimations-, die Schmelz- und die Dampfdruckkurve. Um einen Ansatz zu erstellen, der uns später eine Berechnung zu einer dieser Kurven ermöglicht, wenden wir uns zuerst der Clapeyron-Gleichung zu. Die Überlegung dabei ist, dass die chemischen Potentiale beider beteiligter Phasen entlang der Phasengrenzen im Gleichgewicht sind.

Wanderst du zum Beispiel die Dampfdruckkurve entlang, wären die beiden beteiligten Phasen a und b die flüssige und die gasförmige. Die Potentiale hängen von Temperatur und Druck ab und heißen klein  .
.
Auch wenn sich Druck und Temperatur nur minimal ändern, gilt die Gleichung immer entlang der Kurven. Um jetzt herauszufinden, wie wir die Steigung der Phasengrenzlinien beschreiben können, verwenden wir eine altbekannte mathematische Schreibweise. Die Funktion dp nach dT:

Das bedeutet, dass entlang der Phasenübergänge nicht nur die chemischen Potentiale gleichbleiben, sondern auch ihre Veränderungen. Deshalb lautet unsere zweite Formel:

Weiterentwicklung der Clapeyron-Gleichung
Wenn wir uns an die Grundgleichungen der Thermodynamik erinnern, lässt sich die Änderung von durch folgende Gleichung beschreiben:

Das S steht für die Entropie und das V für Volumen. Im Index steht das kleine m für molar.
1.Schritt: Einsetzen
Das kannst du ganz einfach in  einsetzen:
einsetzen:

2.Schritt: Sortieren
Und anschließend sortieren:

3.Schritt: Ausklammern
Dann noch links dT und rechts dp ausklammern:

4.Schritt: Umstellen
Super, jetzt können wir so umstellen, dass sich für unser dp nach dT die Differenz der Entropie durch die Differenz des Volumens ergibt:

Und siehe da, schon hast du die Clapeyron-Gleichung hergeleitet! Das Besondere an dieser Gleichung ist, dass sie für jedes Phasengleichgewicht eines reinen Stoffes gilt!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Von der Clapeyron-Gleichung zur Clausius-Clapeyron-Gleichung
Die von dem Émile Clapeyron und Rudolf Clausius entwickelte Formel kann den Verlauf einer Siedepunktskurve in einem Phasendiagramm berechnen. Sie ist eine Spezialform der davor hergeleiteten Clapeyron Gleichung. Diese Gleichung liefert die Steigung aller Phasengrenzlinien in einem p-T-Diagramm eines Reinstoffsystems, kann jedoch für reversible Vorgänge mit der Clausius Clapeyron Gleichung spezifiziert werden.
Vorgänge, die man umkehren kann, nennt man reversibel. Die Entropie lässt sich dabei aus derjenigen Wärmemenge berechnen, die umgesetzt wird. Wir nennen sie  . Bleibt der Druck währenddessen gleich, spricht man von einem isobaren Vorgang und die Wärmemenge entspricht der Änderung der molaren Enthalpie
. Bleibt der Druck währenddessen gleich, spricht man von einem isobaren Vorgang und die Wärmemenge entspricht der Änderung der molaren Enthalpie  H.
H.  Sm entspricht also der Wärmemenge durch die Temperatur beziehungsweise der Änderung der molaren Enthalpie durch die Temperatur.
Sm entspricht also der Wärmemenge durch die Temperatur beziehungsweise der Änderung der molaren Enthalpie durch die Temperatur.

Damit gelangen wir direkt zur Clausius Clapeyron Gleichung, die ein Sonderfall der Clapeyron-Gleichung ist. Diese erlaubt uns eine Berechnung für den Verlauf der Phasengrenze zwischen flüssiger und gasförmiger Phase aufzustellen. In der thermodynamisch korrekten Version lautet die Gleichung:

Abgewandelte Form der Clausius-Clapeyron-Gleichung
Normalerweise nutzt man aber eine leicht abgewandelte Form,
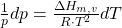
weil das molare Volumen eines Gases, das der Flüssigkeit meist deutlich übersteigt. In dieser Gleichung wird die eigentliche Differenz  V der beiden Volumina durch das des Gases ersetzt. Außerdem wird ein ideales Gas angenommen, dessen molares Volumen folgende Zustandsgleichung erfüllt:
V der beiden Volumina durch das des Gases ersetzt. Außerdem wird ein ideales Gas angenommen, dessen molares Volumen folgende Zustandsgleichung erfüllt:

Das R steht hierbei für die universelle Gaskonstante mit dem Wert von R = 8,314462 J mol -1 K -1
Integrierte Form der Clausius-Clapeyron-Gleichung
Außerdem gibt es die sogenannte integrierte Form der Clausius-Clapeyron-Gleichung. Diese ermöglicht es einen gegebenen Sättigungsdampfdruck p1 und eine Temperatur T1 mit zwei weiteren Werten p2 und T2 an einem anderen Punkt der Dampfdruckkurve zu vergleichen, beziehungsweise zu errechnen.

Mit ihr hast du nun auch die letzte der drei wichtigen Versionen der Clausius Clapeyron Gleichung kennengelernt. Falls dir also ihre Herleitung über die Clapeyron Gleichung in einer Aufgabe begegnen sollte, kannst du diese Schritt für Schritt erklären und anschließend Werte berechnen.









