Gibbssche Phasenregel
Ein sehr wichtiges Thema in der Thermodynamik für Flüssigkeiten, Gase oder Festkörpern ist die Gibbssche Phasenregel. Sie besagt, dass im thermodynamischen Gleichgewicht eine maximale Anzahl an Phasen gleichzeitig für ein Stoffsystem existieren kann. In unserem Videobeitrag lernst du die Phasenregeln anhand eines Beispiels in unter 5 Minuten kennen.
Inhaltsübersicht
Definition der Gibbsschen Phasenregel
Die Gibbssche Phasenregel beschreibt in der Thermodynamik einen Zusammenhang zwischen der Anzahl der Phasen in einem Gleichgewicht, den Komponenten des Systems und der Anzahl der thermodynamischen Freiheitsgrade. Sie besagt, dass in einem thermodynamischen Gleichgewicht nicht beliebig viele Phasen gleichzeitig vorliegen können. Außerdem können mit der Regel die Freiheitsgrade für einen Punkt im Zustandsdiagramm bestimmt werden.
Grundlagen der Gibbsschen Phasenregel
Zunächst einmal muss ein Stoff oder ein Stoffgemisch vorliegen. Dieses besteht aus K Komponenten und P Phasen. Außerdem hat es F thermodynamische Freiheitsgrade. Das ist die Anzahl der Zustandsgrößen, die geändert werden können, ohne, dass sich die Zahl der Phasen P im thermodynamischen Gleichgewicht in dem Stoffsystem verändert. Zustandsgrößen wären zum Beispiel Druck, Temperatur, Volumen, Teilchenanzahl, Entropie und so weiter. Für Gase und Flüssigkeiten lautet die Gibbssche Phasenregel:
F = K – P + 2
Für einen Feststoff ändert sich die Regel ein wenig, indem die 2 durch eine 1 ersetzt wird:
F = K – P + 1
Das liegt daran, dass eine Änderung des Druckes in Feststoffen keine großen Auswirkungen hat.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Gibbssche Phasenregel an einem Beispiel
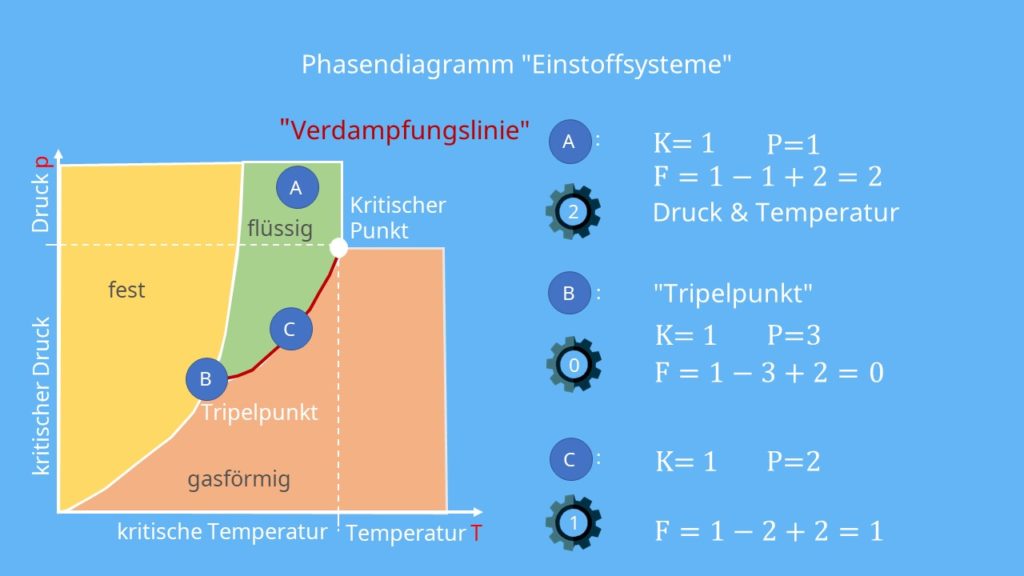
Am Beispiel eines Phasendiagramms von einem Einkomponentensystem soll die Formel erklärt werden. Eine Einführung zu Phasendiagrammen von Einstoffsystemen findest du in dem Kapitel zum Phasendiagramm Wasser. In einem solchen Diagramm werden nur die Zustandsgrößen Druck p und Temperatur T für die Beschreibung von Phasen eines Stoffes betrachtet. Ein vereinfachtes p-T-Diagramm sieht allgemein wie folgt aus:
Es liegen alle drei Aggregatzustände fest, gasförmig und flüssig vor. Nun wählen wir drei Punkte in diesem Diagramm aus. Diese wollen wir dann bezüglich ihrer Freiheitsgrade mit Hilfe der Gibbsschen Phasenregel untersuchen. Der erste Punkt A liegt im flüssigen Bereich, der zweite B im Tripelpunkt un den letzten C wählen wir auf die Dampfdruckkurve, welche auch als Siedepunktskurve bezeichnet wird.
Flüssiger Bereich
Der Punkt A liegt auf keiner der drei Übergangslinien. Er befindet sich mitten im Bereich der flüssigen Phase, sodass in der Phasenregel P = 1 ist. Außerdem behandeln wir ein Einnkomponentensystem, weshalb für K auch eins eingesetzt werden kann. Da wir keinen Festkörper anschauen, lautet die korrekte Gibbssche Phasenregel:
F = 1 – 1 + 2 = 2
Für den Punkt A ergeben sich also zwei Freiheitsgrade. Das bedeutet, dass es zwei Zustandsgrößen gibt, die man unabhängig voneinander in weiten Bereichen ändern kann, ohne dass sich P die Phase ändert.
Tripelpunkt
Der Punkt B liegt im Tripelpunkt des p-T-Diagramms. Hier koexistieren alle drei Phasen. Somit ergibt sich die Gibbssche Phasenregel als:
F = 1 – 3 + 2 = 0
Ein thermodynamischer Freiheitsgrad von 0 bedeutet, dass keine Variation der Größen Druck oder Temperatur möglich ist, ohne die Phasen mit zu verändern. Beispielsweise liegt der Tripelpunkt von Kohlenstoffdioxid genau bei 216,55K, was  entspricht und 5180hPa. Eine Abweichung von diesen Zahlen resultiert in einer Reduzierung der Anzahl der existierenden Phasen.
entspricht und 5180hPa. Eine Abweichung von diesen Zahlen resultiert in einer Reduzierung der Anzahl der existierenden Phasen.
Siedepunktskurve
Der letzte Punkt C liegt auf einer der Phasengrenzlinien, nämlich der Siedepunktskurve. Da hier zwei Phasen koexistieren, wird in der Gibbsschen Phasenregel zwei für P eingesetzt. K bleibt hingegen gleich eins. Daraus ergibt sich:
F = 1 – 2 + 2 = 1
Ein Freiheitsgrad von eins bedeutet, dass eine der Zustandsgrößen Druck oder Temperatur verändert werden kann, ohne dass sich die Anzahl und die Art, der im Gleichgewicht existierenden Phasen, ändert.
Gibbssche Phasenregel Zusammenfassung
Nach der Betrachtung der drei Fälle fällt auf, dass zwei Zustandsgrößen ausreichen, um einen Gleichgewichtszustand eindeutig zu beschreiben. Die Größen sind in diesem Fall Druck und Temperatur. Zusätzlich kannst du dir merken, dass in einem Einkomponentensystem maximal drei Phasen gleichzeitig existieren können und damit, laut der Gibbsschen Phasenregel, die thermodynamischen Freiheitsgrade immer gleich oder größer als null sein müssen.