Flächenpressung
In diesem Beitrag wird das Thema der Flächenpressung behandelt. Dabei werden wir uns die Berechnung, die wichtigsten Formeln sowie mehrere Beispiele dazu ansehen. Außerdem zeigen wir dir typische Werte für verschiedene Flächenpressungen, um dir einen ersten Eindruck zu vermitteln.
Wenn du dir das Lesen sparen möchtest, solltest du dir unser Video dazu anschauen!
Inhaltsübersicht
Flächenpressung Definition
Beim Aufeinanderdrücken der Festkörper stellt sich in der Kontaktfläche zwischen den Körpern eine Normallastverteilung ein. Die dadurch aufgebrachte Flächenpressung ist im Gegensatz zum aufgebrachten Druck nicht isotrop, also nicht zwingend konstant über die Kontaktfläche verteilt.
Sie hat eine Richtung und ist in Ihrer Lastverteilung zwar von der Höhe der Kraft F und der Flächengröße abhängig, aber auch von den Materialeigenschaften. Dazu gehören Eigenschaften wie z.B. die Oberflächenkontur oder die Form der Berührungsfläche. Es stellt sich eine charakteristische Spannungsverteilung ein. Das Spannungsmaximum befindet sich dabei nicht an der Körperoberfläche, sondern im Inneren der Körper. Die aufgebaute Spannung in den Körpern ist dabei eine wesentliche Ursache für die Entstehung von Pitting, also der Bildung von Grübchen in technischen Bauteilen.
Flächenpressung berechnen
Die Berechnung der Flächenpressung für linear-elastische Werkstoffe basiert auf der Halbraumtheorie. Bei linear-elastischen isotropen Werkstoffen kann sogar die hertzsche Pressung angewendet werden. Voraussetzung ist hier eine ebene und kleine Kontaktfläche, keine Schubspannungen und die Betrachtung der Körper als elastische Halbräume.
Bei komplexeren Körpergeometrien oder nichtlinearen Werkstoffen müssen andere Methoden eingesetzt werden. Ein bekanntes numerisches Berechnungsverfahren ist die Finite Elemente Methode, auch kurz FEM genannt. Mit Hilfe von Simulationen können hier visuelle Modelle der Verteilung der inneren Spannung an Bauteilen erstellt werden.
Flächenpressung Formel
Die Formel zur Berechnung in der Konstruktion lautet:
Dabei wird der Buchstabe p sowohl als Bezeichnung für den Druck, als auch für die Flächenpressung verwendet.
F ist die Kraft in Newton und A die Kontaktfläche der Köper. Diese wird normalerweisen in Quadratmeter oder in Quadratmillimeter angegeben. Ein Quadratmeter entspricht dabei 
Quadratmillimeter.
Flächenpressung Einheiten
Die Flächenpressung wird normalerweise in der Einheit Pascal angegeben. Ein Pascal entspricht dabei einem Newton pro Quadratmeter und ein Megapascal einem Newton pro Quadratmillimeter.
bzw. 
Mega steht dabei für den Umrechnungsfaktor zwischen den beiden Größen. Das heißt ein MPa entspricht 
. Üblicherweise werden die Flächen in Quadratmillimeter oder Quadratmeter angegeben, ansonsten musst du einfach umrechnen.
Zulässige Flächenpressung
Bauteile sollen in der Konstruktion so ausgelegt werden, dass sie der zulässigen Flächenpressung 
entsprechen. Es gilt:
Die zulässige Flächenpressung, auch Grenzflächenpressung genannt, wird dabei aus Werkstoffversuchen bestimmt. Diese ist maßgeblich von den Paarungseigenschaften der aufeinander einwirkenden Oberflächen abhängig. Sie kann in Tabellenwerken nachgeschlagen werden und beruht vor allem auf Erfahrungswerten.
Zulässige Flächenpressung Tabelle
Hier sehen wir einige ausgewählte Beispiele. Je nach Belastungsart (ruhend, schwellend, wechselnd) und Paarung (gleiche/verschiedene Werkstoffe) ergeben sich unterschiedliche Grenzflächenpressungen.
Bei ruhenden Wekstoffen und einer Paarung unterschiedlicher Werkstoffe wird hier immer die niedrigere Grenzflächenpressung gewählt. Also bei einer Paarung von beispielsweise Bronze und Stahl, müssen 30 MPA als zulässige Flächenpressung gewählt werden.
Flächenpressung Beispiel 1
Angenommen, ein Quader mit einer Länge von 30 cm aus Grauguss, drückt auf einen Stahlrahmen. Wie groß ist nun die maximal zulässige Kraft F?
Ein Umstellen der Gleichung ergibt:
Die zulässige Flächenpressung lesen wir aus der Tabelle ab.
Damit kann F bestimmt werden:
Wir erhalten eine maximal zulässige Kraft von 450 Kilonewton.
Flächenpressung Beispiel 2
In der dem zweiten Beispiel wollen wir die Flächenpressung für den Fall berechnen, dass die wirkende Kraft und die Flächen nicht senkrecht aufeinander stehen.
Die angreifende Kraft F beträgt hier 500 kN. Sie verteilt sich auf die Flächen A 
und B 
. Der Winkel alpha entspricht 15° und der Winkel ß 20°. Um nun die Flächenpressungen auf die Fläche A und die Fläche B zu berechnen, müssen wir zunächst die Kraft F in x und in y Richtung aufteilen. Es gilt:
Y-Richtung: 
X-Richtung: 
Nun kann die erste Gleichung nach 
aufgelöst werden und in die Zweite Gleichung einsetzt werden.
(1)
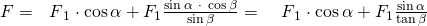(2)
Nun wird nach 
aufgelöst.
Die Flächenpressung ergibt sich also wie folgt:
Mit genau demselben Vorgehen wird auch 
ermittelt. Zunächst wird die x-Richtungsformel nach aufgelöst und in die Y-Gleichung eingesetzt. Wir erhalten:
Dann wird wiederum die Flächenpressungsformel angewandt.
Flächenpressung Anwendung
Die Flächenpressung ist vor allem bei der Auslegung und Dimensionierung von Schrauben, Zahnrädern, Wälzkörpern, Lagern, Stift- und Bolzenverbindungen eine wichtige Größe. Hier kann es bei einer zu großen Belastung durch Flächenpressung zu einem Versagen der Bauteile kommen. Deshalb müssen diese möglichst optimal dimensioniert werden.