Statischer Festigkeitsnachweis – Übung
Hallo! Du bist dir noch nicht ganz sicher, ob du das letzte Video verstanden hast? Jetzt zeigen wir dir anhand eines Beispiels, wie du den Festigkeitsnachweis in der Praxis anwendest.
Inhaltsübersicht
Welle mit Absatz auf Festigkeit überprüfen
In unserem Beispiel geht es um eine Welle mit Absatz, die auf ihre Festigkeit statisch überprüft werden soll. Die Welle ist aus dem Werkstoff E295 und ist somit ein Walzstahl. Sie unterliegt einem Biegemoment mit  sowie dem Torsionsmoment mit
sowie dem Torsionsmoment mit  . Der Durchmesser des Wellenabsatzes beträgt d=25mm.
. Der Durchmesser des Wellenabsatzes beträgt d=25mm.
Mindestsicherheit gegen Fließen
Du erinnerst dich sicher daran, dass es bei dem Festigkeitsnachweis darum geht, eine gewisse Mindestsicherheit gegen Fließen einzuhalten. Um zu wissen, wie groß diese ist, sehen wir in Tabelle 3-14 nach. Da unser Werkstoff ein Walzstahl ist, haben wir eine Mindestsicherheit von  . So, das hätten wir erst einmal geschafft. Als nächstes berechnen wir das Biege- und Torsionswiderstandmoment, da wir diese für unsere Spannungen brauchen. Da unsere Welle im Querschnitt einen Kreis ergibt, haben wir für das Biegewiderstandsmoment
. So, das hätten wir erst einmal geschafft. Als nächstes berechnen wir das Biege- und Torsionswiderstandmoment, da wir diese für unsere Spannungen brauchen. Da unsere Welle im Querschnitt einen Kreis ergibt, haben wir für das Biegewiderstandsmoment  und für das Torsionswiderstandsmoment
und für das Torsionswiderstandsmoment  .
.
Somit ergibt sich für unsere maximale Biegespannung:

und für die maximale Torsionsspannung:
 .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Biege- und Torsionsfließgrenze
Jetzt müssen wir noch die Biege- sowie Torsionsfließgrenze bestimmen und dann haben wir es schon fast geschafft. Dafür musst du aber zuerst den Korrekturfaktor  und die Dehngrenze
und die Dehngrenze 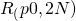 bestimmen. Aus Tabelle 1-1 erhältst du für den Werkstoff E295:
bestimmen. Aus Tabelle 1-1 erhältst du für den Werkstoff E295:  . Da der Wellen-Absatz einen Durchmesser von 25mm hat und wir uns nach der Streckgrenze eines Walzstahles richten, können wir aus Tabelle 3-11 den Wert
. Da der Wellen-Absatz einen Durchmesser von 25mm hat und wir uns nach der Streckgrenze eines Walzstahles richten, können wir aus Tabelle 3-11 den Wert  bei Linie 2 heraus lesen. Für die Biegung gilt also dann:
bei Linie 2 heraus lesen. Für die Biegung gilt also dann:

und für die Torsion:
 .
.
Wenn du das jetzt in die Formel für die Sicherheit gegen Fließen einsetzt, dann bekommst du auch schon deine vorhandene Sicherheit. Somit ergibt sich für  :
:
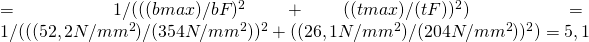
Da  ist und somit
ist und somit  ist, hält deine Welle die Belastung auf Biegung und Torsion aus und wird nicht brechen oder sich verformen.
ist, hält deine Welle die Belastung auf Biegung und Torsion aus und wird nicht brechen oder sich verformen.
So, wie du siehst ist das alles gar nicht so schwer. Wenn du den statischen Festigkeitsnachweis nach diesem Schema durchführst, dann kann nichts schiefgehen. Bis bald!


