DEA minimieren
Du hast einen deterministischen endlichen Automaten konstruiert und er ist extrem verwinkelt und umständlich? Kein Problem: du kannst einfach den DEA minimieren. Wir zeigen dir anhand eines Beispiels, wie du Schritt für Schritt zu einem Minimalautomat kommst.
Warum sollte man überhaupt einen DEA minimieren? Ganz einfach: es kann oft passieren, dass manche Zustände eines Automaten überhaupt nicht gebraucht werden und so den Automaten unnötig verkomplizieren.
Inhaltsübersicht
DEA minimieren – Beispiel
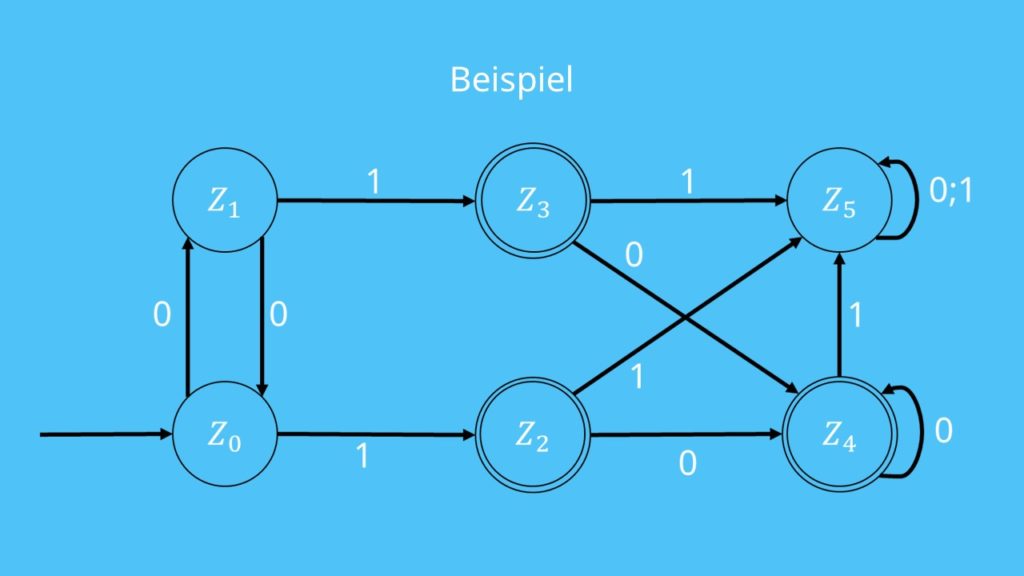
Schauen wir uns am besten an einem konkreten Beispiel an wie das Ganze funktioniert. Der deterministische endliche Automat für das Aufgabenbeispiel sieht als Zustandsübergangsdiagramm wie folgt aus:
Wir sehen, dass der Automat sechs Zustände und als Eingabealphabet die 0 und die 1 hat. Außerdem verfügt er über einen Start- sowie drei Endzustände. Wenn du damit noch Schwierigkeiten hast, schau dir doch zur Wiederholung unser Video zu deterministischen endlichen Automaten an.
Bei der Minimierung suchen wir nun alle Zustandspaare, die zu einem zusammengefasst werden können. Dafür erstellen wir uns zunächst eine Zustandspaartabelle mit allen möglichen Zustandspaaren. Hierbei ist es egal, ob die Zustände im Automaten verbunden sind oder nicht.
Zustände streichen
Jetzt beginnen wir Zustände zu streichen.
Da Zustände nicht mit sich selbst überprüft werden müssen, können wir die Diagonale der Tabelle komplett streichen. Außerdem werden die Paare nur in eine Richtung betrachtet, wir müssen die Paare (z1, z2) und (z2, z1) also nicht als einzelne Paare sehen und können damit die obere Hälfte der Tabelle über der Diagonalen (in der Abbildung rot markiert) streichen.
Die davon betroffenen Zustände sind hier grün markiert. Auch die neu markierten Zustände werden von uns gestrichen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Übergangstabelle
Als letztes werden die noch nicht markierten Zustandspaare auf alle möglichen Übergangsmöglichkeiten überprüft. Entsteht hierbei ein bereits gestrichenes Paar so wird das aktuell überprüfte Paar ebenfalls gestrichen.
Dies geschieht am einfachsten mit einer Übergangstabelle.
Wir testen jetzt für jedes Zustandspaar die Folgezustände bei der Eingabe der Zeichen 0 und 1. In der ersten Zeile wird Beispielsweise der Zustand z0 bei Eingabe einer 0 zu z1, während der Zustand z1 zu z0 wird. Dies wiederholen wir für alle leeren Zellen und erhalten folgende Tabelle:
Wir suchen uns nun die Zustandspaare, die bei einer Eingabe ein Zustandspaar ergeben, das bereits gestrichen ist. Ein Beispiel ist das Zustandspaar (z0, z5). Wird eine 1 eingegeben, dann entsteht das neue Zustandspaar (z2, z5). Wenn wir jetzt einen Blick in unsere Zustandspaartabelle werfen, sehen wir, dass dieses Paar bereits markiert ist. Wir finden insgesamt zwei solcher Paare, die jeweils bei einer Eingabe ein bereits markiertes Paar ergeben. Diese streichen wir dann wiederum in der Zustandspaartabelle.
Minimalautomat
Die übrig gebliebenen Paare können wir nun kombinieren.
Wir beginnen damit, das Paar (z0, z1) zu einem gemeinsamen Zustand z01 zu verschmelzen. Weiter geht es mit dem Paar (z2, z3), welches zum Zustand z23 wird. Versuchen wir nun dasselbe mit den Paaren (z2, z4) und (z3, z4), dann bemerken wir, dass jeweils ein Zustand bereits zu einem neuen Zustand verschmolzen wurde. Kein Problem, wir fügen die neuen Zustandspaare einfach an und erhalten den großen Zustand z234.
Vergleichen wir den Ausgangsautomaten mit dem Minimalautomat:
Wie du siehst, wurden mehrere Zustände des alten Automaten miteinander verschmolzen, was den Automaten deutlich einfacher aussehen lässt. Ein Beispiel ist, wenn du von den Zuständen z0 und z1 aus zwei-mal eine 0 beziehungsweise eine 1 eingibst: mit einer 0 bleiben beide Zustände im gleichen Zustand, und bei einer 1 landet man von beiden Zuständen aus im Zustand z5. Im Minimalautomat wurden daher z0 und z1 zusammengefasst, da sie sich gleich verhalten.
Einen DEA minimieren kannst du nun also auch! Der Algorithmus dauert zwar manchmal ein paar Minuten, aber das sollte man für einen komplett minimierten Automaten durchaus mal investieren!