Heap
Was ist ein Heap? Dieser Artikel behandelt die allgemeine Definition, sowie den Vergleich zwischen Stack und Heap Eigenschaften. Im nächsten Schritt wird die Heap-Bedingung erläutert, sowie der Unterschied zwischen einer Halde als Heap Baum oder als Array inklusive der Bedingungen Min-Heap und Max-Heap. Darauf aufbauend werden die Operationen Einfügen und Löschen erklärt. Zum Abschluss erfolgt ein Überblick zur Laufzeit.
Doch eigentlich willst du nur einen schnellen Überblick? Unser Video bringt alles, was du über die Bedingungen wissen musst und wie du Einfüge- und Lösch-Operationen in einer Baumstruktur vornehmen kannst. Zusätzlich zeigen wir dir dir an einem Beispiel den Speichervorgang im Array.
Inhaltsübersicht
Heap Speicher
Der Sinn und Zweck ist dabei die allgemeine Speicherung von Mengen. Dadurch können Heaps verschiedene Operationen unterstützen, wie beispielsweise das Einfügen und Entfernen von Elementen. Der Heap Speicher kann auch als dynamischer Speicher, Haldenspeicher oder Freispeichere bezeichnet werden. Er stellt im Allgemeinen einen Speicherbereich dar. Die darin gespeicherten Objekte können abgelegt und nach beliebiger Reihenfolge wieder freigegeben werden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Heap vs Stack
Ein Stack (deutsch Stapel) arbeitet nach dem LIFO-Prinzip (Last in – First Out). Somit werden die Daten aufeinandergestapelt gespeichert und können danach nur von oben nach unten entfernt werden. Wenn man nun also Heap vs Stack vergleicht, zeigt der Haufen eine deutlich unstrukturiertere Form auf.
Stack Eigenschaft
Die Stack Eigenschaften im Überblick:
- Fixe Größe
- LIFO-Prinzip
- Speicherung von Information zum Programmablauf und lokalen Variablen
- Effizientes Ablegen und Entfernen von Objekten
- Keine Freigabe des Speichers
Heap Eigenschaft
Die Heap Eigenschaften im Überblick:
- Flexible Größe bis zur Speichergrenze auf Prozessebene
- Durch schwierige interne Verwaltung, Anlegen und Entnehmen langsamer
- Ohne Garbage Collector manuelle Freigabe des Speichers
Heap Baum
Eine Halde lässt sich sowohl als Baum darstellen als auch als Array. Ein Binärer Heap besteht dabei beispielsweise aus einem Binärbaum . Jeder Knoten darf also höchstens zwei Kinder haben. Der Haufen wächst – wie bei Baumstrukturen meistens – von der Wurzel aus nach unten und von links nach rechts.
Min-Heap
Der Min-Heap zeichnet sich durch die Eigenschaft aus, dass der Elternknoten immer kleiner oder gleich der Kindknoten ist. Durch diese Bedingung ist immer ein Objekt mit dem minimalsten Schlüssel als Wurzel im Baum zu finden.
Max-Heap
Beim Max-Heap ist die Bedingung genau andersherum: Die Werte in den Kindknoten müssen stets kleiner oder gleich denen der Elternknoten sein. Dadurch ist die Bedingung, dass die Wurzel des Baums das Element mit dem maximalen Schlüssel darstellt.
Operationen
Heaps unterstützen je nach Art verschiedene Formen von Operationen:
- Insert: Einfügen von Objekten und Elementen
- Remove: Entfernen von Objekten und Elementen
- ExtractMin: Rückgabe von Objekten und Elementen mit minimalem Schlüssel
- ChangeKey: Anpassen von Schlüsseln
- DecreaseKey: Verkleinerung von Schlüsseln
- Merge: Verschmelzung von zwei Haufen
Einfügen
Als Beispiel dient ein Baum, der nach dem Min-Prinzip aufgebaut ist.
Wenn in diesem Baum die Zahl die 26 einfügt werden soll, dann muss die Zahl entsprechend unseres Schemas von links nach rechts in den Baum eingesetzt werden. Die Bedingung ist dadurch weiterhin erfüllt.
Wenn nun zusätzlich noch die 10 einfügt wird, dann ist sein Elternknoten – die 12 – größer und verletzt die Bedingung. Dieses Problem löst sich, indem die beiden Knoten vertauscht werden. Schon ist es wieder eine korrekte Halde.
Wenn man nun noch die 3 einfügt, muss man sie nicht nur mit der 15 tauschen, sondern im nächsten Schritt auch noch mit der 6.
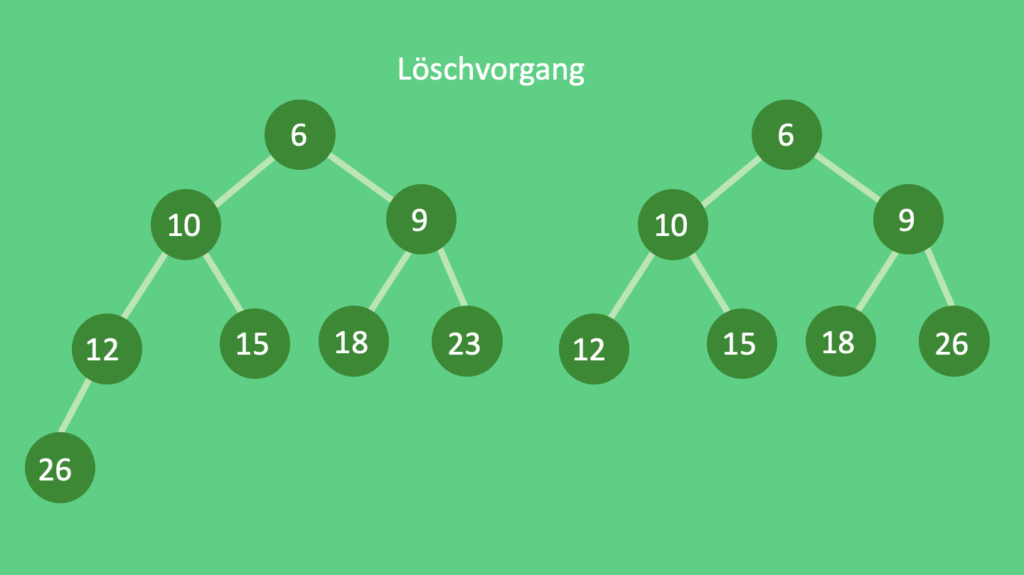
Löschen
Der Löschvorgang verhält sich bei beiden Bedingungen gleich. Gegeben sei wiederrum ein Min-Heap Beispiel und im ersten Schritt wird die Wurzel 2 gelöscht.
Dafür entfernt man die 2 zuerst aus dem Haufen und fügt sie in einen Speicher ein. Die Wurzel ist damit erstmal leer und wird mit einem anderen Wert gefüllt.
Man verwendet hierbei das letzte Element aus dem Haufen und setzt es dann als neue Wurzel ein! Danach findet ein mehrmaliger Tauschvorgang mit den kleineren Kindknoten statt bis wieder ein gültiger Haufen gegeben ist.
Als nächstes entfernt man noch die 23. Da der Baum stets von oben nach unten und von links nach rechts aufgebaut werden soll, muss man die dritte Ebene wieder mit der 26 auffüllen.
Array
Ein Haufen lässt sich auch als Array darstellen. Dafür gilt im Allgemeinen dieses Rechen-Schema:
Die Wurzel kommt dabei immer direkt in die nullte Speicherzelle unseres Arrays. Und der Rest ist ganz einfach: Man nummeriert den Baum von oben nach unten und von links nach rechts.
Der linke Kindknoten der Wurzel wird in der ersten Zelle gespeichert und der rechte in der Zweiten.
Nach diesem Schema kann nun der komplette Baum in einem Array abgespeichert werden:
| Element | 2 | 6 | 9 | 10 | 15 | 18 | 23 | 12 | 26 |
| Speicherzelle | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Komplexität
Die Laufzeit der Haufen ist von der jeweils durchgeführten Operation und ihrer Art abhängig. Die Laufzeiten für den Binären und Binomiale Form sind:
- Insert:

- Remove:

- ExtractMin:

- ChangeKey:

- DecreaseKey:

Anwendung
Eine häufige Anwendung finden Haufen in Form von Prioritätswarteschlangen zur Festlegung einer Reihenfolge zur Ausführung von Aufgaben. Zusätzlich bieten sie für einen Greedy-Algorithmus eine ideale Datenstruktur. Zusätzlich sorgt ein Binärer Heap für die Sortierung eines Heapsort .