Binärbaum
Der folgende Beitrag beschäftig sich rund um die Binärbäume, der an der häufigsten verwendeten Art der Bäume in der Informatik. Gestartet wird mit der allgemeinen Terminologie. Darauf aufbauen wird die Binärbaum Höhe, Tiefe und Größe definiert. Danach werden die speziellen Arten partiell geordneter Baum und vollständiger Binärbaum vorgestellt. Anhand eines Beispiels wird die Binärbaum Traversierung erläutert. Zum Abschuss erfolgt ein exemplarischer Quellcode in Java.
Inhaltsübersicht
Binäre Bäume – Terminologie
Binärbäume stellen eine spezielle Form von Graphen dar. In der Graphentheorie stellen sie im Allgemeinen einen Baum dar, welcher bei jedem Knoten immer höchstens zwei Nachkommen besitzen darf.
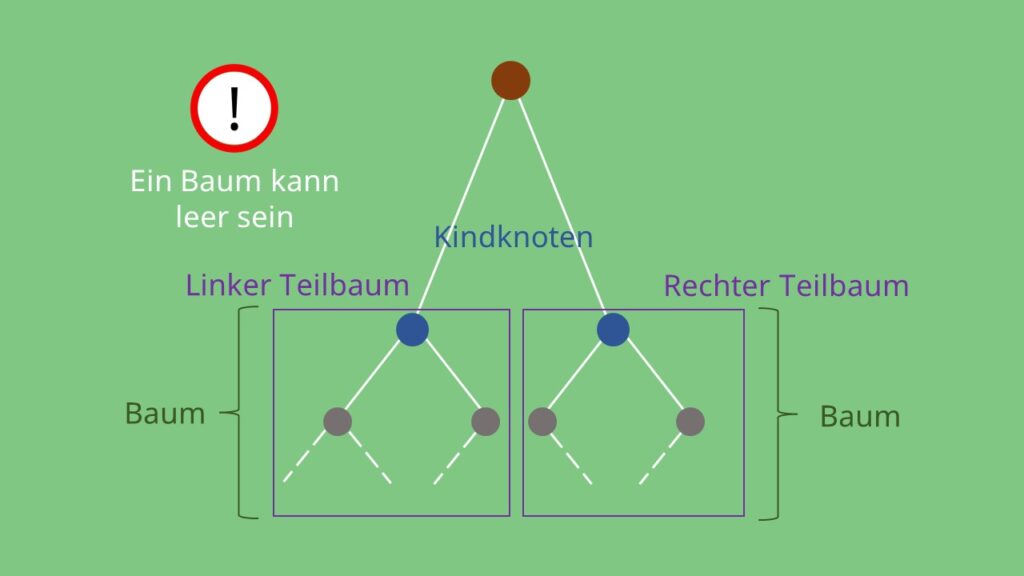
Ein binärer Baum kann entweder leer sein oder er besteht aus einer Wurzel, sowie einem linken und einem rechten Teilbaum. Diese Teilbäume sind wiederrum selbst binäre Bäume.
Meistens werden Binärbäume als Out-Trees angesehen. Dabei hat die Wurzel einen Eingangsgrad von 0 und die Kindknoten einen Eingangsgrad 1. Der Ausgangsgrad bezeichnet die Anzahl der Kindknoten. Da diese bei Binärbäumen höchstens zwei sein dürfen, bezeichnet man die Ordnung als Out-Tree kleiner-gleich 2. Dabei sind Knoten mit einem Ausgangsgrad größer-gleich 1 innere Knoten, Knoten mit einem Ausgangsgrad von 0 sind wiederrum Blätter/äußere Knoten.
Zusätzlich können Binärbäume als Besonderheit auch ein sogenanntes Halbblatt besitzen, was eigentlich nur einen Knoten mit Ausgangsgrad 1 bezeichnet, wodurch ein Blatt zu einem doppelten Halbblatt wird.
Binärbaum Höhe, Tiefe und Größe
- Tiefe: Die Tiefe eines Knotens bezeichnet die Anzahl aller gerichteten Kanten bis zur Wurzel.
- Größe: Die Gesamtzahl der Knoten ergeben die Größe eines Baums.
- Höhe: Die Höhe einer Wurzel definiert in diesem Zusammenhang die Höhe des Baums und auch die Tiefe des Baums. Die Höhe eines Knotens beschreibt den längsten Weg, den man von diesem Knoten aus gehen kann. Dafür können die Knoten in sogenannte Stufe (englisch level) eingeteilt werden. Alle Knoten, die horizontal gleichhoch sind, gehören dabei zur selben Stufe. Die maximale Stufe minus 1 ergeben dann im häufigsten Fall die Baumhöhe, jedoch zählen ab und an Autoren zu der Höhe eine 1 dazu.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Partiell geordneter Baum
Ein partiell geordneter Baum stellt eine spezielle Form eines binären Baums dar. Er zeichnet sich durch die folgenden Eigenschaften aus:
- Seine Knoten sind markiert.
- Diese Markierungen stammen aus einem geordneten Wertebereich.
- Alle Knoten aus jedem Teilbaum sind größer markiert als die Wurzel oder sind gleich der Wurzel.
Heißt also, dass der Wert eines Knotens immer größer oder kleiner als die Werte seiner Nachfolger ist. Ein solcher partiell geordneter Baum kann beispielsweise so aussehen:
Vollständiger Binärbaum
Ein vollständiger Binärbaum zeichnet sich dadurch aus, dass alle seine Blätter die gleiche Tiefe haben.
Das bedeutet, dass ein vollständiger Binärbaum sich dadurch auszeichnet, dass alle Knoten so viele Nachfolger besitzen, wie es maximal möglich ist.
Zusätzlichen gehören zu den binären Bäumen auch ein binärer Suchbaum , der AVL-Baum oder auch der Rot-Schwarz-Baum.
Binärbaum Traversierung
Oft möchte man Binärbäume als Text ausgeben. Dieser Vorgang nennt sich traversieren. Die Binärbaum Traversierung bezeichnet dabei das systematische Untersuchen von den Knoten eines Baumes in einer bestimmten Reihenfolge. Je nachdem, in welcher Reihenfolge die Knoten abgearbeitet werden, ergibt sich eine andere Textausgabe. In diesem Beispiel erfolgt die Traversierung nach dem depth-first-Prinzip, also der Tiefensuche (inorder, preorder, postorder) und breadth-first.
Preorder
Die Ausgabe des Preorder-Verfahrens ordnet sich wie folgt:
- Wurzel
- Linker Teilbaum
- Rechter Teilbaum
Nach unserem Beispiel ergibt sich für den Preorder Baum die folgende Ausgabe:
20, 10, 5, 15, 30, 25, 35
Postorder
Eine Ausgabe eines Postorder Baums baut sich folgendermaßen auf:
- Linker Teilbaum
- Rechter Teilbaum
- Wurzel
Die Ausgabe des Beispiels lautet Postorder:
5, 15, 10, 25, 35, 30, 20
Inorder
Bei der Inorder Traversierung erfolgt die Reihenfolge der Ausgabe nach dem folgenden Prinzip:
- Linker Teilbaum
- Wurzel
- Rechter Teilbaum
Der Inorder Baum erhält dieses Ergebnis als Ausgabe:
5, 10, 15, 20, 25, 30, 35
Level-order
Zusätzlich ist auch eine breadth-first/ Breitensuche möglich. Dieses Verfahren wird oft auch level-order genannt. Dabei wird bei der Ausgabe mit der Baumwurzel begonnen und dann die einzelnen Ebenen von links nach rechts durchlaufen.
Für das Beispiel ergibt sich dann diese Ausgabe:
20, 10, 30, 5, 15, 25, 35
Binärbaum Java
Ein Binärbaum Java Beispiel kann sich exemplarisch wie folgt aufbauen:
class Binaerbaeume
{ Binaerbaum links;
Binaerbaum rechts;
int inhalt;
Binaerbaeume (int zahl)
{ this.links = null;
this.rechts = null;
this.inhalt = zahl;
}
void einfuegen (int wert)
{ if (wert < inhalt)
{
if (links == null)
links = new Binaerbaeume(wert);
else links.einfuegen(wert);
}
else {
if (rechts == null)
rechts = new Binaerbaeume(wert);
else rechts.einfuegen(wert);
}
}
void laufeDurch ()
{ if (links != null) links.laufeDurch();
Out.print(inhalt); Out.println();
if (rechts != null) rechts.laufeDurch();
}
}
class Binaerbaeume
{
static Binaerbaeume baum;
public static void main(String[] arg)
{ int wert = 0;
String i;
boolean baumErstellen = false;
Out.print(„Hier bitte Werte eingeben. Ende mit -1.“); Out.println();
while (wert != -1)
{ Out.print(„Bitte Wert eingeben: „);
wert = In.readInt();
i = In.readLine();
if (!baumErstellen)
{ baum = new Binaerbaeume(wert);
baumErstellen = true;
}
else {
baum.einfuegen(wert);
}
}
baum.durchlaufen();
}
}