Video anzeigen

Hier geht's zum Video „Volumenstrom“

Hier geht's zum Video „Strömungsgeschwindigkeit berechnen“

Hagen Poiseuille Gesetz

Wichtige Inhalte in diesem Video

Hagen Poiseuille Gesetz einfach erklärt

Gesetz von Hagen-Poiseuille

Herleitung Hagen-Poiseuille Gesetz

Geschwindigkeitsprofil

Das Gesetz von Hagen-Poiseulle ist zur Berechnung des Volumenstroms notwendig, wenn innere Reibung vorliegt. Vor allem bei laminare Strömungen ist das der Fall. In diesem Beitrag wird auf die genaue Berechnung eingegangen.

Haben wir dein Interesse geweckt und du möchtest diese Thematik in Bild und Ton angehen? Dann schau dir unser Video an, darin erklären wir dir alles!

Inhaltsübersicht

Hagen Poiseuille Gesetz einfach erklärt

im Videozur Stelle im Video springen

Merke

Das nach dem deutschen Ingenieur G. Hagen und dem französischen Physiker J.L.M. Poiseuille benannte Gesetz, beschreibt den Volumenstrom in sehr dünnen Röhrchen unter bestimmten Voraussetzungen. Die Strömung muss dabei ein laminares stationäres Verhalten aufweisen und das Medium muss die Eigenschaften eines newtonschen Fluids (z.B. Wasser) besitzen.

Das Gesetz findest du sowohl in der Strömungslehre als auch in der Medizin. Stell dir vor, eine Flüssigkeit strömt ohne Krafteinwirkung durch ein enges Röhrchen und wird mit der Zeit aufgrund von Reibungskräften immer langsamer bis hin zum Stillstand. Herrscht nun aber eine Druckdifferenz zwischen dem Ein- und Ausgang des dünnen Röhrchens, beginnt es wieder zu fließen – und zwar in Richtung des niedrigeren Drucks. Den Zusammenhang zwischen der Viskosität, dem Radius und der Länge des Rohres und der Druckdifferenz wird in dem Gesetz beschrieben. Um das Gesetz mathematisch zu definieren betrachtest du alle auftretenden Kräfte und stellst die Verbindung zu den einzelnen Faktoren auf.

Gesetz von Hagen-Poiseuille

im Videozur Stelle im Video springen

Nachdem wir ja jetzt wissen, was dieses Gesetz beschreibt stellen wir uns die Frage, wozu man es überhaupt benötigt. Das Hagen Poiseuille Gesetz ist auf einen Gültigkeitsbereich für alle Geschwindigkeiten in engen Röhrchen beschränkt. Dazu zählt vor allem die Kapillare, beziehungsweise die Kapillaren, also sehr enge Röhrchen.

Außerdem war das Hagen Poiseuille Gesetz für die Erforschung des Reibungsgesetztes in strömenden Flüssigkeiten von essentieller Bedeutung, da sich die Reibungskraft durch ein Experiment sehr genau nachprüfen lässt.

Zusätzlich bietet es die Möglichkeit, eine Verengung des Röhrchens durch eine exakt berechnete Druckerhöhung zu kompensieren. Dafür wird die Grundformel des Hagen Poiseuille Gesetztes auf die Druckdifferenz umgestellt. Damit jedoch die notwendige Druckerhöhung berechnet werden kann muss sowohl die Berechnung vor, als auch nach der Verengung erfolgen. Danach ergibt die Differenz der beiden Druckunterschiede den notwendigen Druck.

$\dot{V}=\frac{\pi\cdot r^4}{8\cdot \eta}\cdot \frac{\mathrm{\Delta} p}{l} \Rightarrow \mathrm{\Delta} p=\frac{\dot{V}\cdot 8\cdot\eta\cdot l}{\pi\cdot r^4}$

Herleitung Hagen-Poiseuille Gesetz

im Videozur Stelle im Video springen

In den folgenden Absätzen findest du eine schrittweise beschriebene Herleitung für das Gesetz von Hagen Poiseuille.

Impulsbilanz

im Videozur Stelle im Video springen

Für die Herleitung des Hagen Poiseuille Gesetzes erfolgt die Betrachtung eines Zylinders mit dem Radius und einer infinitesimal kleinen Höhe . Dieser liegt gedanklich in einem durchströmten Rohr. An diesem Zylinder wird die Impulsbilanz aufgestellt.

Hagen Poiseuille Gesetz, Impulsbilanz, Kräftebilanz — Hagen Poiseuille Gesetz Impulsbilanz

Da die Impulsströme die Dimension einer Kraft haben, handelt es sich um ein Kräftegleichgewicht. Vorhanden sind die beiden Druckkräfte $p(x)r^2\pi$ und $-p(x+dx)r^2\pi$ auf den Stirnflächen des Zylinders und die Reibungskraft $\tau(r)2r\pi dx$ . Diese werden gleichgesetzt und es ergibt sich das Kräftegleichgewicht.

$p(x)r^2\pi-p(x+dx)r^2\pi=\tau (r)2r\pi dx$

Dieses Gleichgewicht lässt sich für den nächsten Schritt umformen in

$\tau (r)=\frac{r}{2}\cdot \frac{p(x+dx)-p(x)}{dx}=\frac{r}{2}\cdot \frac{dp}{dx}$

Geschwindigkeitsprofil

im Videozur Stelle im Video springen

Mit der Definition der Schubspannung eines newtonsches Fluid $\tau (r)=\eta\cdot \frac{du}{dr}$ und der darin vorhandenen axialen Geschwindigkeit u(r) lässt sich das Geschwindigkeitsprofil definieren. Und dabei fällt auch sofort die Abhängigkeit von der Viskosität der Flüssigkeit auf.

$\eta\cdot\frac{du}{dr}=\frac{r}{2}\cdot\frac{dp}{dx}\Leftrightarrow\frac{du}{dr}=\frac{dp}{dx}\cdot\frac{r}{2\eta}$

Die Lösung der Differentialgleichung lautet

$u(r)=\frac{dp}{dx}\cdot\frac{r^2}{4\eta}+C$

Als nächster Schritt muss die Konstante hergeleitet werden. Bei erreicht der Radius die Rohrwand, weswegen die Randbedingung r=R gilt. An diesem Punkt ist die Geschwindigkeit der Teilchen gleich Null und es bildet sich keine Diskontinuitätsfläche. Deswegen wird das Geschwindigkeitsprofil gleich Null gesetzt und die Konstante ausgerechnet.

$u(R)=\frac{R^2}{4\eta}\cdot\frac{dp}{dx}+C=0 \Leftrightarrow C=\left(-\frac{dp}{dx}\right)\cdot\frac{R^2}{4\eta}$

Setzt man die Konstante nun wieder in das Geschwindigkeitsprofil u(r) lässt sich die Gleichung folgendermaßen auflösen und umformen

$u(r)=\left(-\frac{dp}{dx}\right)\cdot\frac{R^2}{4\eta}\cdot \left(1-\left(\frac{r}{R}\right)^2\right)$

Da das Gesetz von Hagen-Poiseuille von dem Volumenstrom handelt muss dieser letztendlich berechnet beziehungsweise definiert werden. Um mehr zum Volumenstrom zu erfahren haben wir hier das passende Video für dich. Dazu benötigt man zuerst die allgemeine Formel des Volumenstroms in diesem Betrachtungsfall.

Volumenstrom

im Videozur Stelle im Video springen

Diese ergibt sich aus der Integrationsformel der Querschnittsfläche des Rohres $A=\int_{0}^{R}2r\pi dr$ und dem Geschwindigkeitsprofil u(r) .

$\dot{V}=\int_{0}^{R}u(r)2r\pi dr$

Jetzt kann die Formel für das Geschwindigkeitsprofil u(r) eingesetzt und die endgültige Formel für den Volumenstrom $\dot{V}$ hergeleitet werden.

$\dot{V}=\int_{0}^{R}\left(-\frac{dp}{dx}\right)\cdot\frac{R^2}{4\eta}\cdot\left(1-(\frac{r}{R})^2\right)2r\pi dr=\left(-\frac{dp}{dx}\right)\cdot \frac{r^2\pi}{2\eta}\cdot\int_{0}^{R}\left(r-\frac{r^3}{R^2}\right)dr$

$=\left(-\frac{dp}{dx}\right)\cdot\frac{R^2\pi}{2\eta}\cdot\Bigl\langle\frac{r^2}{2}-\frac{r^4}{4R^2}\Bigr\rangle_{0}^{R}=\left(-\frac{dp}{dx}\right)\cdot\frac{R^2\pi}{2\eta}\cdot\Bigl\langle\frac{R^2}{2}-\frac{R^4}{4}\Bigr\rangle_{0}^{R}$

Es ergibt sich folgende Gleichung.

$\dot{V}=\left(-\frac{dp}{dx}\right)\cdot\frac{R^4\pi}{8\eta}$

Als letzten Aspekt erfolgt die Umformung des Druckgradienten 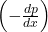$\left(-\frac{dp}{dx}\right)$ in einen Faktor, mit dem letztendlich auch gerechnet werden kann.

Dabei wird auf die Definition des Druckverlusts entlang einer Rohrstrecke zurückgegriffen

$\mathrm{\Delta}p=l\cdot\left(-\frac{dp}{dx}\right)$

Dadurch ergibt sich die finale Gleichung für das Gesetz von Hagen-Poiseuille wie folgt:

$\dot{V}=\frac{\pi\cdot r^4}{8\cdot \eta}\cdot \frac{\mathrm{\Delta} p}{l}$

Die Volumenstromberechnung ist dementsprechend abhängig von dem Radius und der Länge des Rohres , des Druckverlusts und der Viskosität der Flüssigkeit.

Formulierung und Einheit

Die Herleitung sieht schon etwas komplizierter aus. Deswegen gehen wir jetzt noch etwas genauer auf die eigentliche Formulierung des Gesetzes ein.

Wir haben bereits gesagt, dass die Volumenstromberechnung über das Gesetz von Hagen Poiseuille abhängig von mehreren Faktoren ist. Das sind der Radius des Rohres, der Länge des Rohres, der Druckunterschied $\mathrm{\Delta}p$ zwischen Beginn und zum Ende des Rohres und die Viskosität $\eta$ des Fluids. Besonders hervorzuheben ist die vierfache Potenz des Radius. Dies hat zur Folge, dass bereits eine Halbierung des Radius den Volumenstrom um das 16-fache reduziert. Aufgrund dieses Zusammenhangs ist dieser Aspekt im Bereich der Medizin kritisch. Du kannst diese Analogie auf die Adern übertragen und dir vorstellen, was passiert wenn deren Radius beispielsweise durch Verkalkung verringert wird. Der Blutdruck erhöht sich durch den erhöhten Aufwand der Pumpleistung des Herzens und birgt große Gefahr für die Gesundheit.

Nach der Herleitung und Definition fehlt noch die Betrachtung der SI-Einheit. Diese basiert auf der Definition des Volumenstroms als Volumen pro Zeit und besitzt dementsprechend die Einheit

$\dot{V}=\frac{m^3}{s}$

Hagen Poiseuille und das Ohmsche Gesetz

Siehst du dir die Formel für das Hagen Poiseuille Gesetz genauer an, kannst du eine Analogie zum Ohmschen Gesetz feststellen. Um das besser zu erkennen kann man die Formel etwas umstellen, sodass die Druckdifferenz einzeln vorkommt.

$\dot{V}=\frac{\pi\cdot r^4}{8\cdot \eta\cdot l}\cdot \mathrm{\Delta} p}$

Dabei ist der Faktor 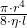$\frac{\pi\cdot r^4}{8\cdot \eta\cdot l}$ der Strömungsleitwert, was nichts anderes als eine Analogie des Kehrwerts zum Widerstand in der Elektrotechnik ist. Es gilt also

$R=\frac{8\cdot \eta\cdot l}{\pi\cdot r^4}$

Somit ist auch klar, dass der Volumenstrom der elektrischen Stromstärke und die Druckdifferenz der elektrischen Spannung entspricht.

Das Ohmsche Gesetz wird definiert als

$R=\frac{U}{I}$

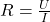
und stellt somit die Basis für folgende Gleichsetzung.

$\dot{V}=\frac{\pi\cdot r^4}{8\cdot \eta\cdot l}\cdot \mathrm{\Delta} p}\Leftrightarrow I=\frac{U}{R}$

Etwas übersichtlicher dargestellt gilt folgendes:

$\dot{V}=I$

$\mathrm{\Delta} p=U$

$\frac{\pi\cdot r^4}{8\cdot \eta\cdot l}=\frac{1}{R}$

Archimedisches Prinzip

Hydrostatischer Druck

Hydrostatik - Druck in ruhender Flüssigkeit

Hydrostatik - Druck in bewegter Flüssigkeit

Laminare und turbulente Strömung

Dynamik von Fluiden - Impulssatz

Strömung mit Reibung

Navier Stokes Gleichung

Hagen Poiseuille Gesetz

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .