Pol-Nullstellen-Plan
Für deine Prüfung sollst du einen Pol-Nullstellen-Plan erstellen, aber alles was dir dazu einfällt ist, dass du Null Plan davon hast? Wir ändern das! Lies dir einfach unseren Beitrag dazu durch, oder schau dir hier unser Video an!
Inhaltsübersicht
Erstellung des Pol-Nulstellen-Plans
Einen Pol-Nullstellen-Plan nutzt du, um Aussagen über gewisse Systemeigenschaften zu treffen. Darunter fallen zum Beispiel die Stabilität oder die Schwingungsfähigkeit. Wie der Name schon vermuten lässt, ist dieser Plan wie eine Landkarte, auf der du Pole und Nullstellen der Übertragungsfunktion einträgst.
Das Ganze wird in der komplexen Ebene aufgetragen. Die x-Achse beschreibt dabei den Realteil und die y-Achse den Imaginärteil der Funktion. Als Markierungen für Nullstellen wählt man kleine Kreise; für Pole zeichnest du ein kleines x.
Sehen wir uns ein Beispiel an:
Wir haben eine Übertragungsfunktion
 gegeben.
gegeben.
Um unseren Pol-Nullstellen-Plan aufzustellen, müssen wir die Pole bestimmen und G von S nach S auflösen.
Wir erhalten zwei Lösungen:
Zur Erinnerung: In der komplexen Ebene erhält der Imaginärteil die Zahl i und der Realteil die Zahl j. Die Imaginärachse teilt die komplexe Ebene außerdem in zwei Teile. Die linke Seite nennt man „linke komplexe Halbebene“ und die rechte heißt „rechte komplexe Halbebene“.
Die beiden Lösungen für S kannst du jetzt in das Koordinatensystem eintragen, indem du für den x-Wert minus Einhalb wählst und für die y-Werte jeweils plus beziehungsweise minus Wurzel 3 durch zwei.
Um eine Aussage über die Stabilität eines Systems zu treffen, sieht man sich die Lage der Pole an.
Asymptotisch stabile Systeme
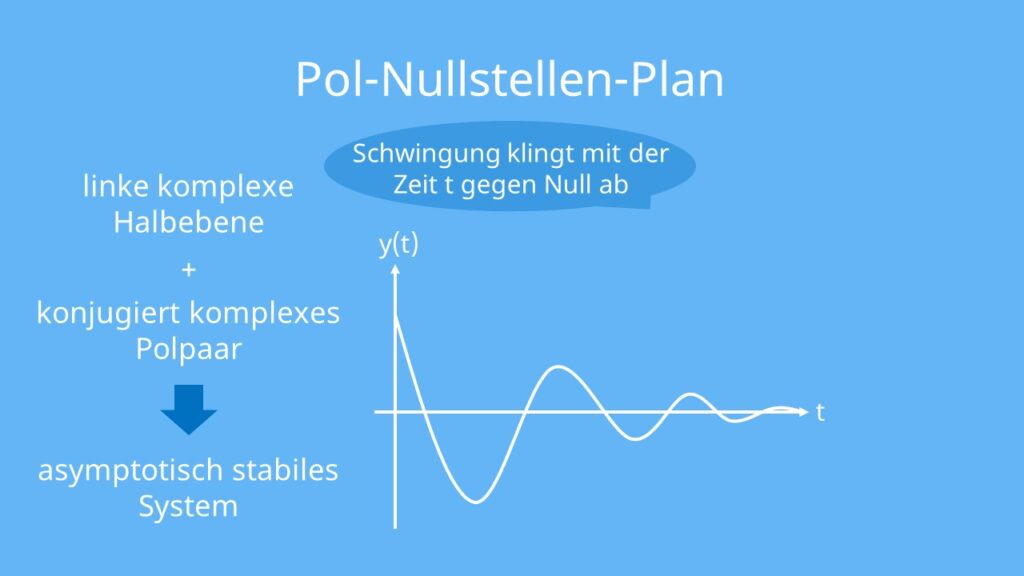
In unserem Beispiel liegen beide in der linken komplexen Halbebene. Befinden sich beide genau übereinander, spricht man von einem konjugiert komplexen Polpaar. Mit den Informationen „linke komplexe Halbebene und konjugiert komplexes Polpaar“, gelangst du zu dem Schluss, dass das System „asymptotisch stabil“ ist. In Worten: Wird das System in irgendeiner Weise angeregt oder ausgelenkt, so klingt seine Schwingung mit fortschreitender Zeit gegen Null ab. Dieses Zeitverhalten kannst Du grafisch so zeichnen:
Als Eselsbrücke kannst du dir bei den Pol-Nullstellen-Plänen immer ein Pendel vorstellen, das du auslenkst und das sich entweder einpendelt oder immer weiter schwingt!
Ein System ist auch dann asymptotisch stabil, wenn beide Pole nebeneinander auf der reellen Achse liegen. Das Zeitverhalten skizziert sich dann ein wenig anders:
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Grenzstabile Systeme
Es gibt Systeme, die man als „grenzstabil“ bezeichnet. Dafür müssen die Pole der Übertragungsfunktion in der linken komplexen Halbebene oder auf der imaginären Achse liegen. Befinden sie sich auf dieser Achse, dürfen die Pole allerdings nicht doppelt sein. Das heißt, dass es keine doppelten Lösungen für ein S geben darf! Die beiden Fälle sehen im Pol-Nullstellen-Plan mit jeweiligem Zeitverhalten so aus:
Das System klingt hier mit der Zeit also nicht gegen Null ab, sondern bleibt in endlichen Grenzen, die seine Schwingung eingrenzen.
Instabile Systeme
Die dritte Gruppe bilden die instabilen Systeme. Denkst du an das Pendel, musst du dir das so vorstellen: Du lenkst das Gewicht am Ende des Fadens um einen Winkel, zum Beispiel fünfzehn Grad aus. Anstatt sich mit der Zeit in die Richtung der Ruheposition einzupendeln und den Winkel somit immer weiter zu verkleinern, schwingt dein Pendel immer weiter und weiter und vergrößert seinen Winkel sogar noch ins Unendliche!
Diesen Fall hast du vorliegen, wenn mindestens ein Pol der Übertragungsfunktion in der rechten komplexen Ebene oder ein mehrfacher Pol auf der imaginären Achse liegt.
Das Zeitverhalten zeigt diese Bewegung ins Unendliche auch ganz deutlich.
Zum Abschluss gibt’s noch eine kleine Übersicht, mit der du für deine Prüfung bestens gewappnet bist und die auch platzsparend aufs Formelblatt passt!
So schnell wird aus Null Plan, Pol-Nullstellen-Plan! Viel Erfolg bei deiner Klausur!